Dirk Ormoneit
Lattice Particle Filters
Jan 10, 2013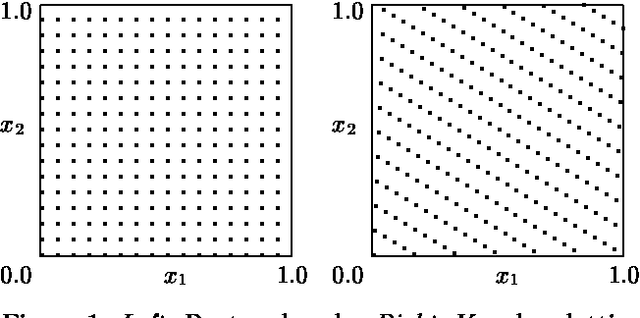
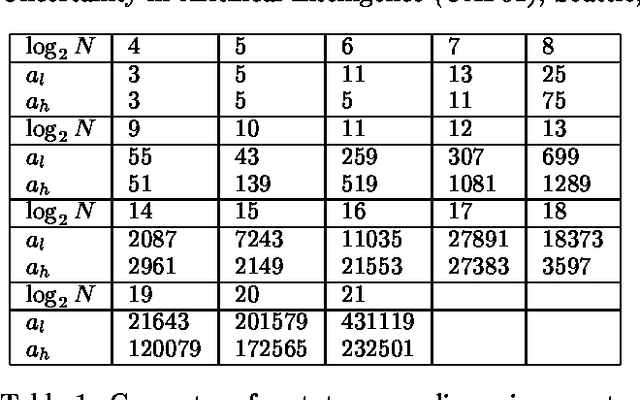
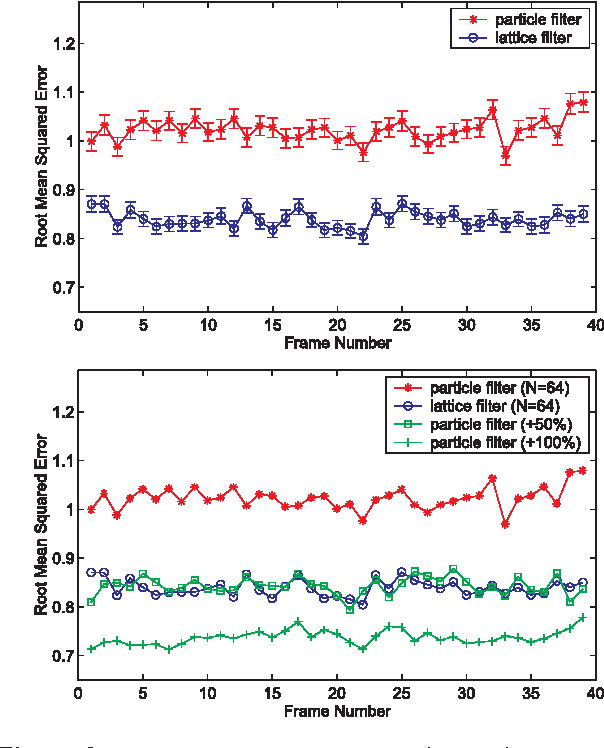

Abstract:A standard approach to approximate inference in state-space models isto apply a particle filter, e.g., the Condensation Algorithm.However, the performance of particle filters often varies significantlydue to their stochastic nature.We present a class of algorithms, called lattice particle filters, thatcircumvent this difficulty by placing the particles deterministicallyaccording to a Quasi-Monte Carlo integration rule.We describe a practical realization of this idea, discuss itstheoretical properties, and its efficiency.Experimental results with a synthetic 2D tracking problem show that thelattice particle filter is equivalent to a conventional particle filterthat has between 10 and 60% more particles, depending ontheir "sparsity" in the state-space.We also present results on inferring 3D human motion frommoving light displays.
Robust Combination of Local Controllers
Jan 10, 2013



Abstract:Planning problems are hard, motion planning, for example, isPSPACE-hard. Such problems are even more difficult in the presence of uncertainty. Although, Markov Decision Processes (MDPs) provide a formal framework for such problems, finding solutions to high dimensional continuous MDPs is usually difficult, especially when the actions and time measurements are continuous. Fortunately, problem-specific knowledge allows us to design controllers that are good locally, though having no global guarantees. We propose a method of nonparametrically combining local controllers to obtain globally good solutions. We apply this formulation to two types of problems : motion planning (stochastic shortest path) and discounted MDPs. For motion planning, we argue that usual MDP optimality criterion (expected cost) may not be practically relevant. Wepropose an alternative: finding the minimum cost path,subject to the constraint that the robot must reach the goal withhigh probability. For this problem, we prove that a polynomial number of samples is sufficient to obtain a high probability path. For discounted MDPs, we propose a formulation that explicitly deals with model uncertainty, i.e., the problem introduced when transition probabilities are not known exactly. We formulate the problem as a robust linear program which directly incorporates this type of uncertainty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge