Lattice Particle Filters
Paper and Code
Jan 10, 2013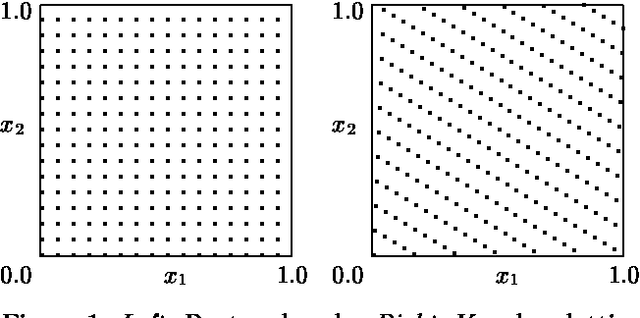
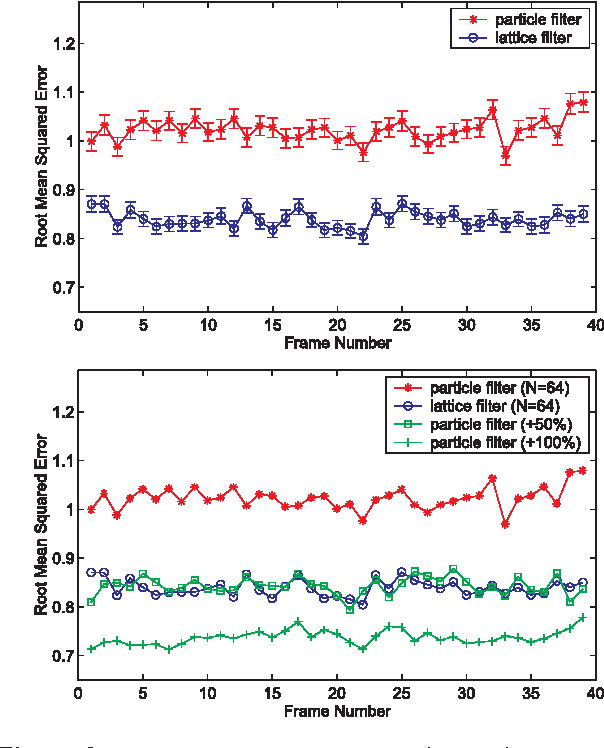

A standard approach to approximate inference in state-space models isto apply a particle filter, e.g., the Condensation Algorithm.However, the performance of particle filters often varies significantlydue to their stochastic nature.We present a class of algorithms, called lattice particle filters, thatcircumvent this difficulty by placing the particles deterministicallyaccording to a Quasi-Monte Carlo integration rule.We describe a practical realization of this idea, discuss itstheoretical properties, and its efficiency.Experimental results with a synthetic 2D tracking problem show that thelattice particle filter is equivalent to a conventional particle filterthat has between 10 and 60% more particles, depending ontheir "sparsity" in the state-space.We also present results on inferring 3D human motion frommoving light displays.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge