Universal Policies for Software-Defined MDPs

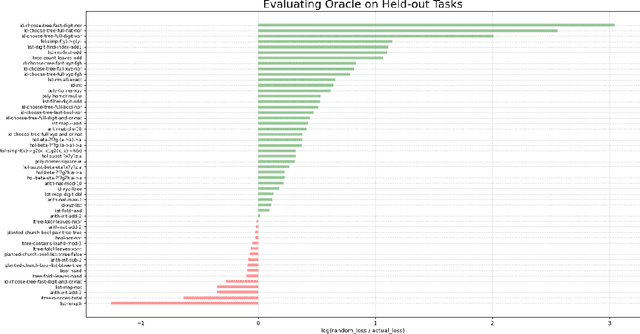
We introduce a new programming paradigm called oracle-guided decision programming in which a program specifies a Markov Decision Process (MDP) and the language provides a universal policy. We prototype a new programming language, Dodona, that manifests this paradigm using a primitive 'choose' representing nondeterministic choice. The Dodona interpreter returns either a value or a choicepoint that includes a lossless encoding of all information necessary in principle to make an optimal decision. Meta-interpreters query Dodona's (neural) oracle on these choicepoints to get policy and value estimates, which they can use to perform heuristic search on the underlying MDP. We demonstrate Dodona's potential for zero-shot heuristic guidance by meta-learning over hundreds of synthetic tasks that simulate basic operations over lists, trees, Church datastructures, polynomials, first-order terms and higher-order terms.

Guiding High-Performance SAT Solvers with Unsat-Core Predictions

The NeuroSAT neural network architecture was recently introduced for predicting properties of propositional formulae. When trained to predict the satisfiability of toy problems, it was shown to find solutions and unsatisfiable cores on its own. However, the authors saw "no obvious path" to using the architecture to improve the state-of-the-art. In this work, we train a simplified NeuroSAT architecture to directly predict the unsatisfiable cores of real problems. We modify several state-of-the-art SAT solvers to periodically replace their variable activity scores with NeuroSAT's prediction of how likely the variables are to appear in an unsatisfiable core. The modified MiniSat solves 10% more problems on SAT-COMP 2018 within the standard 5,000 second timeout than the original does. The modified Glucose solves 11% more problems than the original, while the modified Z3 solves 6% more. The gains are even greater when the training is specialized for a specific distribution of problems; on a benchmark of hard problems from a scheduling domain, the modified Glucose solves 20% more problems than the original does within a one-hour timeout. Our results demonstrate that NeuroSAT can provide effective guidance to high-performance SAT solvers on real problems.

Learning a SAT Solver from Single-Bit Supervision

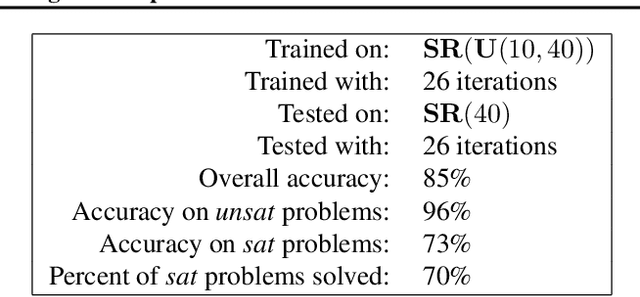
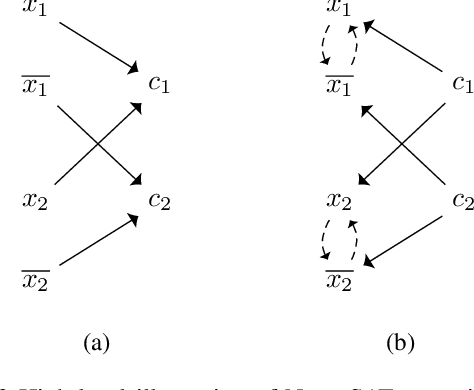
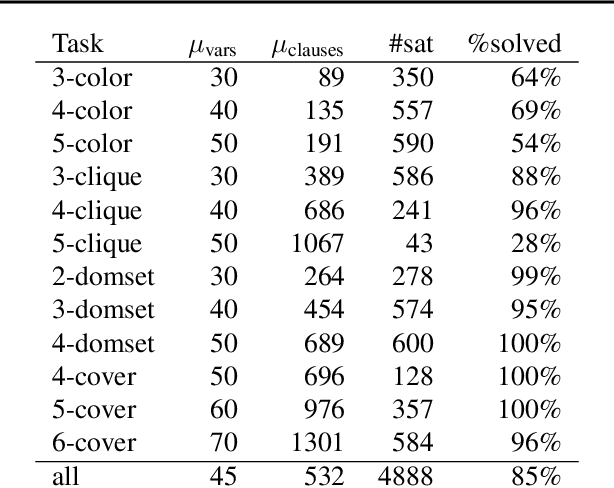
We present NeuroSAT, a message passing neural network that learns to solve SAT problems after only being trained as a classifier to predict satisfiability. Although it is not competitive with state-of-the-art SAT solvers, NeuroSAT can solve problems that are substantially larger and more difficult than it ever saw during training by simply running for more iterations. Moreover, NeuroSAT generalizes to novel distributions; after training only on random SAT problems, at test time it can solve SAT problems encoding graph coloring, clique detection, dominating set, and vertex cover problems, all on a range of distributions over small random graphs.

Developing Bug-Free Machine Learning Systems With Formal Mathematics

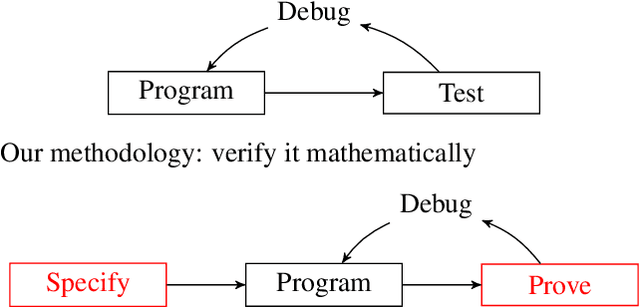
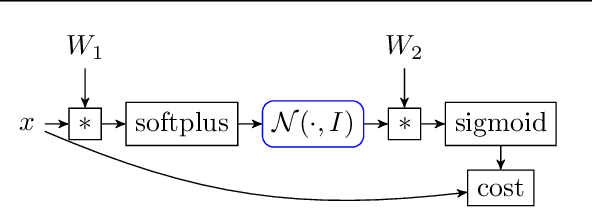
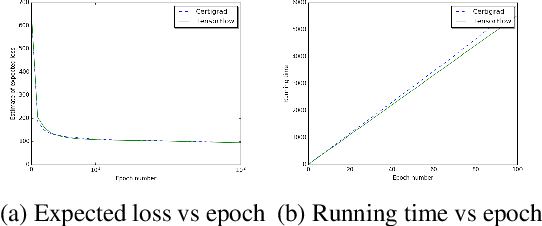
Noisy data, non-convex objectives, model misspecification, and numerical instability can all cause undesired behaviors in machine learning systems. As a result, detecting actual implementation errors can be extremely difficult. We demonstrate a methodology in which developers use an interactive proof assistant to both implement their system and to state a formal theorem defining what it means for their system to be correct. The process of proving this theorem interactively in the proof assistant exposes all implementation errors since any error in the program would cause the proof to fail. As a case study, we implement a new system, Certigrad, for optimizing over stochastic computation graphs, and we generate a formal (i.e. machine-checkable) proof that the gradients sampled by the system are unbiased estimates of the true mathematical gradients. We train a variational autoencoder using Certigrad and find the performance comparable to training the same model in TensorFlow.

Data Programming: Creating Large Training Sets, Quickly

Large labeled training sets are the critical building blocks of supervised learning methods and are key enablers of deep learning techniques. For some applications, creating labeled training sets is the most time-consuming and expensive part of applying machine learning. We therefore propose a paradigm for the programmatic creation of training sets called data programming in which users express weak supervision strategies or domain heuristics as labeling functions, which are programs that label subsets of the data, but that are noisy and may conflict. We show that by explicitly representing this training set labeling process as a generative model, we can "denoise" the generated training set, and establish theoretically that we can recover the parameters of these generative models in a handful of settings. We then show how to modify a discriminative loss function to make it noise-aware, and demonstrate our method over a range of discriminative models including logistic regression and LSTMs. Experimentally, on the 2014 TAC-KBP Slot Filling challenge, we show that data programming would have led to a new winning score, and also show that applying data programming to an LSTM model leads to a TAC-KBP score almost 6 F1 points over a state-of-the-art LSTM baseline (and into second place in the competition). Additionally, in initial user studies we observed that data programming may be an easier way for non-experts to create machine learning models when training data is limited or unavailable.

Venture: a higher-order probabilistic programming platform with programmable inference

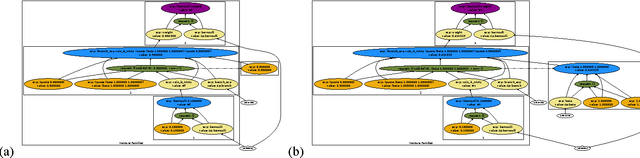
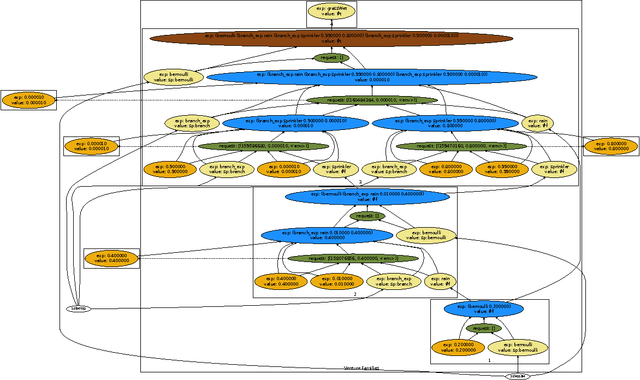
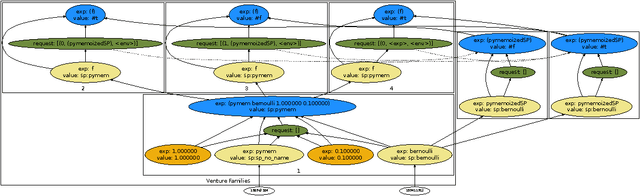
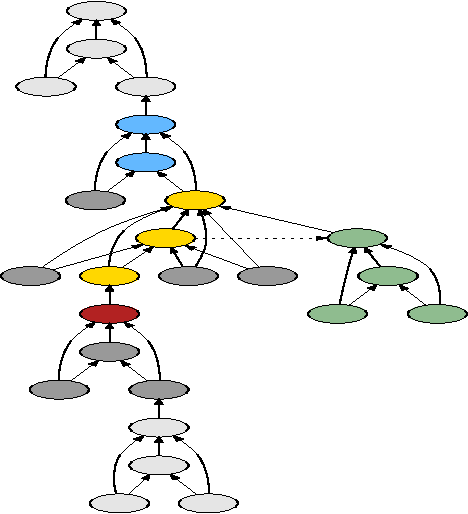
We describe Venture, an interactive virtual machine for probabilistic programming that aims to be sufficiently expressive, extensible, and efficient for general-purpose use. Like Church, probabilistic models and inference problems in Venture are specified via a Turing-complete, higher-order probabilistic language descended from Lisp. Unlike Church, Venture also provides a compositional language for custom inference strategies built out of scalable exact and approximate techniques. We also describe four key aspects of Venture's implementation that build on ideas from probabilistic graphical models. First, we describe the stochastic procedure interface (SPI) that specifies and encapsulates primitive random variables. The SPI supports custom control flow, higher-order probabilistic procedures, partially exchangeable sequences and ``likelihood-free'' stochastic simulators. It also supports external models that do inference over latent variables hidden from Venture. Second, we describe probabilistic execution traces (PETs), which represent execution histories of Venture programs. PETs capture conditional dependencies, existential dependencies and exchangeable coupling. Third, we describe partitions of execution histories called scaffolds that factor global inference problems into coherent sub-problems. Finally, we describe a family of stochastic regeneration algorithms for efficiently modifying PET fragments contained within scaffolds. Stochastic regeneration linear runtime scaling in cases where many previous approaches scaled quadratically. We show how to use stochastic regeneration and the SPI to implement general-purpose inference strategies such as Metropolis-Hastings, Gibbs sampling, and blocked proposals based on particle Markov chain Monte Carlo and mean-field variational inference techniques.