Formal Mathematics Statement Curriculum Learning

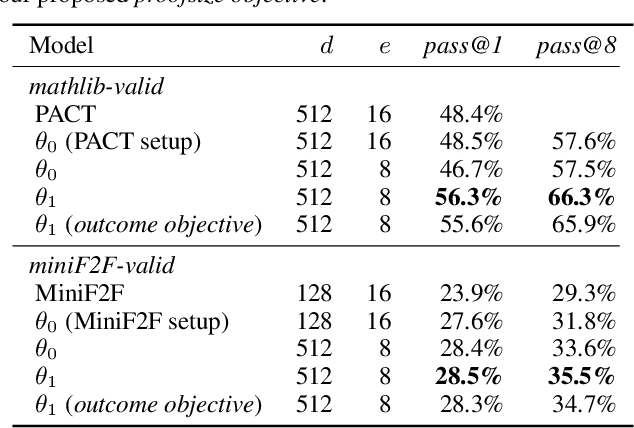
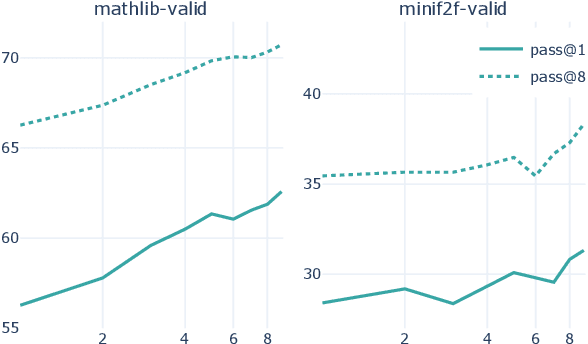
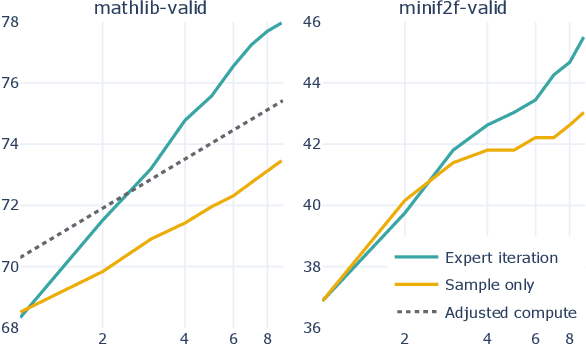
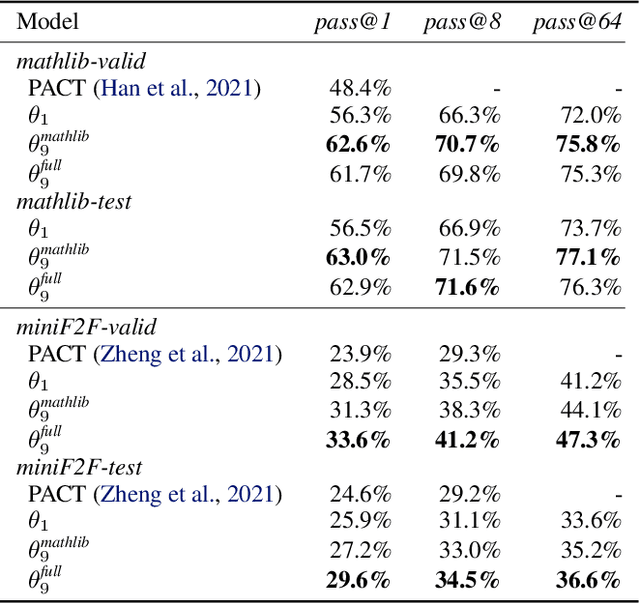
We explore the use of expert iteration in the context of language modeling applied to formal mathematics. We show that at same compute budget, expert iteration, by which we mean proof search interleaved with learning, dramatically outperforms proof search only. We also observe that when applied to a collection of formal statements of sufficiently varied difficulty, expert iteration is capable of finding and solving a curriculum of increasingly difficult problems, without the need for associated ground-truth proofs. Finally, by applying this expert iteration to a manually curated set of problem statements, we achieve state-of-the-art on the miniF2F benchmark, automatically solving multiple challenging problems drawn from high school olympiads.

Text and Code Embeddings by Contrastive Pre-Training

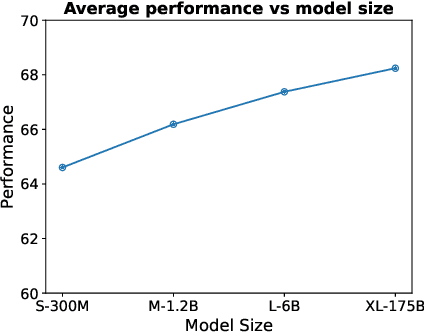
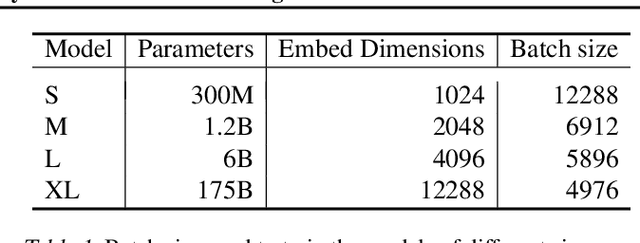
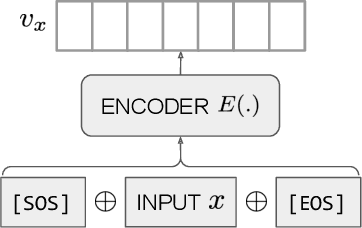
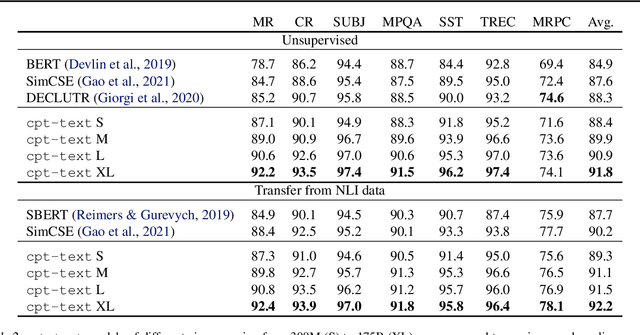
Text embeddings are useful features in many applications such as semantic search and computing text similarity. Previous work typically trains models customized for different use cases, varying in dataset choice, training objective and model architecture. In this work, we show that contrastive pre-training on unsupervised data at scale leads to high quality vector representations of text and code. The same unsupervised text embeddings that achieve new state-of-the-art results in linear-probe classification also display impressive semantic search capabilities and sometimes even perform competitively with fine-tuned models. On linear-probe classification accuracy averaging over 7 tasks, our best unsupervised model achieves a relative improvement of 4% and 1.8% over previous best unsupervised and supervised text embedding models respectively. The same text embeddings when evaluated on large-scale semantic search attains a relative improvement of 23.4%, 14.7%, and 10.6% over previous best unsupervised methods on MSMARCO, Natural Questions and TriviaQA benchmarks, respectively. Similarly to text embeddings, we train code embedding models on (text, code) pairs, obtaining a 20.8% relative improvement over prior best work on code search.

Unsupervised Neural Machine Translation with Generative Language Models Only

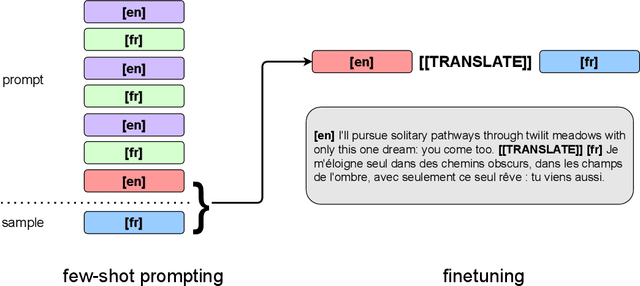
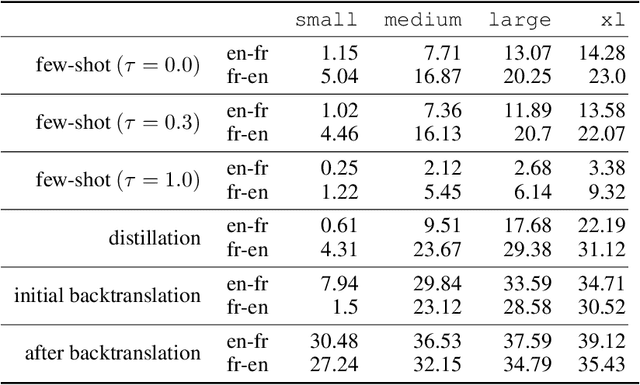
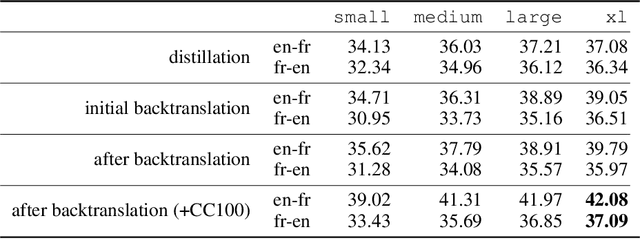
We show how to derive state-of-the-art unsupervised neural machine translation systems from generatively pre-trained language models. Our method consists of three steps: few-shot amplification, distillation, and backtranslation. We first use the zero-shot translation ability of large pre-trained language models to generate translations for a small set of unlabeled sentences. We then amplify these zero-shot translations by using them as few-shot demonstrations for sampling a larger synthetic dataset. This dataset is distilled by discarding the few-shot demonstrations and then fine-tuning. During backtranslation, we repeatedly generate translations for a set of inputs and then fine-tune a single language model on both directions of the translation task at once, ensuring cycle-consistency by swapping the roles of gold monotext and generated translations when fine-tuning. By using our method to leverage GPT-3's zero-shot translation capability, we achieve a new state-of-the-art in unsupervised translation on the WMT14 English-French benchmark, attaining a BLEU score of 42.1.

MiniF2F: a cross-system benchmark for formal Olympiad-level mathematics

We present miniF2F, a dataset of formal Olympiad-level mathematics problems statements intended to provide a unified cross-system benchmark for neural theorem proving. The miniF2F benchmark currently targets Metamath, Lean, and Isabelle and consists of 488 problem statements drawn from the AIME, AMC, and the International Mathematical Olympiad (IMO), as well as material from high-school and undergraduate mathematics courses. We report baseline results using GPT-f, a neural theorem prover based on GPT-3 and provide an analysis of its performance. We intend for miniF2F to be a community-driven effort and hope that our benchmark will help spur advances in neural theorem proving.

Proof Artifact Co-training for Theorem Proving with Language Models

Labeled data for imitation learning of theorem proving in large libraries of formalized mathematics is scarce as such libraries require years of concentrated effort by human specialists to be built. This is particularly challenging when applying large Transformer language models to tactic prediction, because the scaling of performance with respect to model size is quickly disrupted in the data-scarce, easily-overfitted regime. We propose PACT ({\bf P}roof {\bf A}rtifact {\bf C}o-{\bf T}raining), a general methodology for extracting abundant self-supervised data from kernel-level proof terms for co-training alongside the usual tactic prediction objective. We apply this methodology to Lean, an interactive proof assistant which hosts some of the most sophisticated formalized mathematics to date. We instrument Lean with a neural theorem prover driven by a Transformer language model and show that PACT improves theorem proving success rate on a held-out suite of test theorems from 32\% to 48\%.

Universal Policies for Software-Defined MDPs

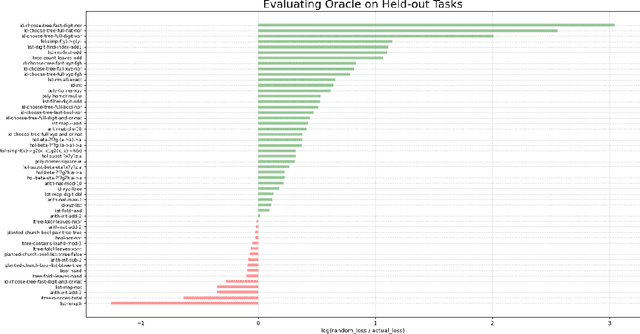
We introduce a new programming paradigm called oracle-guided decision programming in which a program specifies a Markov Decision Process (MDP) and the language provides a universal policy. We prototype a new programming language, Dodona, that manifests this paradigm using a primitive 'choose' representing nondeterministic choice. The Dodona interpreter returns either a value or a choicepoint that includes a lossless encoding of all information necessary in principle to make an optimal decision. Meta-interpreters query Dodona's (neural) oracle on these choicepoints to get policy and value estimates, which they can use to perform heuristic search on the underlying MDP. We demonstrate Dodona's potential for zero-shot heuristic guidance by meta-learning over hundreds of synthetic tasks that simulate basic operations over lists, trees, Church datastructures, polynomials, first-order terms and higher-order terms.

Enhancing SAT solvers with glue variable predictions

Modern SAT solvers routinely operate at scales that make it impractical to query a neural network for every branching decision. NeuroCore, proposed by Selsam and Bjorner, offered a proof-of-concept that neural networks can still accelerate SAT solvers by only periodically refocusing a score-based branching heuristic. However, that work suffered from several limitations: their modified solvers require GPU acceleration, further ablations showed that they were no better than a random baseline on the SATCOMP 2018 benchmark, and their training target of unsat cores required an expensive data pipeline which only labels relatively easy unsatisfiable problems. We address all these limitations, using a simpler network architecture allowing CPU inference for even large industrial problems with millions of clauses, and training instead to predict {\em glue variables}---a target for which it is easier to generate labelled data, and which can also be formulated as a reinforcement learning task. We demonstrate the effectiveness of our approach by modifying the state-of-the-art SAT solver CaDiCaL, improving its performance on SATCOMP 2018 and SATRACE 2019 with supervised learning and its performance on a dataset of SHA-1 preimage attacks with reinforcement learning.