Provably Minimally-Distorted Adversarial Examples

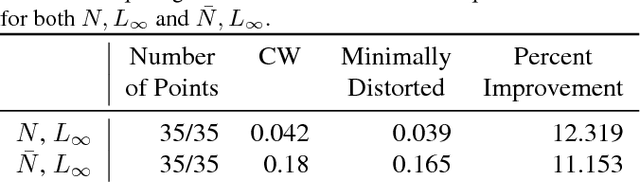
The ability to deploy neural networks in real-world, safety-critical systems is severely limited by the presence of adversarial examples: slightly perturbed inputs that are misclassified by the network. In recent years, several techniques have been proposed for increasing robustness to adversarial examples --- and yet most of these have been quickly shown to be vulnerable to future attacks. For example, over half of the defenses proposed by papers accepted at ICLR 2018 have already been broken. We propose to address this difficulty through formal verification techniques. We show how to construct provably minimally distorted adversarial examples: given an arbitrary neural network and input sample, we can construct adversarial examples which we prove are of minimal distortion. Using this approach, we demonstrate that one of the recent ICLR defense proposals, adversarial retraining, provably succeeds at increasing the distortion required to construct adversarial examples by a factor of 4.2.

Learning a SAT Solver from Single-Bit Supervision

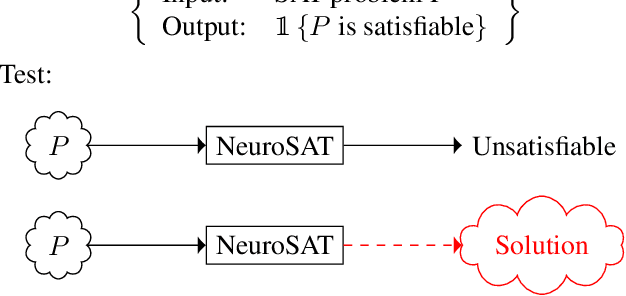
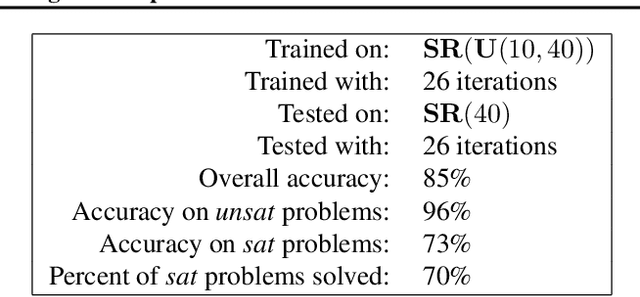
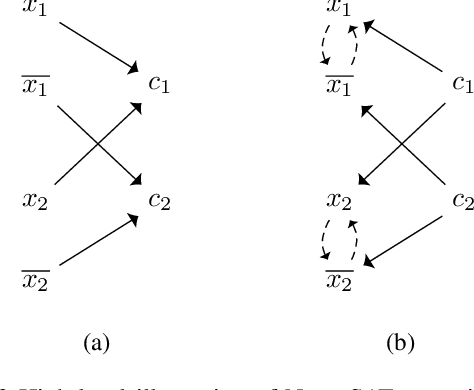
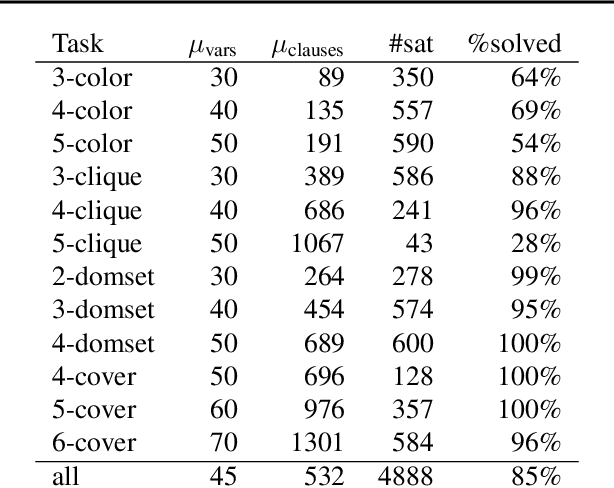
We present NeuroSAT, a message passing neural network that learns to solve SAT problems after only being trained as a classifier to predict satisfiability. Although it is not competitive with state-of-the-art SAT solvers, NeuroSAT can solve problems that are substantially larger and more difficult than it ever saw during training by simply running for more iterations. Moreover, NeuroSAT generalizes to novel distributions; after training only on random SAT problems, at test time it can solve SAT problems encoding graph coloring, clique detection, dominating set, and vertex cover problems, all on a range of distributions over small random graphs.

Towards Proving the Adversarial Robustness of Deep Neural Networks

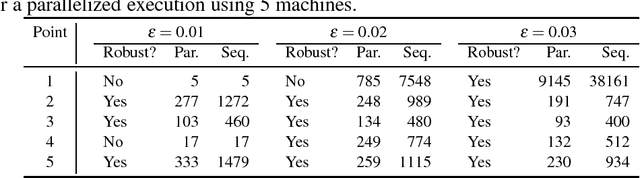
Autonomous vehicles are highly complex systems, required to function reliably in a wide variety of situations. Manually crafting software controllers for these vehicles is difficult, but there has been some success in using deep neural networks generated using machine-learning. However, deep neural networks are opaque to human engineers, rendering their correctness very difficult to prove manually; and existing automated techniques, which were not designed to operate on neural networks, fail to scale to large systems. This paper focuses on proving the adversarial robustness of deep neural networks, i.e. proving that small perturbations to a correctly-classified input to the network cannot cause it to be misclassified. We describe some of our recent and ongoing work on verifying the adversarial robustness of networks, and discuss some of the open questions we have encountered and how they might be addressed.

Developing Bug-Free Machine Learning Systems With Formal Mathematics

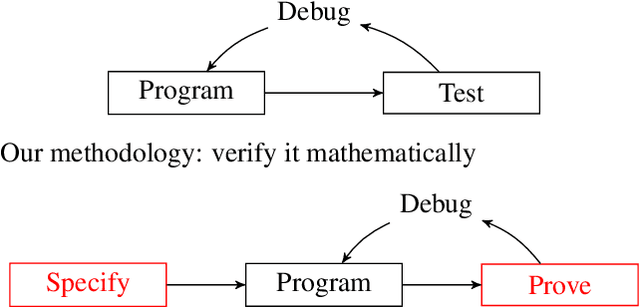
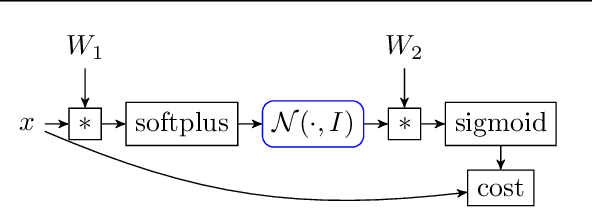
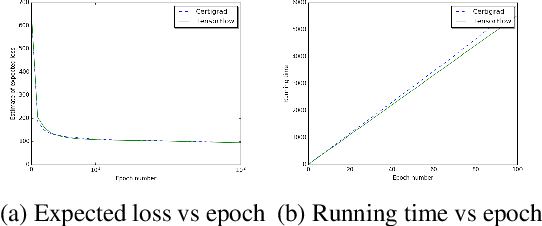
Noisy data, non-convex objectives, model misspecification, and numerical instability can all cause undesired behaviors in machine learning systems. As a result, detecting actual implementation errors can be extremely difficult. We demonstrate a methodology in which developers use an interactive proof assistant to both implement their system and to state a formal theorem defining what it means for their system to be correct. The process of proving this theorem interactively in the proof assistant exposes all implementation errors since any error in the program would cause the proof to fail. As a case study, we implement a new system, Certigrad, for optimizing over stochastic computation graphs, and we generate a formal (i.e. machine-checkable) proof that the gradients sampled by the system are unbiased estimates of the true mathematical gradients. We train a variational autoencoder using Certigrad and find the performance comparable to training the same model in TensorFlow.