Learning a SAT Solver from Single-Bit Supervision

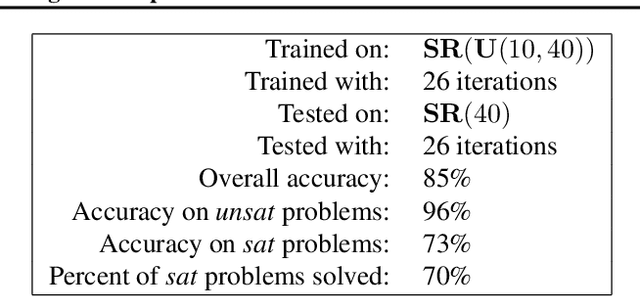
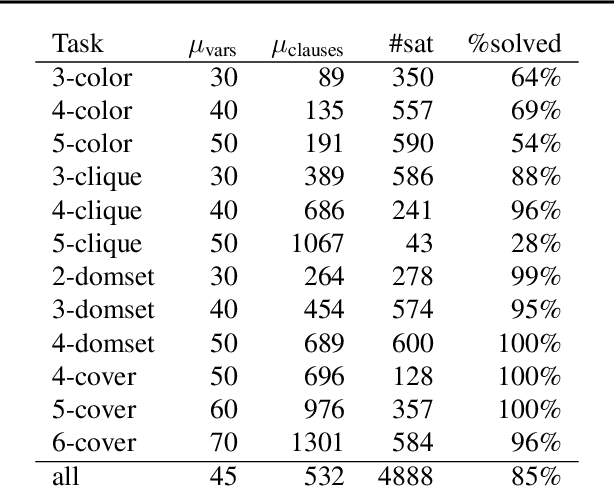
We present NeuroSAT, a message passing neural network that learns to solve SAT problems after only being trained as a classifier to predict satisfiability. Although it is not competitive with state-of-the-art SAT solvers, NeuroSAT can solve problems that are substantially larger and more difficult than it ever saw during training by simply running for more iterations. Moreover, NeuroSAT generalizes to novel distributions; after training only on random SAT problems, at test time it can solve SAT problems encoding graph coloring, clique detection, dominating set, and vertex cover problems, all on a range of distributions over small random graphs.

Graph Neural Networks and Boolean Satisfiability

In this paper we explore whether or not deep neural architectures can learn to classify Boolean satisfiability (SAT). We devote considerable time to discussing the theoretical properties of SAT. Then, we define a graph representation for Boolean formulas in conjunctive normal form, and train neural classifiers over general graph structures called Graph Neural Networks, or GNNs, to recognize features of satisfiability. To the best of our knowledge this has never been tried before. Our preliminary findings are potentially profound. In a weakly-supervised setting, that is, without problem specific feature engineering, Graph Neural Networks can learn features of satisfiability.