From Classical Data to Quantum Advantage -- Quantum Policy Evaluation on Quantum Hardware

Quantum policy evaluation (QPE) is a reinforcement learning (RL) algorithm which is quadratically more efficient than an analogous classical Monte Carlo estimation. It makes use of a direct quantum mechanical realization of a finite Markov decision process, in which the agent and the environment are modeled by unitary operators and exchange states, actions, and rewards in superposition. Previously, the quantum environment has been implemented and parametrized manually for an illustrative benchmark using a quantum simulator. In this paper, we demonstrate how these environment parameters can be learned from a batch of classical observational data through quantum machine learning (QML) on quantum hardware. The learned quantum environment is then applied in QPE to also compute policy evaluations on quantum hardware. Our experiments reveal that, despite challenges such as noise and short coherence times, the integration of QML and QPE shows promising potential for achieving quantum advantage in RL.

Quantum Boltzmann Machines using Parallel Annealing for Medical Image Classification

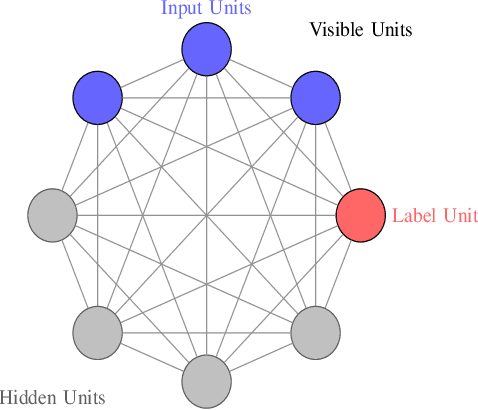
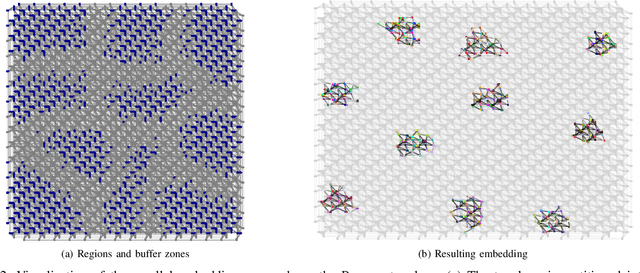
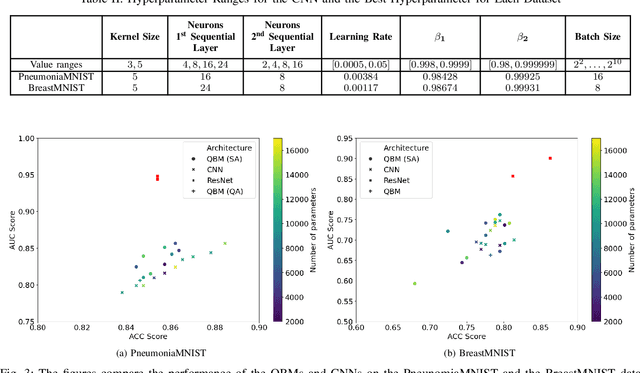
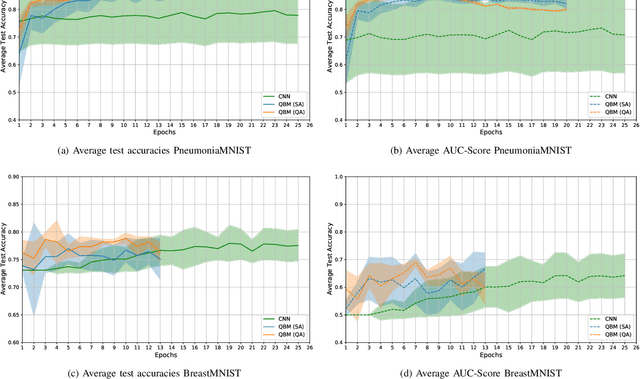
Exploiting the fact that samples drawn from a quantum annealer inherently follow a Boltzmann-like distribution, annealing-based Quantum Boltzmann Machines (QBMs) have gained increasing popularity in the quantum research community. While they harbor great promises for quantum speed-up, their usage currently stays a costly endeavor, as large amounts of QPU time are required to train them. This limits their applicability in the NISQ era. Following the idea of No\`e et al. (2024), who tried to alleviate this cost by incorporating parallel quantum annealing into their unsupervised training of QBMs, this paper presents an improved version of parallel quantum annealing that we employ to train QBMs in a supervised setting. Saving qubits to encode the inputs, the latter setting allows us to test our approach on medical images from the MedMNIST data set (Yang et al., 2023), thereby moving closer to real-world applicability of the technology. Our experiments show that QBMs using our approach already achieve reasonable results, comparable to those of similarly-sized Convolutional Neural Networks (CNNs), with markedly smaller numbers of epochs than these classical models. Our parallel annealing technique leads to a speed-up of almost 70 % compared to regular annealing-based BM executions.

Efficient Quantum One-Class Support Vector Machines for Anomaly Detection Using Randomized Measurements and Variable Subsampling

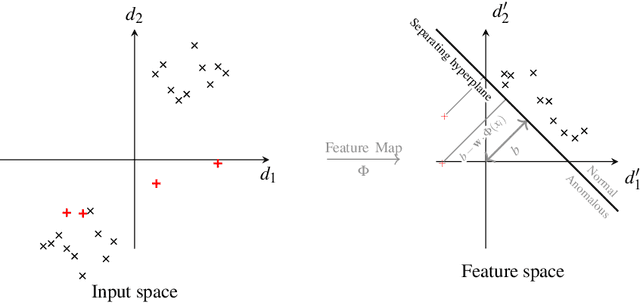
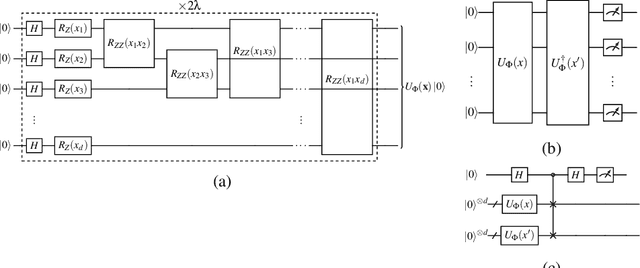
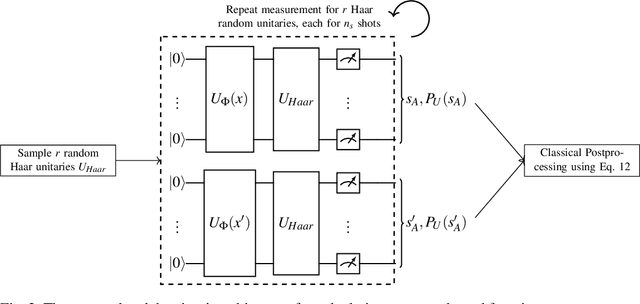
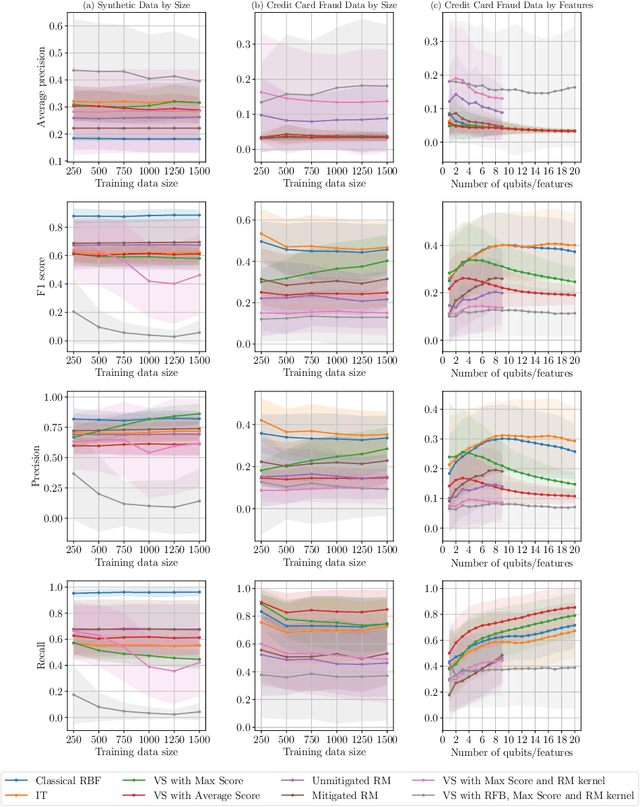
Quantum one-class support vector machines leverage the advantage of quantum kernel methods for semi-supervised anomaly detection. However, their quadratic time complexity with respect to data size poses challenges when dealing with large datasets. In recent work, quantum randomized measurements kernels and variable subsampling were proposed, as two independent methods to address this problem. The former achieves higher average precision, but suffers from variance, while the latter achieves linear complexity to data size and has lower variance. The current work focuses instead on combining these two methods, along with rotated feature bagging, to achieve linear time complexity both to data size and to number of features. Despite their instability, the resulting models exhibit considerably higher performance and faster training and testing times.

Towards Transfer Learning for Large-Scale Image Classification Using Annealing-based Quantum Boltzmann Machines

Quantum Transfer Learning (QTL) recently gained popularity as a hybrid quantum-classical approach for image classification tasks by efficiently combining the feature extraction capabilities of large Convolutional Neural Networks with the potential benefits of Quantum Machine Learning (QML). Existing approaches, however, only utilize gate-based Variational Quantum Circuits for the quantum part of these procedures. In this work we present an approach to employ Quantum Annealing (QA) in QTL-based image classification. Specifically, we propose using annealing-based Quantum Boltzmann Machines as part of a hybrid quantum-classical pipeline to learn the classification of real-world, large-scale data such as medical images through supervised training. We demonstrate our approach by applying it to the three-class COVID-CT-MD dataset, a collection of lung Computed Tomography (CT) scan slices. Using Simulated Annealing as a stand-in for actual QA, we compare our method to classical transfer learning, using a neural network of the same order of magnitude, to display its improved classification performance. We find that our approach consistently outperforms its classical baseline in terms of test accuracy and AUC-ROC-Score and needs less training epochs to do this.

Solving Large Steiner Tree Problems in Graphs for Cost-Efficient Fiber-To-The-Home Network Expansion

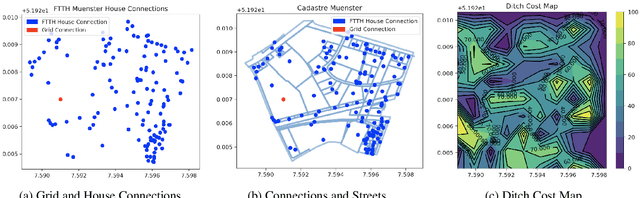
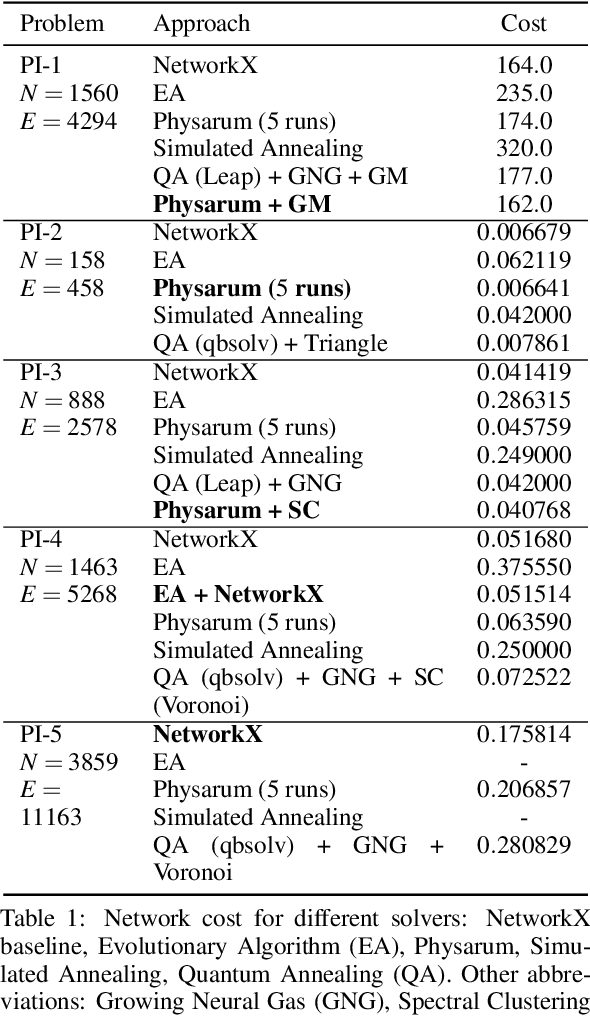
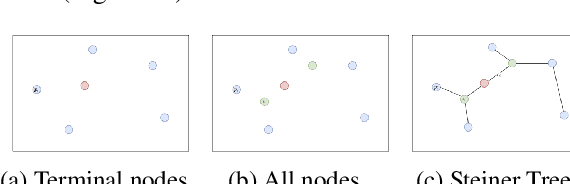
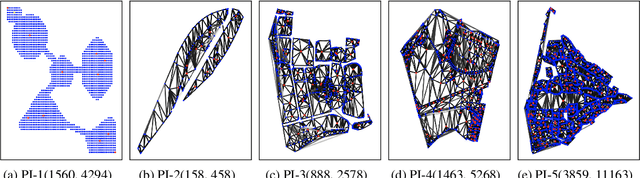
The expansion of Fiber-To-The-Home (FTTH) networks creates high costs due to expensive excavation procedures. Optimizing the planning process and minimizing the cost of the earth excavation work therefore lead to large savings. Mathematically, the FTTH network problem can be described as a minimum Steiner Tree problem. Even though the Steiner Tree problem has already been investigated intensively in the last decades, it might be further optimized with the help of new computing paradigms and emerging approaches. This work studies upcoming technologies, such as Quantum Annealing, Simulated Annealing and nature-inspired methods like Evolutionary Algorithms or slime-mold-based optimization. Additionally, we investigate partitioning and simplifying methods. Evaluated on several real-life problem instances, we could outperform a traditional, widely-used baseline (NetworkX Approximate Solver) on most of the domains. Prior partitioning of the initial graph and the presented slime-mold-based approach were especially valuable for a cost-efficient approximation. Quantum Annealing seems promising, but was limited by the number of available qubits.