Pascal Debus
Quantum Machine Learning Playground
Jul 23, 2025Abstract:This article introduces an innovative interactive visualization tool designed to demystify quantum machine learning (QML) algorithms. Our work is inspired by the success of classical machine learning visualization tools, such as TensorFlow Playground, and aims to bridge the gap in visualization resources specifically for the field of QML. The article includes a comprehensive overview of relevant visualization metaphors from both quantum computing and classical machine learning, the development of an algorithm visualization concept, and the design of a concrete implementation as an interactive web application. By combining common visualization metaphors for the so-called data re-uploading universal quantum classifier as a representative QML model, this article aims to lower the entry barrier to quantum computing and encourage further innovation in the field. The accompanying interactive application is a proposal for the first version of a quantum machine learning playground for learning and exploring QML models.
* Accepted to IEEE Computer Graphics and Applications. Final version: https://doi.org/10.1109/MCG.2024.3456288
Quantum Support Vector Regression for Robust Anomaly Detection
May 02, 2025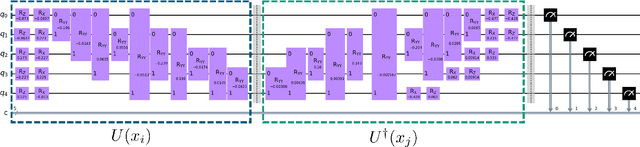
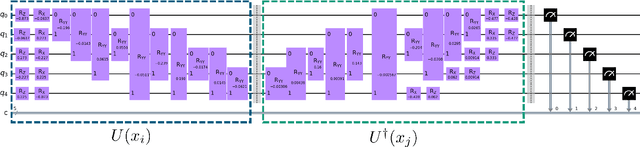
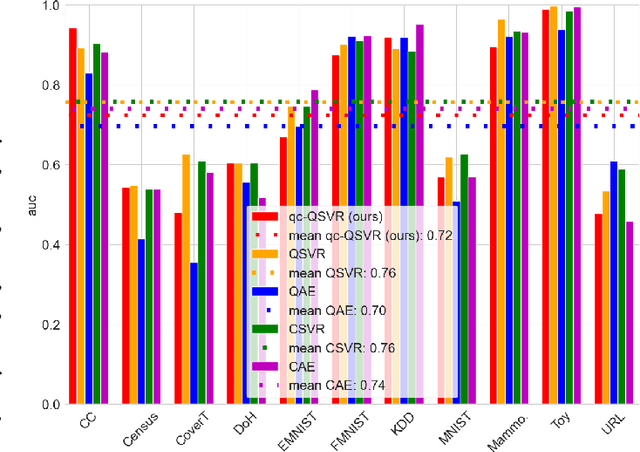
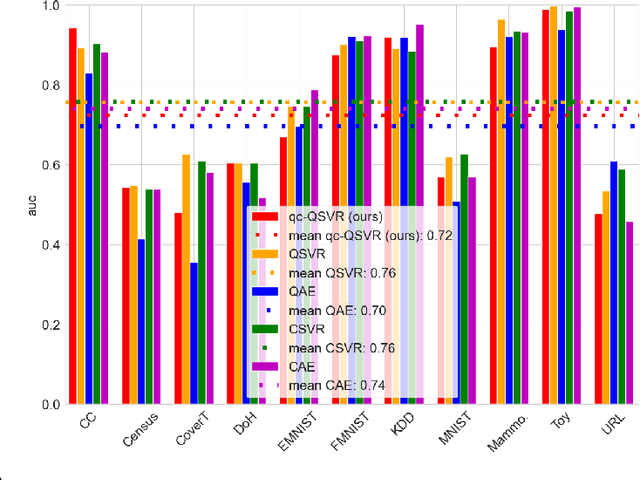
Abstract:Anomaly Detection (AD) is critical in data analysis, particularly within the domain of IT security. In recent years, Machine Learning (ML) algorithms have emerged as a powerful tool for AD in large-scale data. In this study, we explore the potential of quantum ML approaches, specifically quantum kernel methods, for the application to robust AD. We build upon previous work on Quantum Support Vector Regression (QSVR) for semisupervised AD by conducting a comprehensive benchmark on IBM quantum hardware using eleven datasets. Our results demonstrate that QSVR achieves strong classification performance and even outperforms the noiseless simulation on two of these datasets. Moreover, we investigate the influence of - in the NISQ-era inevitable - quantum noise on the performance of the QSVR. Our findings reveal that the model exhibits robustness to depolarizing, phase damping, phase flip, and bit flip noise, while amplitude damping and miscalibration noise prove to be more disruptive. Finally, we explore the domain of Quantum Adversarial Machine Learning and demonstrate that QSVR is highly vulnerable to adversarial attacks and that noise does not improve the adversarial robustness of the model.
Quantum Autoencoder for Multivariate Time Series Anomaly Detection
Apr 24, 2025Abstract:Anomaly Detection (AD) defines the task of identifying observations or events that deviate from typical - or normal - patterns, a critical capability in IT security for recognizing incidents such as system misconfigurations, malware infections, or cyberattacks. In enterprise environments like SAP HANA Cloud systems, this task often involves monitoring high-dimensional, multivariate time series (MTS) derived from telemetry and log data. With the advent of quantum machine learning offering efficient calculations in high-dimensional latent spaces, many avenues open for dealing with such complex data. One approach is the Quantum Autoencoder (QAE), an emerging and promising method with potential for application in both data compression and AD. However, prior applications of QAEs to time series AD have been restricted to univariate data, limiting their relevance for real-world enterprise systems. In this work, we introduce a novel QAE-based framework designed specifically for MTS AD towards enterprise scale. We theoretically develop and experimentally validate the architecture, demonstrating that our QAE achieves performance competitive with neural-network-based autoencoders while requiring fewer trainable parameters. We evaluate our model on datasets that closely reflect SAP system telemetry and show that the proposed QAE is a viable and efficient alternative for semisupervised AD in real-world enterprise settings.
Efficient Quantum One-Class Support Vector Machines for Anomaly Detection Using Randomized Measurements and Variable Subsampling
Jul 30, 2024Abstract:Quantum one-class support vector machines leverage the advantage of quantum kernel methods for semi-supervised anomaly detection. However, their quadratic time complexity with respect to data size poses challenges when dealing with large datasets. In recent work, quantum randomized measurements kernels and variable subsampling were proposed, as two independent methods to address this problem. The former achieves higher average precision, but suffers from variance, while the latter achieves linear complexity to data size and has lower variance. The current work focuses instead on combining these two methods, along with rotated feature bagging, to achieve linear time complexity both to data size and to number of features. Despite their instability, the resulting models exhibit considerably higher performance and faster training and testing times.
QUACK: Quantum Aligned Centroid Kernel
May 01, 2024Abstract:Quantum computing (QC) seems to show potential for application in machine learning (ML). In particular quantum kernel methods (QKM) exhibit promising properties for use in supervised ML tasks. However, a major disadvantage of kernel methods is their unfavorable quadratic scaling with the number of training samples. Together with the limits imposed by currently available quantum hardware (NISQ devices) with their low qubit coherence times, small number of qubits, and high error rates, the use of QC in ML at an industrially relevant scale is currently impossible. As a small step in improving the potential applications of QKMs, we introduce QUACK, a quantum kernel algorithm whose time complexity scales linear with the number of samples during training, and independent of the number of training samples in the inference stage. In the training process, only the kernel entries for the samples and the centers of the classes are calculated, i.e. the maximum shape of the kernel for n samples and c classes is (n, c). During training, the parameters of the quantum kernel and the positions of the centroids are optimized iteratively. In the inference stage, for every new sample the circuit is only evaluated for every centroid, i.e. c times. We show that the QUACK algorithm nevertheless provides satisfactory results and can perform at a similar level as classical kernel methods with quadratic scaling during training. In addition, our (simulated) algorithm is able to handle high-dimensional datasets such as MNIST with 784 features without any dimensionality reduction.
A Comparative Analysis of Adversarial Robustness for Quantum and Classical Machine Learning Models
Apr 24, 2024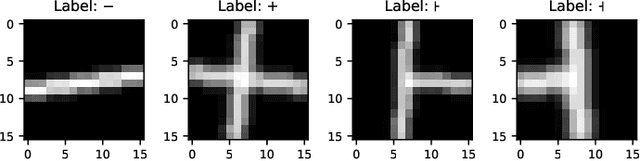
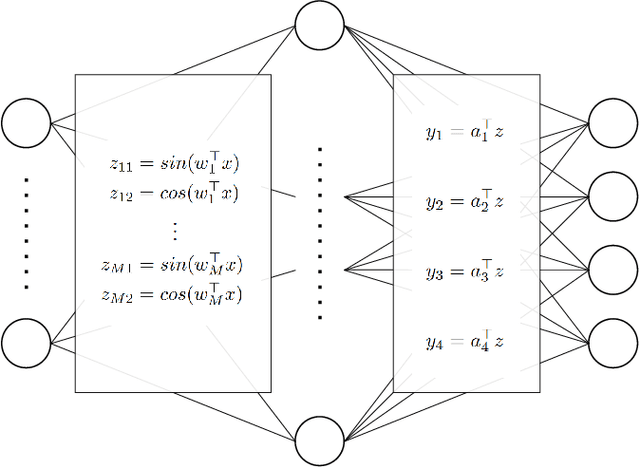
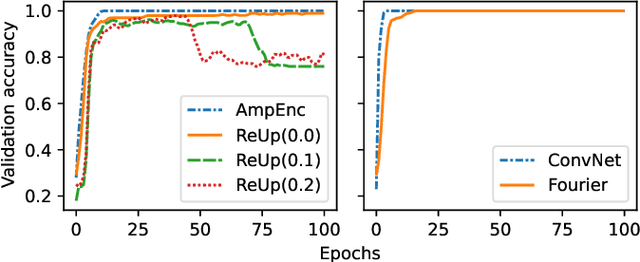
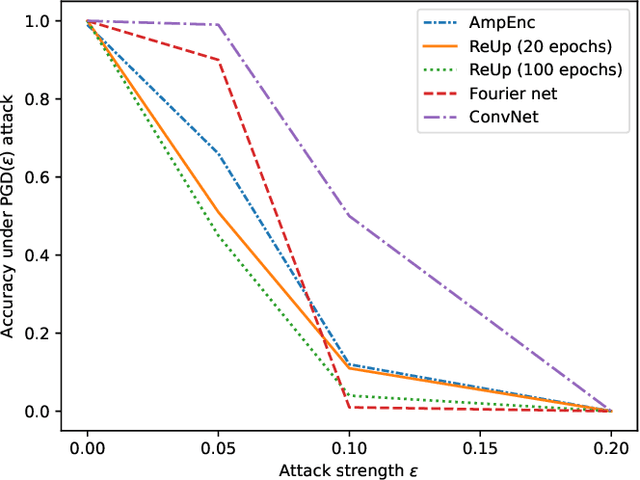
Abstract:Quantum machine learning (QML) continues to be an area of tremendous interest from research and industry. While QML models have been shown to be vulnerable to adversarial attacks much in the same manner as classical machine learning models, it is still largely unknown how to compare adversarial attacks on quantum versus classical models. In this paper, we show how to systematically investigate the similarities and differences in adversarial robustness of classical and quantum models using transfer attacks, perturbation patterns and Lipschitz bounds. More specifically, we focus on classification tasks on a handcrafted dataset that allows quantitative analysis for feature attribution. This enables us to get insight, both theoretically and experimentally, on the robustness of classification networks. We start by comparing typical QML model architectures such as amplitude and re-upload encoding circuits with variational parameters to a classical ConvNet architecture. Next, we introduce a classical approximation of QML circuits (originally obtained with Random Fourier Features sampling but adapted in this work to fit a trainable encoding) and evaluate this model, denoted Fourier network, in comparison to other architectures. Our findings show that this Fourier network can be seen as a "middle ground" on the quantum-classical boundary. While adversarial attacks successfully transfer across this boundary in both directions, we also show that regularization helps quantum networks to be more robust, which has direct impact on Lipschitz bounds and transfer attacks.
Towards Efficient Quantum Anomaly Detection: One-Class SVMs using Variable Subsampling and Randomized Measurements
Dec 14, 2023



Abstract:Quantum computing, with its potential to enhance various machine learning tasks, allows significant advancements in kernel calculation and model precision. Utilizing the one-class Support Vector Machine alongside a quantum kernel, known for its classically challenging representational capacity, notable improvements in average precision compared to classical counterparts were observed in previous studies. Conventional calculations of these kernels, however, present a quadratic time complexity concerning data size, posing challenges in practical applications. To mitigate this, we explore two distinct approaches: utilizing randomized measurements to evaluate the quantum kernel and implementing the variable subsampling ensemble method, both targeting linear time complexity. Experimental results demonstrate a substantial reduction in training and inference times by up to 95\% and 25\% respectively, employing these methods. Although unstable, the average precision of randomized measurements discernibly surpasses that of the classical Radial Basis Function kernel, suggesting a promising direction for further research in scalable, efficient quantum computing applications in machine learning.
Protecting Publicly Available Data With Machine Learning Shortcuts
Oct 30, 2023Abstract:Machine-learning (ML) shortcuts or spurious correlations are artifacts in datasets that lead to very good training and test performance but severely limit the model's generalization capability. Such shortcuts are insidious because they go unnoticed due to good in-domain test performance. In this paper, we explore the influence of different shortcuts and show that even simple shortcuts are difficult to detect by explainable AI methods. We then exploit this fact and design an approach to defend online databases against crawlers: providers such as dating platforms, clothing manufacturers, or used car dealers have to deal with a professionalized crawling industry that grabs and resells data points on a large scale. We show that a deterrent can be created by deliberately adding ML shortcuts. Such augmented datasets are then unusable for ML use cases, which deters crawlers and the unauthorized use of data from the internet. Using real-world data from three use cases, we show that the proposed approach renders such collected data unusable, while the shortcut is at the same time difficult to notice in human perception. Thus, our proposed approach can serve as a proactive protection against illegitimate data crawling.
Semisupervised Anomaly Detection using Support Vector Regression with Quantum Kernel
Aug 01, 2023



Abstract:Anomaly detection (AD) involves identifying observations or events that deviate in some way from the rest of the data. Machine learning techniques have shown success in automating this process by detecting hidden patterns and deviations in large-scale data. The potential of quantum computing for machine learning has been widely recognized, leading to extensive research efforts to develop suitable quantum machine learning (QML) algorithms. In particular, the search for QML algorithms for near-term NISQ devices is in full swing. However, NISQ devices pose additional challenges due to their limited qubit coherence times, low number of qubits, and high error rates. Kernel methods based on quantum kernel estimation have emerged as a promising approach to QML on NISQ devices, offering theoretical guarantees, versatility, and compatibility with NISQ constraints. Especially support vector machines (SVM) utilizing quantum kernel estimation have shown success in various supervised learning tasks. However, in the context of AD, semisupervised learning is of great relevance, and yet there is limited research published in this area. This paper introduces an approach to semisupervised AD based on the reconstruction loss of a support vector regression (SVR) with quantum kernel. This novel model is an alternative to the variational quantum and quantum kernel one-class classifiers, and is compared to a quantum autoencoder as quantum baseline and a SVR with radial-basis-function (RBF) kernel as well as a classical autoencoder as classical baselines. The models are benchmarked extensively on 10 real-world AD data sets and one toy data set, and it is shown that our SVR model with quantum kernel performs better than the SVR with RBF kernel as well as all other models, achieving highest mean AUC over all data sets. In addition, our QSVR outperforms the quantum autoencoder on 9 out of 11 data sets.
Deep Reinforcement Learning for Backup Strategies against Adversaries
Feb 12, 2021
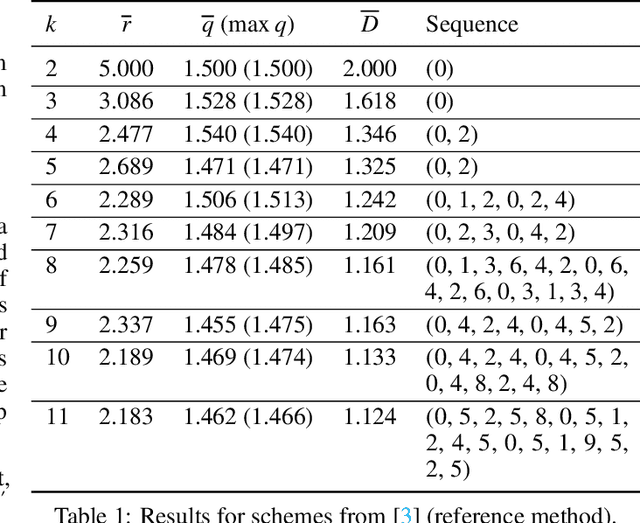

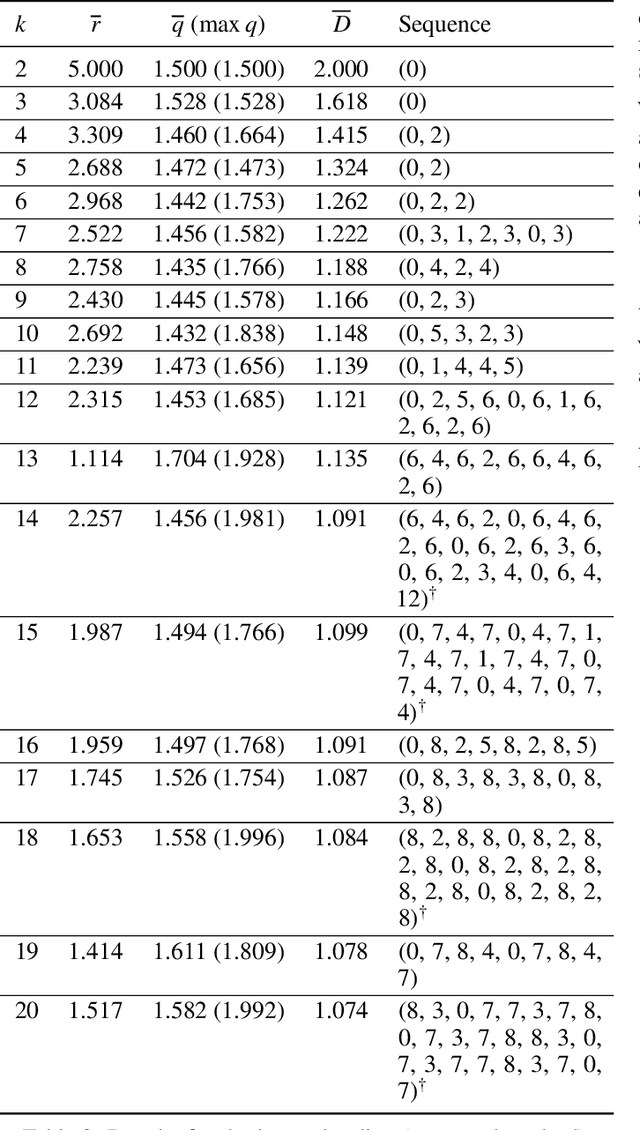
Abstract:Many defensive measures in cyber security are still dominated by heuristics, catalogs of standard procedures, and best practices. Considering the case of data backup strategies, we aim towards mathematically modeling the underlying threat models and decision problems. By formulating backup strategies in the language of stochastic processes, we can translate the challenge of finding optimal defenses into a reinforcement learning problem. This enables us to train autonomous agents that learn to optimally support planning of defense processes. In particular, we tackle the problem of finding an optimal backup scheme in the following adversarial setting: Given $k$ backup devices, the goal is to defend against an attacker who can infect data at one time but chooses to destroy or encrypt it at a later time, potentially also corrupting multiple backups made in between. In this setting, the usual round-robin scheme, which always replaces the oldest backup, is no longer optimal with respect to avoidable exposure. Thus, to find a defense strategy, we model the problem as a hybrid discrete-continuous action space Markov decision process and subsequently solve it using deep deterministic policy gradients. We show that the proposed algorithm can find storage device update schemes which match or exceed existing schemes with respect to various exposure metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge