Sebastian Issel
Quantum Machine Learning Playground
Jul 23, 2025Abstract:This article introduces an innovative interactive visualization tool designed to demystify quantum machine learning (QML) algorithms. Our work is inspired by the success of classical machine learning visualization tools, such as TensorFlow Playground, and aims to bridge the gap in visualization resources specifically for the field of QML. The article includes a comprehensive overview of relevant visualization metaphors from both quantum computing and classical machine learning, the development of an algorithm visualization concept, and the design of a concrete implementation as an interactive web application. By combining common visualization metaphors for the so-called data re-uploading universal quantum classifier as a representative QML model, this article aims to lower the entry barrier to quantum computing and encourage further innovation in the field. The accompanying interactive application is a proposal for the first version of a quantum machine learning playground for learning and exploring QML models.
* Accepted to IEEE Computer Graphics and Applications. Final version: https://doi.org/10.1109/MCG.2024.3456288
Quantum Support Vector Regression for Robust Anomaly Detection
May 02, 2025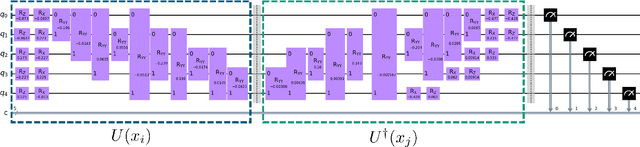
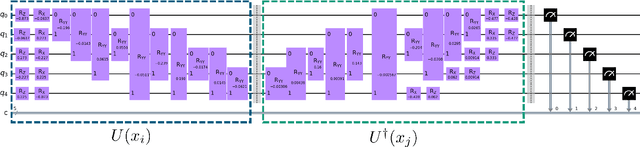
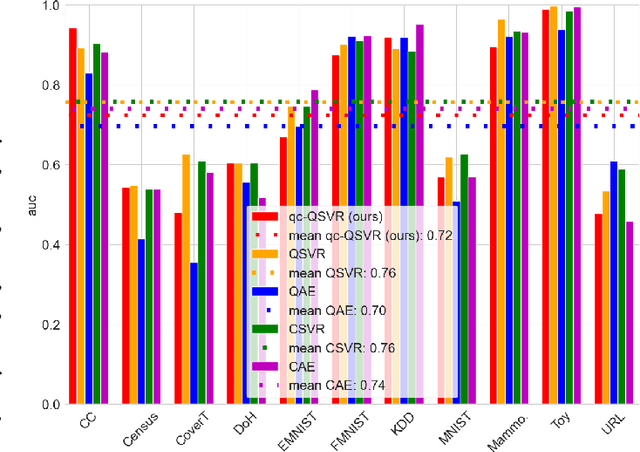
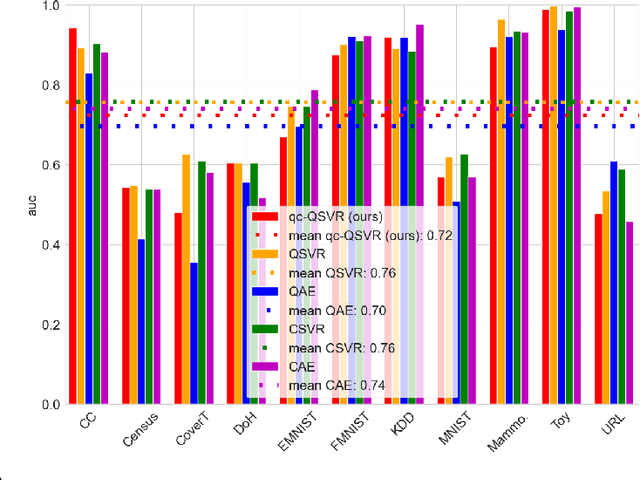
Abstract:Anomaly Detection (AD) is critical in data analysis, particularly within the domain of IT security. In recent years, Machine Learning (ML) algorithms have emerged as a powerful tool for AD in large-scale data. In this study, we explore the potential of quantum ML approaches, specifically quantum kernel methods, for the application to robust AD. We build upon previous work on Quantum Support Vector Regression (QSVR) for semisupervised AD by conducting a comprehensive benchmark on IBM quantum hardware using eleven datasets. Our results demonstrate that QSVR achieves strong classification performance and even outperforms the noiseless simulation on two of these datasets. Moreover, we investigate the influence of - in the NISQ-era inevitable - quantum noise on the performance of the QSVR. Our findings reveal that the model exhibits robustness to depolarizing, phase damping, phase flip, and bit flip noise, while amplitude damping and miscalibration noise prove to be more disruptive. Finally, we explore the domain of Quantum Adversarial Machine Learning and demonstrate that QSVR is highly vulnerable to adversarial attacks and that noise does not improve the adversarial robustness of the model.
QUACK: Quantum Aligned Centroid Kernel
May 01, 2024Abstract:Quantum computing (QC) seems to show potential for application in machine learning (ML). In particular quantum kernel methods (QKM) exhibit promising properties for use in supervised ML tasks. However, a major disadvantage of kernel methods is their unfavorable quadratic scaling with the number of training samples. Together with the limits imposed by currently available quantum hardware (NISQ devices) with their low qubit coherence times, small number of qubits, and high error rates, the use of QC in ML at an industrially relevant scale is currently impossible. As a small step in improving the potential applications of QKMs, we introduce QUACK, a quantum kernel algorithm whose time complexity scales linear with the number of samples during training, and independent of the number of training samples in the inference stage. In the training process, only the kernel entries for the samples and the centers of the classes are calculated, i.e. the maximum shape of the kernel for n samples and c classes is (n, c). During training, the parameters of the quantum kernel and the positions of the centroids are optimized iteratively. In the inference stage, for every new sample the circuit is only evaluated for every centroid, i.e. c times. We show that the QUACK algorithm nevertheless provides satisfactory results and can perform at a similar level as classical kernel methods with quadratic scaling during training. In addition, our (simulated) algorithm is able to handle high-dimensional datasets such as MNIST with 784 features without any dimensionality reduction.
Semisupervised Anomaly Detection using Support Vector Regression with Quantum Kernel
Aug 01, 2023



Abstract:Anomaly detection (AD) involves identifying observations or events that deviate in some way from the rest of the data. Machine learning techniques have shown success in automating this process by detecting hidden patterns and deviations in large-scale data. The potential of quantum computing for machine learning has been widely recognized, leading to extensive research efforts to develop suitable quantum machine learning (QML) algorithms. In particular, the search for QML algorithms for near-term NISQ devices is in full swing. However, NISQ devices pose additional challenges due to their limited qubit coherence times, low number of qubits, and high error rates. Kernel methods based on quantum kernel estimation have emerged as a promising approach to QML on NISQ devices, offering theoretical guarantees, versatility, and compatibility with NISQ constraints. Especially support vector machines (SVM) utilizing quantum kernel estimation have shown success in various supervised learning tasks. However, in the context of AD, semisupervised learning is of great relevance, and yet there is limited research published in this area. This paper introduces an approach to semisupervised AD based on the reconstruction loss of a support vector regression (SVR) with quantum kernel. This novel model is an alternative to the variational quantum and quantum kernel one-class classifiers, and is compared to a quantum autoencoder as quantum baseline and a SVR with radial-basis-function (RBF) kernel as well as a classical autoencoder as classical baselines. The models are benchmarked extensively on 10 real-world AD data sets and one toy data set, and it is shown that our SVR model with quantum kernel performs better than the SVR with RBF kernel as well as all other models, achieving highest mean AUC over all data sets. In addition, our QSVR outperforms the quantum autoencoder on 9 out of 11 data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge