Efficient Quantum One-Class Support Vector Machines for Anomaly Detection Using Randomized Measurements and Variable Subsampling

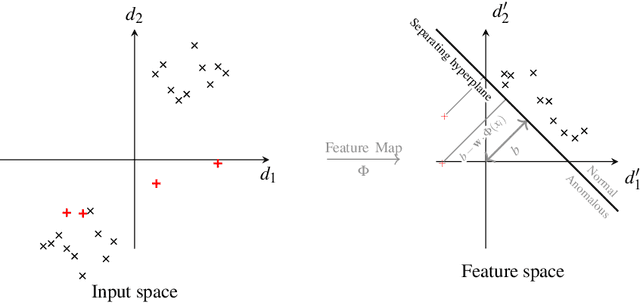
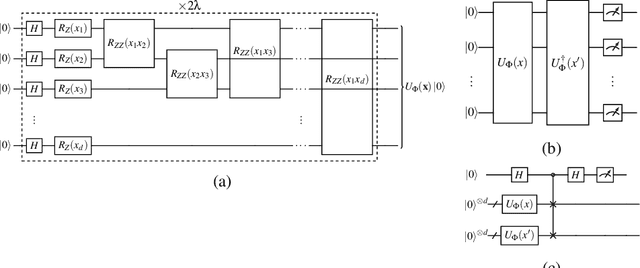
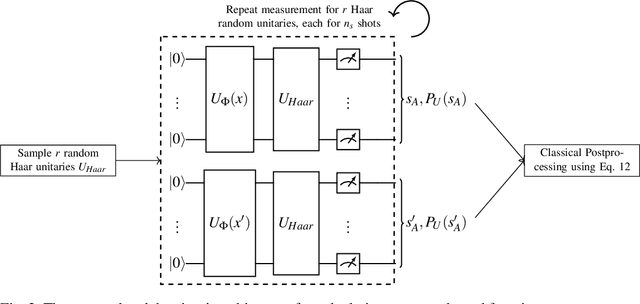
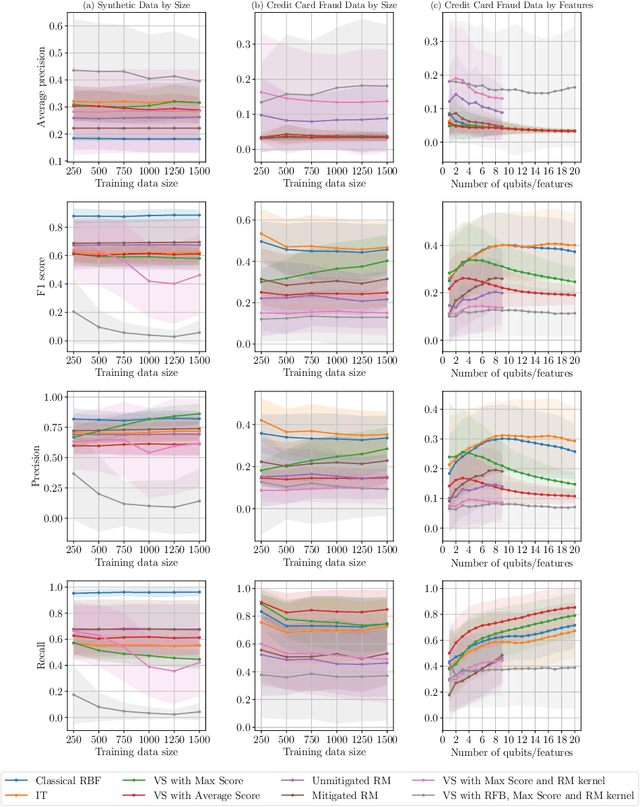
Quantum one-class support vector machines leverage the advantage of quantum kernel methods for semi-supervised anomaly detection. However, their quadratic time complexity with respect to data size poses challenges when dealing with large datasets. In recent work, quantum randomized measurements kernels and variable subsampling were proposed, as two independent methods to address this problem. The former achieves higher average precision, but suffers from variance, while the latter achieves linear complexity to data size and has lower variance. The current work focuses instead on combining these two methods, along with rotated feature bagging, to achieve linear time complexity both to data size and to number of features. Despite their instability, the resulting models exhibit considerably higher performance and faster training and testing times.

Towards Efficient Quantum Anomaly Detection: One-Class SVMs using Variable Subsampling and Randomized Measurements

Quantum computing, with its potential to enhance various machine learning tasks, allows significant advancements in kernel calculation and model precision. Utilizing the one-class Support Vector Machine alongside a quantum kernel, known for its classically challenging representational capacity, notable improvements in average precision compared to classical counterparts were observed in previous studies. Conventional calculations of these kernels, however, present a quadratic time complexity concerning data size, posing challenges in practical applications. To mitigate this, we explore two distinct approaches: utilizing randomized measurements to evaluate the quantum kernel and implementing the variable subsampling ensemble method, both targeting linear time complexity. Experimental results demonstrate a substantial reduction in training and inference times by up to 95\% and 25\% respectively, employing these methods. Although unstable, the average precision of randomized measurements discernibly surpasses that of the classical Radial Basis Function kernel, suggesting a promising direction for further research in scalable, efficient quantum computing applications in machine learning.