Tobias Rohe
Quantum King-Ring Domination in Chess: A QAOA Approach
Jan 01, 2026Abstract:The Quantum Approximate Optimization Algorithm (QAOA) is extensively benchmarked on synthetic random instances such as MaxCut, TSP, and SAT problems, but these lack semantic structure and human interpretability, offering limited insight into performance on real-world problems with meaningful constraints. We introduce Quantum King-Ring Domination (QKRD), a NISQ-scale benchmark derived from chess tactical positions that provides 5,000 structured instances with one-hot constraints, spatial locality, and 10--40 qubit scale. The benchmark pairs human-interpretable coverage metrics with intrinsic validation against classical heuristics, enabling algorithmic conclusions without external oracles. Using QKRD, we systematically evaluate QAOA design choices and find that constraint-preserving mixers (XY, domain-wall) converge approximately 13 steps faster than standard mixers (p<10^{-7}, d\approx0.5) while eliminating penalty tuning, warm-start strategies reduce convergence by 45 steps (p<10^{-127}, d=3.35) with energy improvements exceeding d=8, and Conditional Value-at-Risk (CVaR) optimization yields an informative negative result with worse energy (p<10^{-40}, d=1.21) and no coverage benefit. Intrinsic validation shows QAOA outperforms greedy heuristics by 12.6\% and random selection by 80.1\%. Our results demonstrate that structured benchmarks reveal advantages of problem-informed QAOA techniques obscured in random instances. We release all code, data, and experimental artifacts for reproducible NISQ algorithm research.
Topology-Guided Quantum GANs for Constrained Graph Generation
Dec 11, 2025Abstract:Quantum computing (QC) promises theoretical advantages, benefiting computational problems that would not be efficiently classically simulatable. However, much of this theoretical speedup depends on the quantum circuit design solving the problem. We argue that QC literature has yet to explore more domain specific ansatz-topologies, instead of relying on generic, one-size-fits-all architectures. In this work, we show that incorporating task-specific inductive biases -- specifically geometric priors -- into quantum circuit design can enhance the performance of hybrid Quantum Generative Adversarial Networks (QuGANs) on the task of generating geometrically constrained K4 graphs. We evaluate a portfolio of entanglement topologies and loss-function designs to assess their impact on both statistical fidelity and compliance with geometric constraints, including the Triangle and Ptolemaic inequalities. Our results show that aligning circuit topology with the underlying problem structure yields substantial benefits: the Triangle-topology QuGAN achieves the highest geometric validity among quantum models and matches the performance of classical Generative Adversarial Networks (GAN). Additionally, we showcase how specific architectural choices, such as entangling gate types, variance regularization and output-scaling govern the trade-off between geometric consistency and distributional accuracy, thus emphasizing the value of structured, task-aware quantum ansatz-topologies.
Quantum Boltzmann Machines using Parallel Annealing for Medical Image Classification
Jul 18, 2025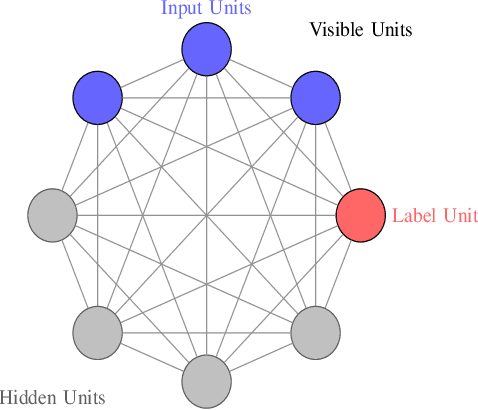
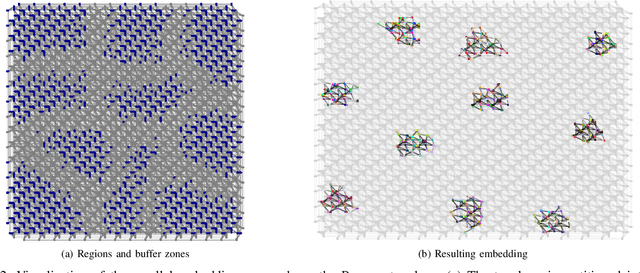
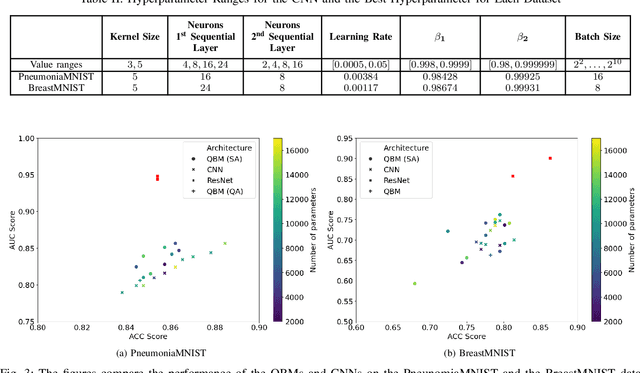
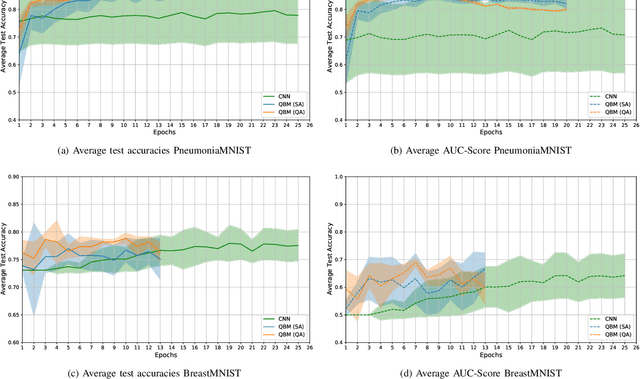
Abstract:Exploiting the fact that samples drawn from a quantum annealer inherently follow a Boltzmann-like distribution, annealing-based Quantum Boltzmann Machines (QBMs) have gained increasing popularity in the quantum research community. While they harbor great promises for quantum speed-up, their usage currently stays a costly endeavor, as large amounts of QPU time are required to train them. This limits their applicability in the NISQ era. Following the idea of No\`e et al. (2024), who tried to alleviate this cost by incorporating parallel quantum annealing into their unsupervised training of QBMs, this paper presents an improved version of parallel quantum annealing that we employ to train QBMs in a supervised setting. Saving qubits to encode the inputs, the latter setting allows us to test our approach on medical images from the MedMNIST data set (Yang et al., 2023), thereby moving closer to real-world applicability of the technology. Our experiments show that QBMs using our approach already achieve reasonable results, comparable to those of similarly-sized Convolutional Neural Networks (CNNs), with markedly smaller numbers of epochs than these classical models. Our parallel annealing technique leads to a speed-up of almost 70 % compared to regular annealing-based BM executions.
Investigating Parameter-Efficiency of Hybrid QuGANs Based on Geometric Properties of Generated Sea Route Graphs
Jan 15, 2025Abstract:The demand for artificially generated data for the development, training and testing of new algorithms is omnipresent. Quantum computing (QC), does offer the hope that its inherent probabilistic functionality can be utilised in this field of generative artificial intelligence. In this study, we use quantum-classical hybrid generative adversarial networks (QuGANs) to artificially generate graphs of shipping routes. We create a training dataset based on real shipping data and investigate to what extent QuGANs are able to learn and reproduce inherent distributions and geometric features of this data. We compare hybrid QuGANs with classical Generative Adversarial Networks (GANs), with a special focus on their parameter efficiency. Our results indicate that QuGANs are indeed able to quickly learn and represent underlying geometric properties and distributions, although they seem to have difficulties in introducing variance into the sampled data. Compared to classical GANs of greater size, measured in the number of parameters used, some QuGANs show similar result quality. Our reference to concrete use cases, such as the generation of shipping data, provides an illustrative example and demonstrate the potential and diversity in which QC can be used.
Optimization of Link Configuration for Satellite Communication Using Reinforcement Learning
Jan 14, 2025Abstract:Satellite communication is a key technology in our modern connected world. With increasingly complex hardware, one challenge is to efficiently configure links (connections) on a satellite transponder. Planning an optimal link configuration is extremely complex and depends on many parameters and metrics. The optimal use of the limited resources, bandwidth and power of the transponder is crucial. Such an optimization problem can be approximated using metaheuristic methods such as simulated annealing, but recent research results also show that reinforcement learning can achieve comparable or even better performance in optimization methods. However, there have not yet been any studies on link configuration on satellite transponders. In order to close this research gap, a transponder environment was developed as part of this work. For this environment, the performance of the reinforcement learning algorithm PPO was compared with the metaheuristic simulated annealing in two experiments. The results show that Simulated Annealing delivers better results for this static problem than the PPO algorithm, however, the research in turn also underlines the potential of reinforcement learning for optimization problems.
Coconut Palm Tree Counting on Drone Images with Deep Object Detection and Synthetic Training Data
Dec 16, 2024



Abstract:Drones have revolutionized various domains, including agriculture. Recent advances in deep learning have propelled among other things object detection in computer vision. This study utilized YOLO, a real-time object detector, to identify and count coconut palm trees in Ghanaian farm drone footage. The farm presented has lost track of its trees due to different planting phases. While manual counting would be very tedious and error-prone, accurately determining the number of trees is crucial for efficient planning and management of agricultural processes, especially for optimizing yields and predicting production. We assessed YOLO for palm detection within a semi-automated framework, evaluated accuracy augmentations, and pondered its potential for farmers. Data was captured in September 2022 via drones. To optimize YOLO with scarce data, synthetic images were created for model training and validation. The YOLOv7 model, pretrained on the COCO dataset (excluding coconut palms), was adapted using tailored data. Trees from footage were repositioned on synthetic images, with testing on distinct authentic images. In our experiments, we adjusted hyperparameters, improving YOLO's mean average precision (mAP). We also tested various altitudes to determine the best drone height. From an initial mAP@.5 of $0.65$, we achieved 0.88, highlighting the value of synthetic images in agricultural scenarios.
A Study on Optimization Techniques for Variational Quantum Circuits in Reinforcement Learning
May 20, 2024Abstract:Quantum Computing aims to streamline machine learning, making it more effective with fewer trainable parameters. This reduction of parameters can speed up the learning process and reduce the use of computational resources. However, in the current phase of quantum computing development, known as the noisy intermediate-scale quantum era (NISQ), learning is difficult due to a limited number of qubits and widespread quantum noise. To overcome these challenges, researchers are focusing on variational quantum circuits (VQCs). VQCs are hybrid algorithms that merge a quantum circuit, which can be adjusted through parameters, with traditional classical optimization techniques. These circuits require only few qubits for effective learning. Recent studies have presented new ways of applying VQCs to reinforcement learning, showing promising results that warrant further exploration. This study investigates the effects of various techniques -- data re-uploading, input scaling, output scaling -- and introduces exponential learning rate decay in the quantum proximal policy optimization algorithm's actor-VQC. We assess these methods in the popular Frozen Lake and Cart Pole environments. Our focus is on their ability to reduce the number of parameters in the VQC without losing effectiveness. Our findings indicate that data re-uploading and an exponential learning rate decay significantly enhance hyperparameter stability and overall performance. While input scaling does not improve parameter efficiency, output scaling effectively manages greediness, leading to increased learning speed and robustness.
Weight Re-Mapping for Variational Quantum Algorithms
Jun 09, 2023Abstract:Inspired by the remarkable success of artificial neural networks across a broad spectrum of AI tasks, variational quantum circuits (VQCs) have recently seen an upsurge in quantum machine learning applications. The promising outcomes shown by VQCs, such as improved generalization and reduced parameter training requirements, are attributed to the robust algorithmic capabilities of quantum computing. However, the current gradient-based training approaches for VQCs do not adequately accommodate the fact that trainable parameters (or weights) are typically used as angles in rotational gates. To address this, we extend the concept of weight re-mapping for VQCs, as introduced by K\"olle et al. (2023). This approach unambiguously maps the weights to an interval of length $2\pi$, mirroring data rescaling techniques in conventional machine learning that have proven to be highly beneficial in numerous scenarios. In our study, we employ seven distinct weight re-mapping functions to assess their impact on eight classification datasets, using variational classifiers as a representative example. Our results indicate that weight re-mapping can enhance the convergence speed of the VQC. We assess the efficacy of various re-mapping functions across all datasets and measure their influence on the VQC's average performance. Our findings indicate that weight re-mapping not only consistently accelerates the convergence of VQCs, regardless of the specific re-mapping function employed, but also significantly increases accuracy in certain cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge