Emergent Cooperation in Quantum Multi-Agent Reinforcement Learning Using Communication

Emergent cooperation in classical Multi-Agent Reinforcement Learning has gained significant attention, particularly in the context of Sequential Social Dilemmas (SSDs). While classical reinforcement learning approaches have demonstrated capability for emergent cooperation, research on extending these methods to Quantum Multi-Agent Reinforcement Learning remains limited, particularly through communication. In this paper, we apply communication approaches to quantum Q-Learning agents: the Mutual Acknowledgment Token Exchange (MATE) protocol, its extension Mutually Endorsed Distributed Incentive Acknowledgment Token Exchange (MEDIATE), the peer rewarding mechanism Gifting, and Reinforced Inter-Agent Learning (RIAL). We evaluate these approaches in three SSDs: the Iterated Prisoner's Dilemma, Iterated Stag Hunt, and Iterated Game of Chicken. Our experimental results show that approaches using MATE with temporal-difference measure (MATE\textsubscript{TD}), AutoMATE, MEDIATE-I, and MEDIATE-S achieved high cooperation levels across all dilemmas, demonstrating that communication is a viable mechanism for fostering emergent cooperation in Quantum Multi-Agent Reinforcement Learning.

Quantum King-Ring Domination in Chess: A QAOA Approach

The Quantum Approximate Optimization Algorithm (QAOA) is extensively benchmarked on synthetic random instances such as MaxCut, TSP, and SAT problems, but these lack semantic structure and human interpretability, offering limited insight into performance on real-world problems with meaningful constraints. We introduce Quantum King-Ring Domination (QKRD), a NISQ-scale benchmark derived from chess tactical positions that provides 5,000 structured instances with one-hot constraints, spatial locality, and 10--40 qubit scale. The benchmark pairs human-interpretable coverage metrics with intrinsic validation against classical heuristics, enabling algorithmic conclusions without external oracles. Using QKRD, we systematically evaluate QAOA design choices and find that constraint-preserving mixers (XY, domain-wall) converge approximately 13 steps faster than standard mixers (p<10^{-7}, d\approx0.5) while eliminating penalty tuning, warm-start strategies reduce convergence by 45 steps (p<10^{-127}, d=3.35) with energy improvements exceeding d=8, and Conditional Value-at-Risk (CVaR) optimization yields an informative negative result with worse energy (p<10^{-40}, d=1.21) and no coverage benefit. Intrinsic validation shows QAOA outperforms greedy heuristics by 12.6\% and random selection by 80.1\%. Our results demonstrate that structured benchmarks reveal advantages of problem-informed QAOA techniques obscured in random instances. We release all code, data, and experimental artifacts for reproducible NISQ algorithm research.

Topology-Guided Quantum GANs for Constrained Graph Generation

Quantum computing (QC) promises theoretical advantages, benefiting computational problems that would not be efficiently classically simulatable. However, much of this theoretical speedup depends on the quantum circuit design solving the problem. We argue that QC literature has yet to explore more domain specific ansatz-topologies, instead of relying on generic, one-size-fits-all architectures. In this work, we show that incorporating task-specific inductive biases -- specifically geometric priors -- into quantum circuit design can enhance the performance of hybrid Quantum Generative Adversarial Networks (QuGANs) on the task of generating geometrically constrained K4 graphs. We evaluate a portfolio of entanglement topologies and loss-function designs to assess their impact on both statistical fidelity and compliance with geometric constraints, including the Triangle and Ptolemaic inequalities. Our results show that aligning circuit topology with the underlying problem structure yields substantial benefits: the Triangle-topology QuGAN achieves the highest geometric validity among quantum models and matches the performance of classical Generative Adversarial Networks (GAN). Additionally, we showcase how specific architectural choices, such as entangling gate types, variance regularization and output-scaling govern the trade-off between geometric consistency and distributional accuracy, thus emphasizing the value of structured, task-aware quantum ansatz-topologies.

Evaluating Mutation Techniques in Genetic Algorithm-Based Quantum Circuit Synthesis

Quantum computing leverages the unique properties of qubits and quantum parallelism to solve problems intractable for classical systems, offering unparalleled computational potential. However, the optimization of quantum circuits remains critical, especially for noisy intermediate-scale quantum (NISQ) devices with limited qubits and high error rates. Genetic algorithms (GAs) provide a promising approach for efficient quantum circuit synthesis by automating optimization tasks. This work examines the impact of various mutation strategies within a GA framework for quantum circuit synthesis. By analyzing how different mutations transform circuits, it identifies strategies that enhance efficiency and performance. Experiments utilized a fitness function emphasizing fidelity, while accounting for circuit depth and T operations, to optimize circuits with four to six qubits. Comprehensive hyperparameter testing revealed that combining delete and swap strategies outperformed other approaches, demonstrating their effectiveness in developing robust GA-based quantum circuit optimizers.

PIMAEX: Multi-Agent Exploration through Peer Incentivization

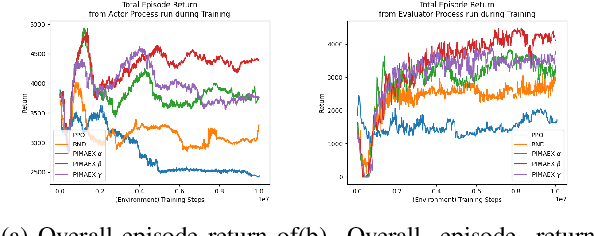
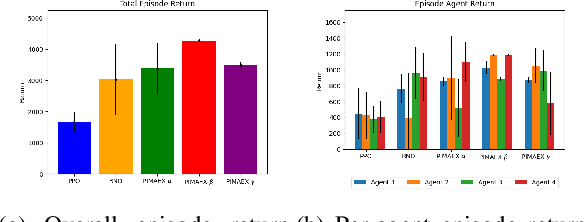
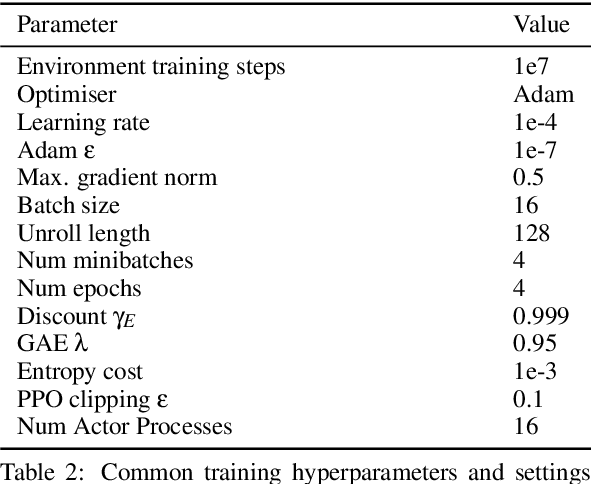
While exploration in single-agent reinforcement learning has been studied extensively in recent years, considerably less work has focused on its counterpart in multi-agent reinforcement learning. To address this issue, this work proposes a peer-incentivized reward function inspired by previous research on intrinsic curiosity and influence-based rewards. The \textit{PIMAEX} reward, short for Peer-Incentivized Multi-Agent Exploration, aims to improve exploration in the multi-agent setting by encouraging agents to exert influence over each other to increase the likelihood of encountering novel states. We evaluate the \textit{PIMAEX} reward in conjunction with \textit{PIMAEX-Communication}, a multi-agent training algorithm that employs a communication channel for agents to influence one another. The evaluation is conducted in the \textit{Consume/Explore} environment, a partially observable environment with deceptive rewards, specifically designed to challenge the exploration vs.\ exploitation dilemma and the credit-assignment problem. The results empirically demonstrate that agents using the \textit{PIMAEX} reward with \textit{PIMAEX-Communication} outperform those that do not.

Optimizing Sensor Redundancy in Sequential Decision-Making Problems

Reinforcement Learning (RL) policies are designed to predict actions based on current observations to maximize cumulative future rewards. In real-world applications (i.e., non-simulated environments), sensors are essential for measuring the current state and providing the observations on which RL policies rely to make decisions. A significant challenge in deploying RL policies in real-world scenarios is handling sensor dropouts, which can result from hardware malfunctions, physical damage, or environmental factors like dust on a camera lens. A common strategy to mitigate this issue is the use of backup sensors, though this comes with added costs. This paper explores the optimization of backup sensor configurations to maximize expected returns while keeping costs below a specified threshold, C. Our approach uses a second-order approximation of expected returns and includes penalties for exceeding cost constraints. We then optimize this quadratic program using Tabu Search, a meta-heuristic algorithm. The approach is evaluated across eight OpenAI Gym environments and a custom Unity-based robotic environment (RobotArmGrasping). Empirical results demonstrate that our quadratic program effectively approximates real expected returns, facilitating the identification of optimal sensor configurations.

A Study on Optimization Techniques for Variational Quantum Circuits in Reinforcement Learning

Quantum Computing aims to streamline machine learning, making it more effective with fewer trainable parameters. This reduction of parameters can speed up the learning process and reduce the use of computational resources. However, in the current phase of quantum computing development, known as the noisy intermediate-scale quantum era (NISQ), learning is difficult due to a limited number of qubits and widespread quantum noise. To overcome these challenges, researchers are focusing on variational quantum circuits (VQCs). VQCs are hybrid algorithms that merge a quantum circuit, which can be adjusted through parameters, with traditional classical optimization techniques. These circuits require only few qubits for effective learning. Recent studies have presented new ways of applying VQCs to reinforcement learning, showing promising results that warrant further exploration. This study investigates the effects of various techniques -- data re-uploading, input scaling, output scaling -- and introduces exponential learning rate decay in the quantum proximal policy optimization algorithm's actor-VQC. We assess these methods in the popular Frozen Lake and Cart Pole environments. Our focus is on their ability to reduce the number of parameters in the VQC without losing effectiveness. Our findings indicate that data re-uploading and an exponential learning rate decay significantly enhance hyperparameter stability and overall performance. While input scaling does not improve parameter efficiency, output scaling effectively manages greediness, leading to increased learning speed and robustness.

Qandle: Accelerating State Vector Simulation Using Gate-Matrix Caching and Circuit Splitting

To address the computational complexity associated with state-vector simulation for quantum circuits, we propose a combination of advanced techniques to accelerate circuit execution. Quantum gate matrix caching reduces the overhead of repeated applications of the Kronecker product when applying a gate matrix to the state vector by storing decomposed partial matrices for each gate. Circuit splitting divides the circuit into sub-circuits with fewer gates by constructing a dependency graph, enabling parallel or sequential execution on disjoint subsets of the state vector. These techniques are implemented using the PyTorch machine learning framework. We demonstrate the performance of our approach by comparing it to other PyTorch-compatible quantum state-vector simulators. Our implementation, named Qandle, is designed to seamlessly integrate with existing machine learning workflows, providing a user-friendly API and compatibility with the OpenQASM format. Qandle is an open-source project hosted on GitHub https://github.com/gstenzel/qandle and PyPI https://pypi.org/project/qandle/ .

Quantum Denoising Diffusion Models

In recent years, machine learning models like DALL-E, Craiyon, and Stable Diffusion have gained significant attention for their ability to generate high-resolution images from concise descriptions. Concurrently, quantum computing is showing promising advances, especially with quantum machine learning which capitalizes on quantum mechanics to meet the increasing computational requirements of traditional machine learning algorithms. This paper explores the integration of quantum machine learning and variational quantum circuits to augment the efficacy of diffusion-based image generation models. Specifically, we address two challenges of classical diffusion models: their low sampling speed and the extensive parameter requirements. We introduce two quantum diffusion models and benchmark their capabilities against their classical counterparts using MNIST digits, Fashion MNIST, and CIFAR-10. Our models surpass the classical models with similar parameter counts in terms of performance metrics FID, SSIM, and PSNR. Moreover, we introduce a consistency model unitary single sampling architecture that combines the diffusion procedure into a single step, enabling a fast one-step image generation.