A Survey of Methods for Converting Unstructured Data to CSG Models

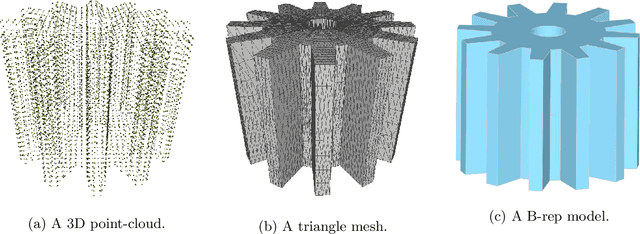
The goal of this document is to survey existing methods for recovering CSG representations from unstructured data such as 3D point-clouds or polygon meshes. We review and discuss related topics such as the segmentation and fitting of the input data. We cover techniques from solid modeling and CAD for polyhedron to CSG and B-rep to CSG conversion. We look at approaches coming from program synthesis, evolutionary techniques (such as genetic programming or genetic algorithm), and deep learning methods. Finally, we conclude with a discussion of techniques for the generation of computer programs representing solids (not just CSG models) and higher-level representations (such as, for example, the ones based on sketch and extrusion or feature based operations).

Solving Large Steiner Tree Problems in Graphs for Cost-Efficient Fiber-To-The-Home Network Expansion

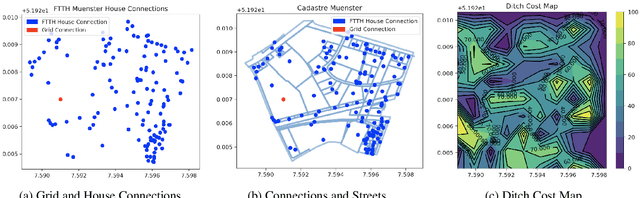
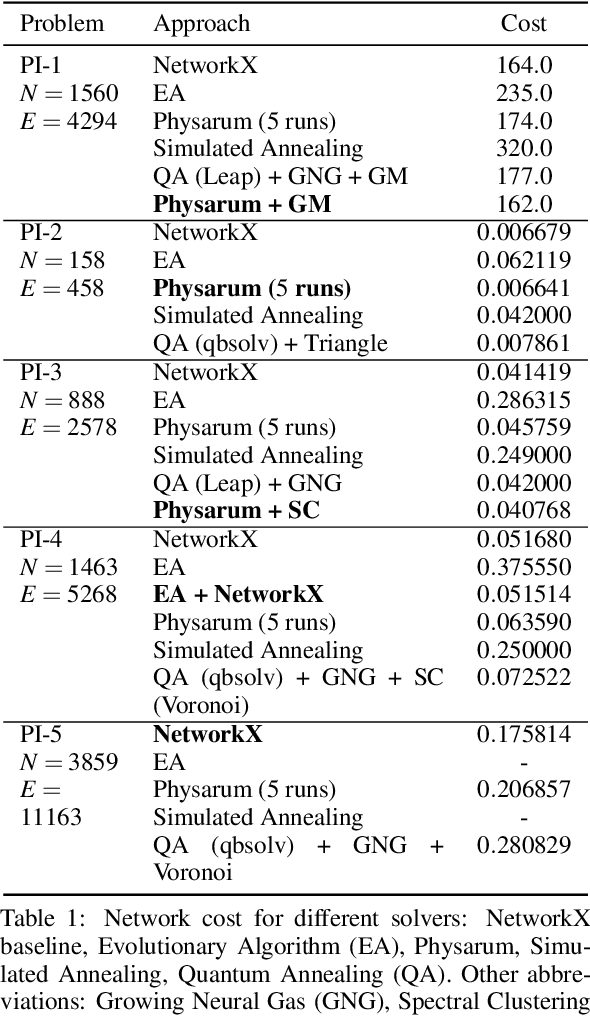
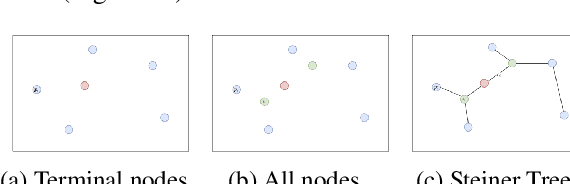
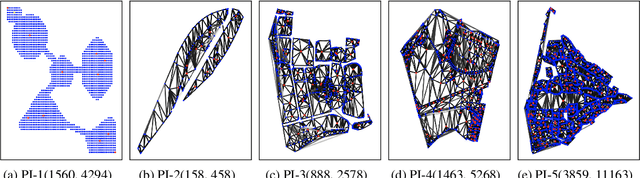
The expansion of Fiber-To-The-Home (FTTH) networks creates high costs due to expensive excavation procedures. Optimizing the planning process and minimizing the cost of the earth excavation work therefore lead to large savings. Mathematically, the FTTH network problem can be described as a minimum Steiner Tree problem. Even though the Steiner Tree problem has already been investigated intensively in the last decades, it might be further optimized with the help of new computing paradigms and emerging approaches. This work studies upcoming technologies, such as Quantum Annealing, Simulated Annealing and nature-inspired methods like Evolutionary Algorithms or slime-mold-based optimization. Additionally, we investigate partitioning and simplifying methods. Evaluated on several real-life problem instances, we could outperform a traditional, widely-used baseline (NetworkX Approximate Solver) on most of the domains. Prior partitioning of the initial graph and the presented slime-mold-based approach were especially valuable for a cost-efficient approximation. Quantum Annealing seems promising, but was limited by the number of available qubits.

Reconstruction of Convex Polytope Compositions from 3D Point-clouds

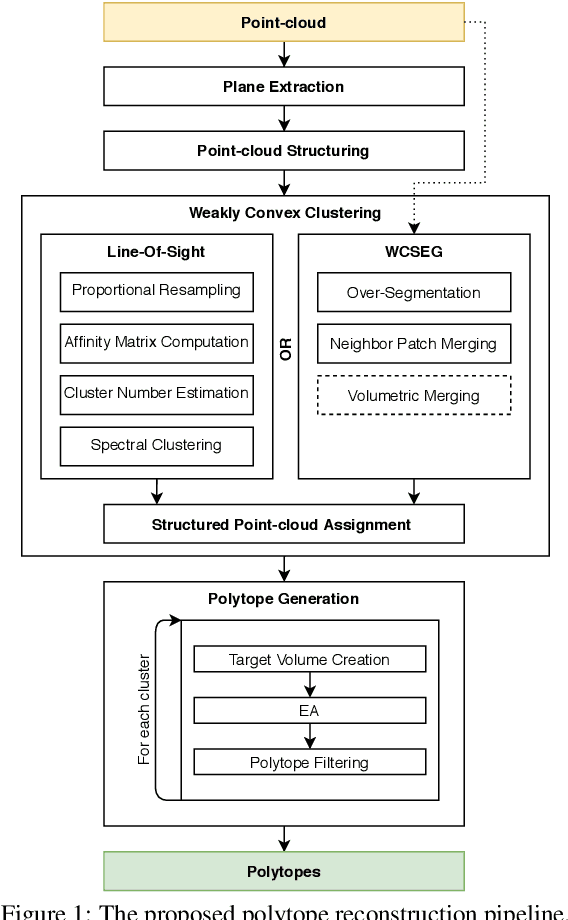
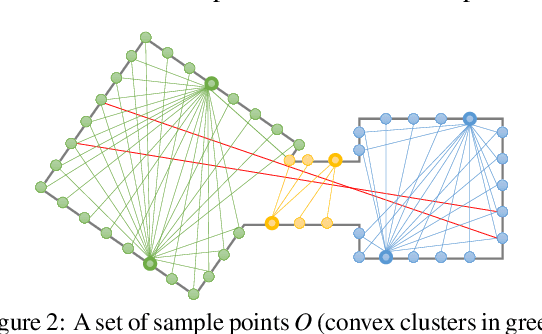
Reconstructing a composition (union) of convex polytopes that perfectly fits the corresponding input point-cloud is a hard optimization problem with interesting applications in reverse engineering and rigid body dynamics simulations. We propose a pipeline that first extracts a set of planes, then partitions the input point-cloud into weakly convex clusters and finally generates a set of convex polytopes as the intersection of fitted planes for each partition. Finding the best-fitting convex polytopes is formulated as a combinatorial optimization problem over the set of fitted planes and is solved using an Evolutionary Algorithm. For convex clustering, we employ two different methods and detail their strengths and weaknesses in a thorough evaluation based on multiple input data-sets.

A Flexible Pipeline for the Optimization of CSG Trees

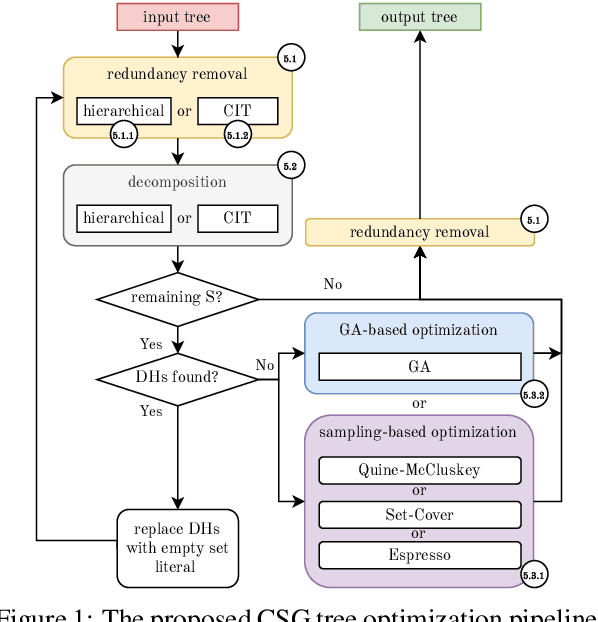
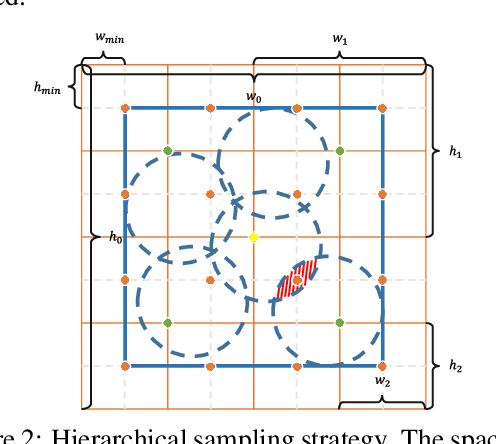
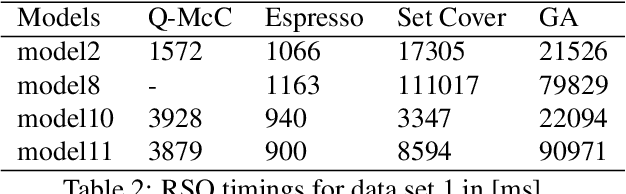
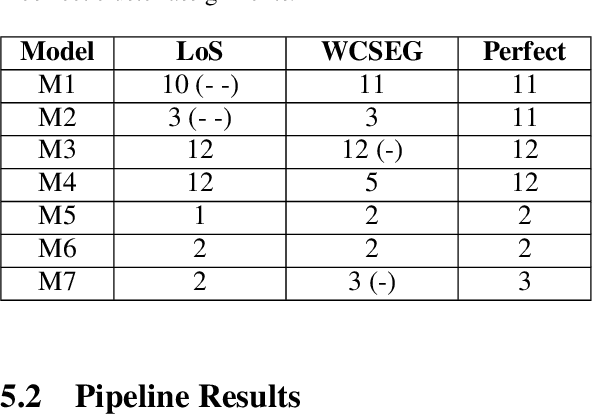
CSG trees are an intuitive, yet powerful technique for the representation of geometry using a combination of Boolean set-operations and geometric primitives. In general, there exists an infinite number of trees all describing the same 3D solid. However, some trees are optimal regarding the number of used operations, their shape or other attributes, like their suitability for intuitive, human-controlled editing. In this paper, we present a systematic comparison of newly developed and existing tree optimization methods and propose a flexible processing pipeline with a focus on tree editability. The pipeline uses a redundancy removal and decomposition stage for complexity reduction and different (meta-)heuristics for remaining tree optimization. We also introduce a new quantitative measure for CSG tree editability and show how it can be used as a constraint in the optimization process.

Accelerating Evolutionary Construction Tree Extraction via Graph Partitioning

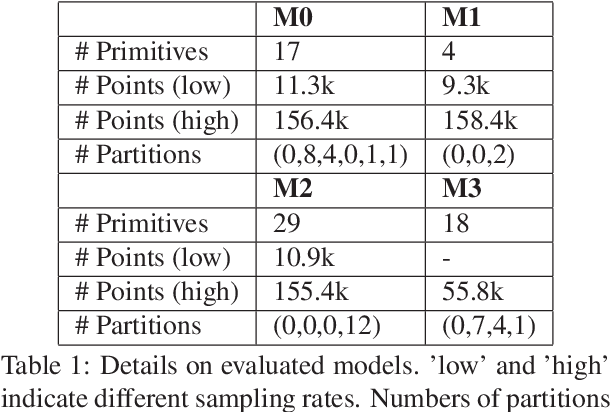
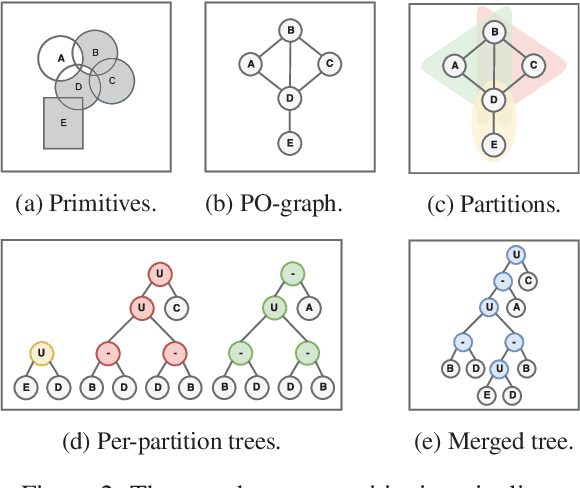
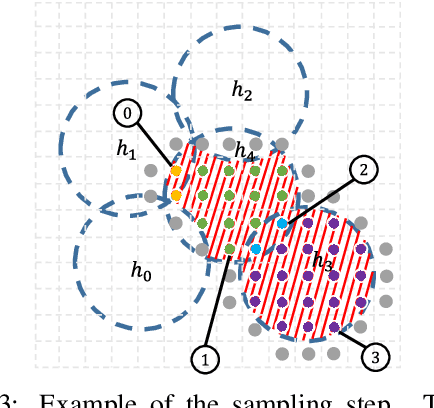
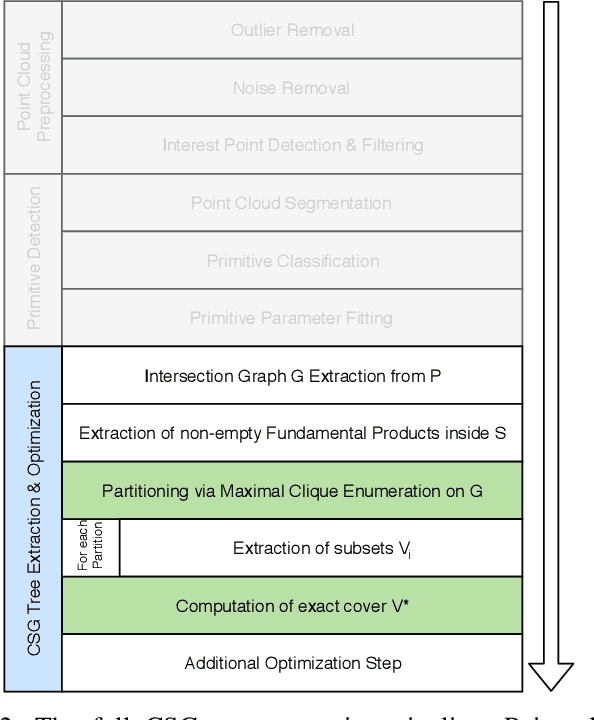
Extracting a Construction Tree from potentially noisy point clouds is an important aspect of Reverse Engineering tasks in Computer Aided Design. Solutions based on algorithmic geometry impose constraints on usable model representations (e.g. quadric surfaces only) and noise robustness. Re-formulating the problem as a combinatorial optimization problem and solving it with an Evolutionary Algorithm can mitigate some of these constraints at the cost of increased computational complexity. This paper proposes a graph-based search space partitioning scheme that is able to accelerate Evolutionary Construction Tree extraction while exploiting parallelization capabilities of modern CPUs. The evaluation indicates a speed-up up to a factor of $46.6$ compared to the baseline approach while resulting tree sizes increased by $25.2\%$ to $88.6\%$.

Bayesian Surprise in Indoor Environments

This paper proposes a novel method to identify unexpected structures in 2D floor plans using the concept of Bayesian Surprise. Taking into account that a person's expectation is an important aspect of the perception of space, we exploit the theory of Bayesian Surprise to robustly model expectation and thus surprise in the context of building structures. We use Isovist Analysis, which is a popular space syntax technique, to turn qualitative object attributes into quantitative environmental information. Since isovists are location-specific patterns of visibility, a sequence of isovists describes the spatial perception during a movement along multiple points in space. We then use Bayesian Surprise in a feature space consisting of these isovist readings. To demonstrate the suitability of our approach, we take "snapshots" of an agent's local environment to provide a short list of images that characterize a traversed trajectory through a 2D indoor environment. Those fingerprints represent surprising regions of a tour, characterize the traversed map and enable indoor LBS to focus more on important regions. Given this idea, we propose to use "surprise" as a new dimension of context in indoor location-based services (LBS). Agents of LBS, such as mobile robots or non-player characters in computer games, may use the context surprise to focus more on important regions of a map for a better use or understanding of the floor plan.

Optimizing Geometry Compression using Quantum Annealing

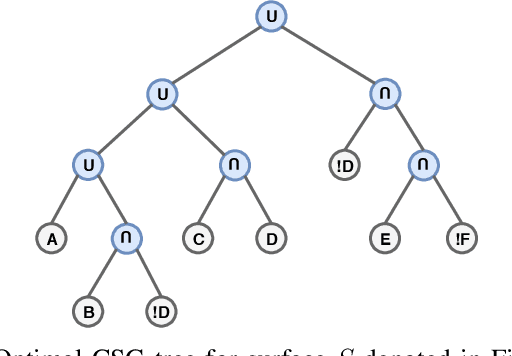
The compression of geometry data is an important aspect of bandwidth-efficient data transfer for distributed 3d computer vision applications. We propose a quantum-enabled lossy 3d point cloud compression pipeline based on the constructive solid geometry (CSG) model representation. Key parts of the pipeline are mapped to NP-complete problems for which an efficient Ising formulation suitable for the execution on a Quantum Annealer exists. We describe existing Ising formulations for the maximum clique search problem and the smallest exact cover problem, both of which are important building blocks of the proposed compression pipeline. Additionally, we discuss the properties of the overall pipeline regarding result optimality and described Ising formulations.

Memory Bounded Open-Loop Planning in Large POMDPs using Thompson Sampling

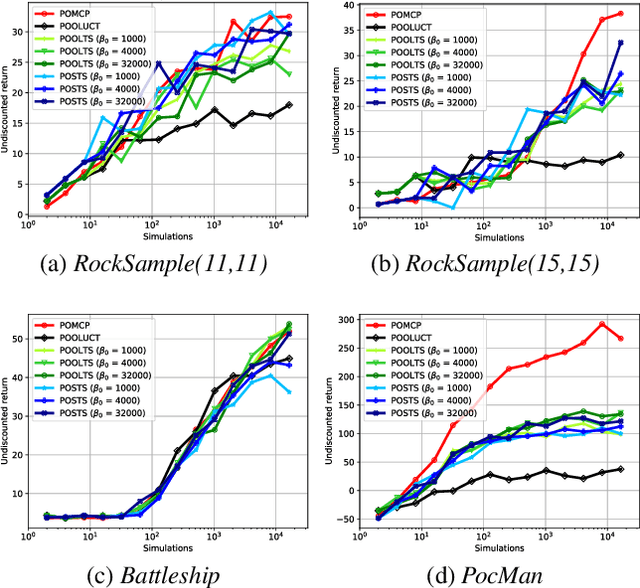
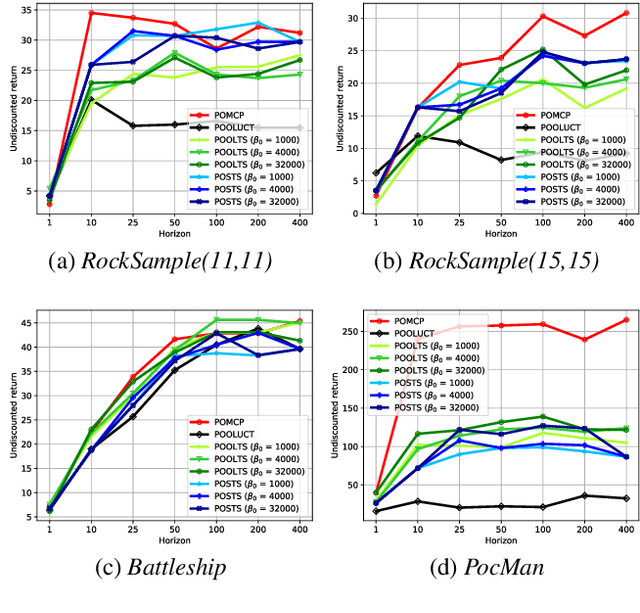
State-of-the-art approaches to partially observable planning like POMCP are based on stochastic tree search. While these approaches are computationally efficient, they may still construct search trees of considerable size, which could limit the performance due to restricted memory resources. In this paper, we propose Partially Observable Stacked Thompson Sampling (POSTS), a memory bounded approach to open-loop planning in large POMDPs, which optimizes a fixed size stack of Thompson Sampling bandits. We empirically evaluate POSTS in four large benchmark problems and compare its performance with different tree-based approaches. We show that POSTS achieves competitive performance compared to tree-based open-loop planning and offers a performance-memory tradeoff, making it suitable for partially observable planning with highly restricted computational and memory resources.