Pierre-Alain Fayolle
Accuracy Improvements for Convolutional and Differential Distance Function Approximations
Dec 12, 2024Abstract:Given a bounded domain, we deal with the problem of estimating the distance function from the internal points of the domain to the boundary of the domain. Convolutional and differential distance estimation schemes are considered and, for both the schemes, accuracy improvements are proposed and evaluated. Asymptotics of Laplace integrals and Taylor series extrapolations are used to achieve the improvements.
A Survey of Methods for Converting Unstructured Data to CSG Models
May 02, 2023
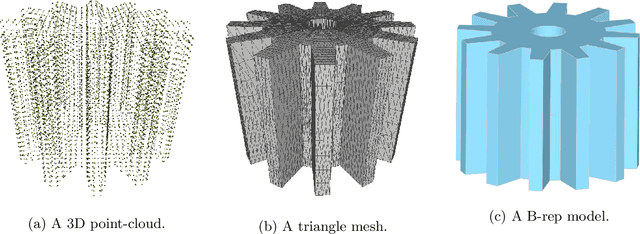
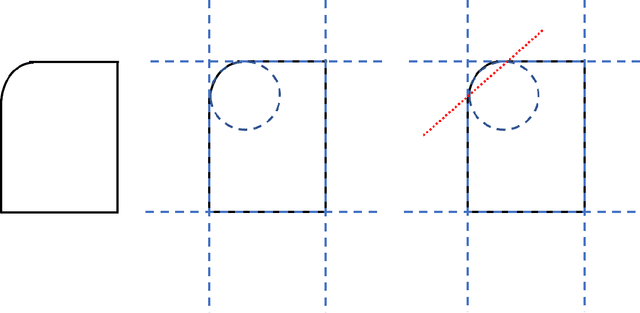
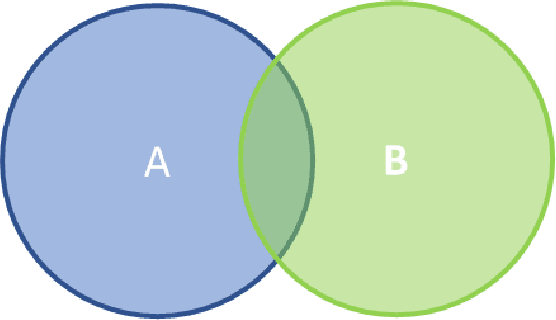
Abstract:The goal of this document is to survey existing methods for recovering CSG representations from unstructured data such as 3D point-clouds or polygon meshes. We review and discuss related topics such as the segmentation and fitting of the input data. We cover techniques from solid modeling and CAD for polyhedron to CSG and B-rep to CSG conversion. We look at approaches coming from program synthesis, evolutionary techniques (such as genetic programming or genetic algorithm), and deep learning methods. Finally, we conclude with a discussion of techniques for the generation of computer programs representing solids (not just CSG models) and higher-level representations (such as, for example, the ones based on sketch and extrusion or feature based operations).
Reconstruction of Convex Polytope Compositions from 3D Point-clouds
Apr 27, 2021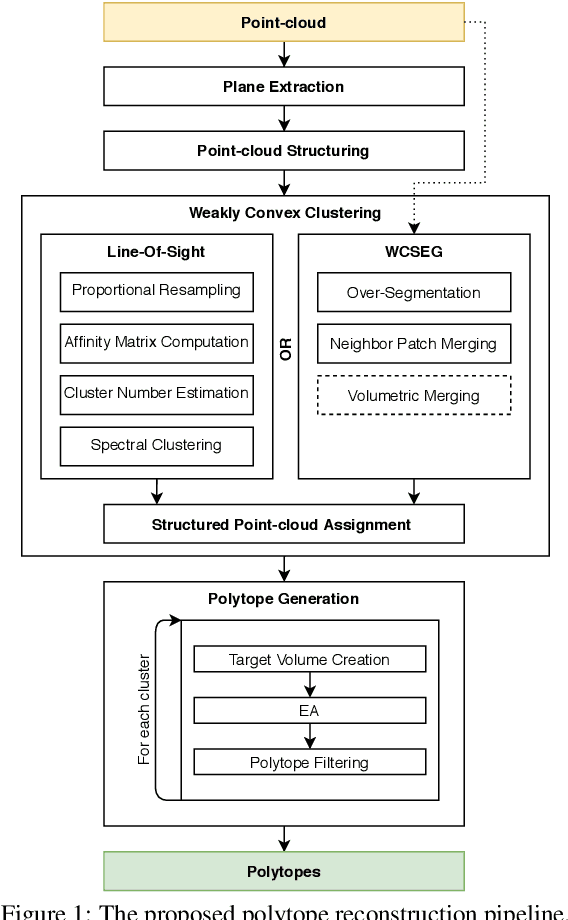
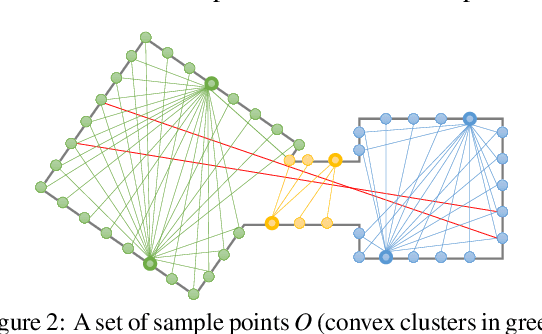

Abstract:Reconstructing a composition (union) of convex polytopes that perfectly fits the corresponding input point-cloud is a hard optimization problem with interesting applications in reverse engineering and rigid body dynamics simulations. We propose a pipeline that first extracts a set of planes, then partitions the input point-cloud into weakly convex clusters and finally generates a set of convex polytopes as the intersection of fitted planes for each partition. Finding the best-fitting convex polytopes is formulated as a combinatorial optimization problem over the set of fitted planes and is solved using an Evolutionary Algorithm. For convex clustering, we employ two different methods and detail their strengths and weaknesses in a thorough evaluation based on multiple input data-sets.
Signed Distance Function Computation from an Implicit Surface
Apr 16, 2021



Abstract:We describe in this short note a technique to convert an implicit surface into a Signed Distance Function (SDF) while exactly preserving the zero level-set of the implicit. The proposed approach relies on embedding the input implicit in the final layer of a neural network, which is trained to minimize a loss function characterizing the SDF.
A Flexible Pipeline for the Optimization of CSG Trees
Sep 12, 2020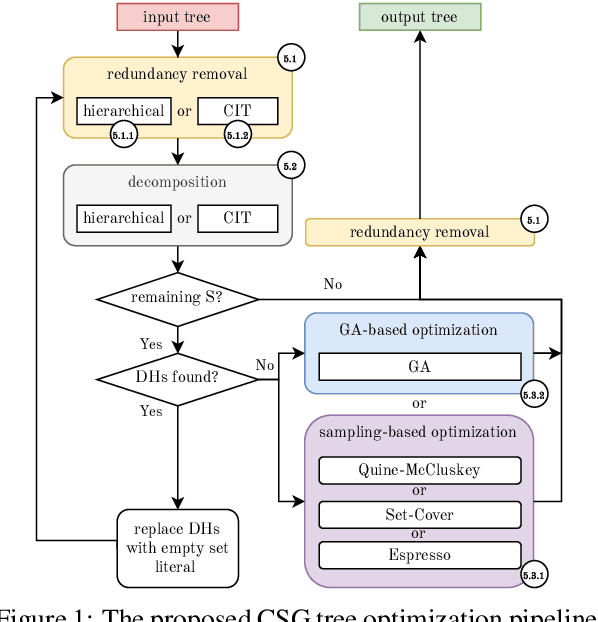
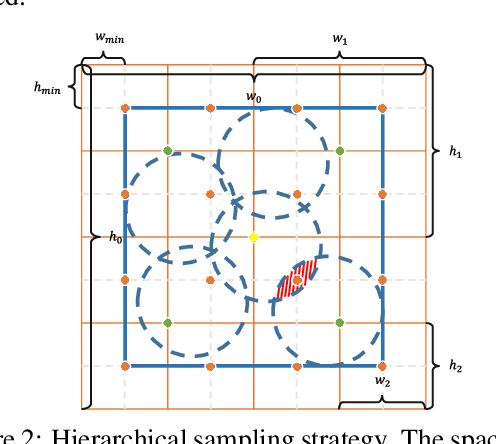
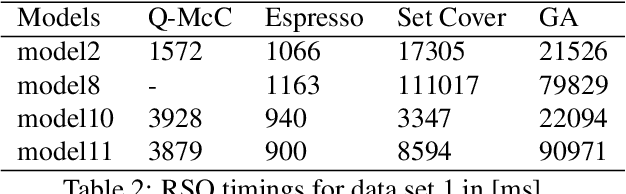
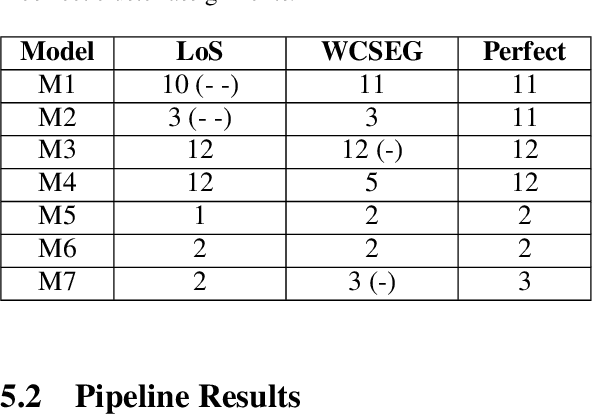
Abstract:CSG trees are an intuitive, yet powerful technique for the representation of geometry using a combination of Boolean set-operations and geometric primitives. In general, there exists an infinite number of trees all describing the same 3D solid. However, some trees are optimal regarding the number of used operations, their shape or other attributes, like their suitability for intuitive, human-controlled editing. In this paper, we present a systematic comparison of newly developed and existing tree optimization methods and propose a flexible processing pipeline with a focus on tree editability. The pipeline uses a redundancy removal and decomposition stage for complexity reduction and different (meta-)heuristics for remaining tree optimization. We also introduce a new quantitative measure for CSG tree editability and show how it can be used as a constraint in the optimization process.
Accelerating Evolutionary Construction Tree Extraction via Graph Partitioning
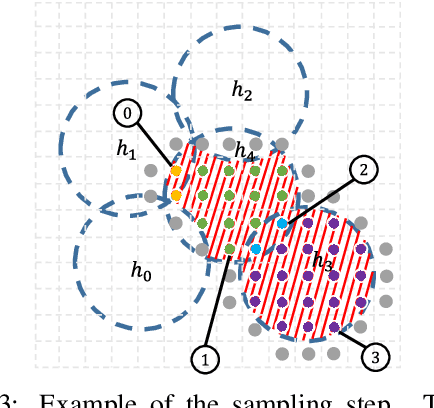
Aug 09, 2020
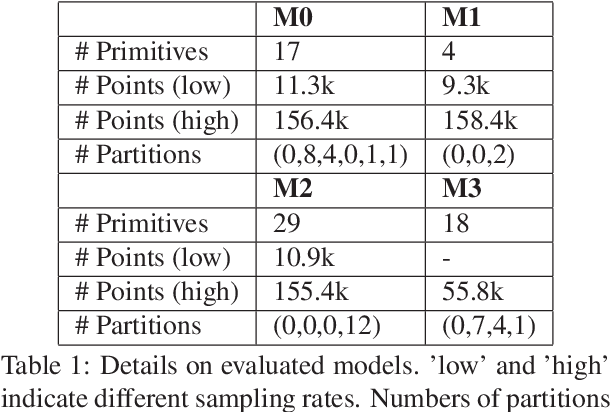
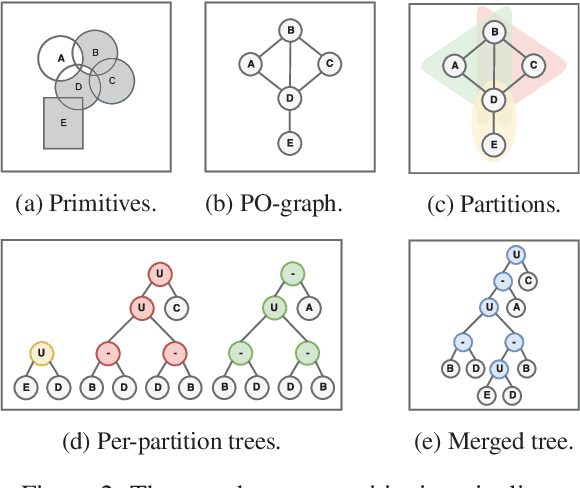
Abstract:Extracting a Construction Tree from potentially noisy point clouds is an important aspect of Reverse Engineering tasks in Computer Aided Design. Solutions based on algorithmic geometry impose constraints on usable model representations (e.g. quadric surfaces only) and noise robustness. Re-formulating the problem as a combinatorial optimization problem and solving it with an Evolutionary Algorithm can mitigate some of these constraints at the cost of increased computational complexity. This paper proposes a graph-based search space partitioning scheme that is able to accelerate Evolutionary Construction Tree extraction while exploiting parallelization capabilities of modern CPUs. The evaluation indicates a speed-up up to a factor of $46.6$ compared to the baseline approach while resulting tree sizes increased by $25.2\%$ to $88.6\%$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge