ROCK: A variational formulation for occupation kernel methods in Reproducing Kernel Hilbert Spaces

We present a Representer Theorem result for a large class of weak formulation problems. We provide examples of applications of our formulation both in traditional machine learning and numerical methods as well as in new and emerging techniques. Finally we apply our formulation to generalize the multivariate occupation kernel (MOCK) method for learning dynamical systems from data proposing the more general Riesz Occupation Kernel (ROCK) method. Our generalized methods are both more computationally efficient and performant on most of the benchmarks we test against.

The Stochastic Occupation Kernel Method for System Identification

The method of occupation kernels has been used to learn ordinary differential equations from data in a non-parametric way. We propose a two-step method for learning the drift and diffusion of a stochastic differential equation given snapshots of the process. In the first step, we learn the drift by applying the occupation kernel algorithm to the expected value of the process. In the second step, we learn the diffusion given the drift using a semi-definite program. Specifically, we learn the diffusion squared as a non-negative function in a RKHS associated with the square of a kernel. We present examples and simulations.

A Finite-Horizon Approach to Active Level Set Estimation

We consider the problem of active learning in the context of spatial sampling for level set estimation (LSE), where the goal is to localize all regions where a function of interest lies above/below a given threshold as quickly as possible. We present a finite-horizon search procedure to perform LSE in one dimension while optimally balancing both the final estimation error and the distance traveled for a fixed number of samples. A tuning parameter is used to trade off between the estimation accuracy and distance traveled. We show that the resulting optimization problem can be solved in closed form and that the resulting policy generalizes existing approaches to this problem. We then show how this approach can be used to perform level set estimation in higher dimensions under the popular Gaussian process model. Empirical results on synthetic data indicate that as the cost of travel increases, our method's ability to treat distance nonmyopically allows it to significantly improve on the state of the art. On real air quality data, our approach achieves roughly one fifth the estimation error at less than half the cost of competing algorithms.

Learning High-Dimensional Nonparametric Differential Equations via Multivariate Occupation Kernel Functions

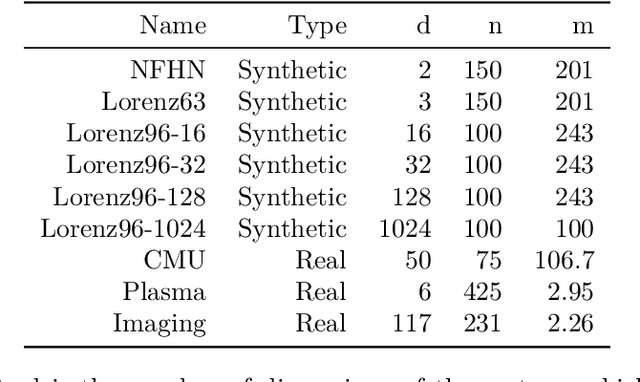
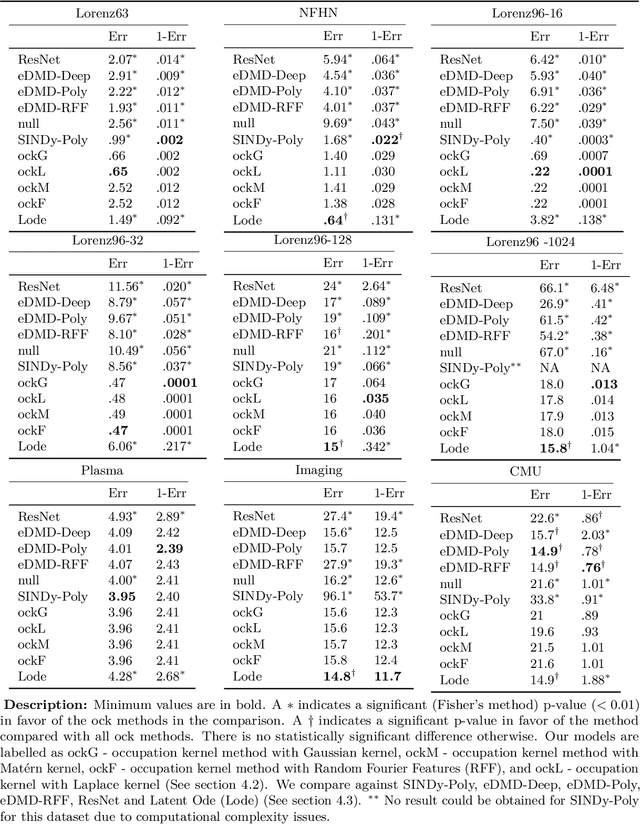
Learning a nonparametric system of ordinary differential equations (ODEs) from $n$ trajectory snapshots in a $d$-dimensional state space requires learning $d$ functions of $d$ variables. Explicit formulations scale quadratically in $d$ unless additional knowledge about system properties, such as sparsity and symmetries, is available. In this work, we propose a linear approach to learning using the implicit formulation provided by vector-valued Reproducing Kernel Hilbert Spaces. By rewriting the ODEs in a weaker integral form, which we subsequently minimize, we derive our learning algorithm. The minimization problem's solution for the vector field relies on multivariate occupation kernel functions associated with the solution trajectories. We validate our approach through experiments on highly nonlinear simulated and real data, where $d$ may exceed 100. We further demonstrate the versatility of the proposed method by learning a nonparametric first order quasilinear partial differential equation.

Learning Nonparametric Ordinary differential Equations: Application to Sparse and Noisy Data

Learning nonparametric systems of Ordinary Differential Equations (ODEs) $\dot x = f(t,x)$ from noisy and sparse data is an emerging machine learning topic. We use the well-developed theory of Reproducing Kernel Hilbert Spaces (RKHS) to define candidates for $f$ for which the solution of the ODE exists and is unique. Learning $f$ consists of solving a constrained optimization problem in an RKHS. We propose a penalty method that iteratively uses the Representer theorem and Euler approximations to provide a numerical solution. We prove a generalization bound for the $L^2$ distance between $x$ and its estimator. Experiments are provided for the FitzHugh Nagumo oscillator and for the prediction of the Amyloid level in the cortex of aging subjects. In both cases, we show competitive results when compared with the state of the art.

Machine Learning for Health (ML4H) Workshop at NeurIPS 2018

This volume represents the accepted submissions from the Machine Learning for Health (ML4H) workshop at the conference on Neural Information Processing Systems (NeurIPS) 2018, held on December 8, 2018 in Montreal, Canada.

Gaussian Processes with Context-Supported Priors for Active Object Localization

We devise an algorithm using a Bayesian optimization framework in conjunction with contextual visual data for the efficient localization of objects in still images. Recent research has demonstrated substantial progress in object localization and related tasks for computer vision. However, many current state-of-the-art object localization procedures still suffer from inaccuracy and inefficiency, in addition to failing to provide a principled and interpretable system amenable to high-level vision tasks. We address these issues with the current research. Our method encompasses an active search procedure that uses contextual data to generate initial bounding-box proposals for a target object. We train a convolutional neural network to approximate an offset distance from the target object. Next, we use a Gaussian Process to model this offset response signal over the search space of the target. We then employ a Bayesian active search for accurate localization of the target. In experiments, we compare our approach to a state-of-theart bounding-box regression method for a challenging pedestrian localization task. Our method exhibits a substantial improvement over this baseline regression method.

Non-Adaptive Policies for 20 Questions Target Localization

The problem of target localization with noise is addressed. The target is a sample from a continuous random variable with known distribution and the goal is to locate it with minimum mean squared error distortion. The localization scheme or policy proceeds by queries, or questions, weather or not the target belongs to some subset as it is addressed in the 20-question framework. These subsets are not constrained to be intervals and the answers to the queries are noisy. While this situation is well studied for adaptive querying, this paper is focused on the non adaptive querying policies based on dyadic questions. The asymptotic minimum achievable distortion under such policies is derived. Furthermore, a policy named the Aurelian1 is exhibited which achieves asymptotically this distortion.

Active Testing for Face Detection and Localization

We provide a novel search technique, which uses a hierarchical model and a mutual information gain heuristic to efficiently prune the search space when localizing faces in images. We show exponential gains in computation over traditional sliding window approaches, while keeping similar performance levels.