A Finite-Horizon Approach to Active Level Set Estimation

We consider the problem of active learning in the context of spatial sampling for level set estimation (LSE), where the goal is to localize all regions where a function of interest lies above/below a given threshold as quickly as possible. We present a finite-horizon search procedure to perform LSE in one dimension while optimally balancing both the final estimation error and the distance traveled for a fixed number of samples. A tuning parameter is used to trade off between the estimation accuracy and distance traveled. We show that the resulting optimization problem can be solved in closed form and that the resulting policy generalizes existing approaches to this problem. We then show how this approach can be used to perform level set estimation in higher dimensions under the popular Gaussian process model. Empirical results on synthetic data indicate that as the cost of travel increases, our method's ability to treat distance nonmyopically allows it to significantly improve on the state of the art. On real air quality data, our approach achieves roughly one fifth the estimation error at less than half the cost of competing algorithms.

Subspace Clustering using Ensembles of $K$-Subspaces

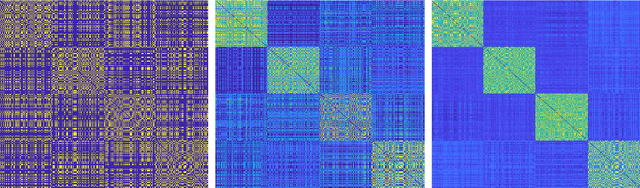
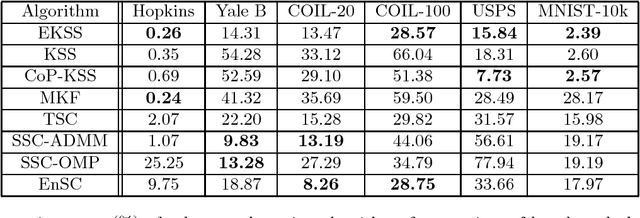
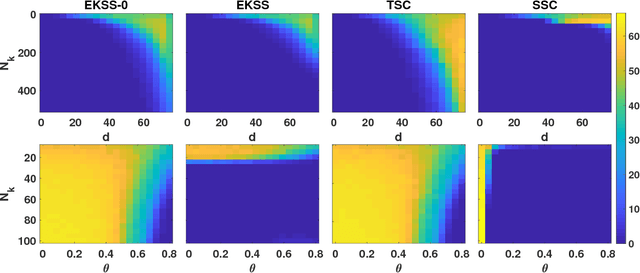
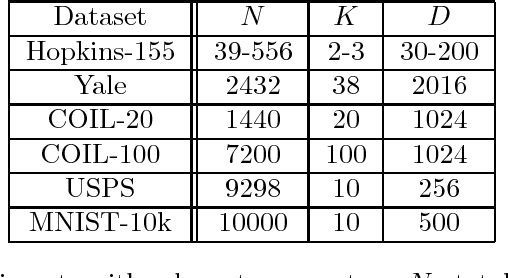
Subspace clustering is the unsupervised grouping of points lying near a union of low-dimensional linear subspaces. Algorithms based directly on geometric properties of such data tend to either provide poor empirical performance, lack theoretical guarantees, or depend heavily on their initialization. We present a novel geometric approach to the subspace clustering problem that leverages ensembles of the K-subspaces (KSS) algorithm via the evidence accumulation clustering framework. Our algorithm, referred to as ensemble K-subspaces (EKSS), forms a co-association matrix whose (i,j)th entry is the number of times points i and j are clustered together by several runs of KSS with random initializations. We prove general recovery guarantees for any algorithm that forms an affinity matrix with entries close to a monotonic transformation of pairwise absolute inner products. We then show that a specific instance of EKSS results in an affinity matrix with entries of this form, and hence our proposed algorithm can provably recover subspaces under similar conditions to state-of-the-art algorithms. The finding is, to the best of our knowledge, the first recovery guarantee for evidence accumulation clustering and for KSS variants. We show on synthetic data that our method performs well in the traditionally challenging settings of subspaces with large intersection, subspaces with small principal angles, and noisy data. Finally, we evaluate our algorithm on six common benchmark datasets and show that unlike existing methods, EKSS achieves excellent empirical performance when there are both a small and large number of points per subspace.

Leveraging Union of Subspace Structure to Improve Constrained Clustering

Many clustering problems in computer vision and other contexts are also classification problems, where each cluster shares a meaningful label. Subspace clustering algorithms in particular are often applied to problems that fit this description, for example with face images or handwritten digits. While it is straightforward to request human input on these datasets, our goal is to reduce this input as much as possible. We present a pairwise-constrained clustering algorithm that actively selects queries based on the union-of-subspaces model. The central step of the algorithm is in querying points of minimum margin between estimated subspaces; analogous to classifier margin, these lie near the decision boundary. We prove that points lying near the intersection of subspaces are points with low margin. Our procedure can be used after any subspace clustering algorithm that outputs an affinity matrix. We demonstrate on several datasets that our algorithm drives the clustering error down considerably faster than the state-of-the-art active query algorithms on datasets with subspace structure and is competitive on other datasets.

Distance-Penalized Active Learning Using Quantile Search

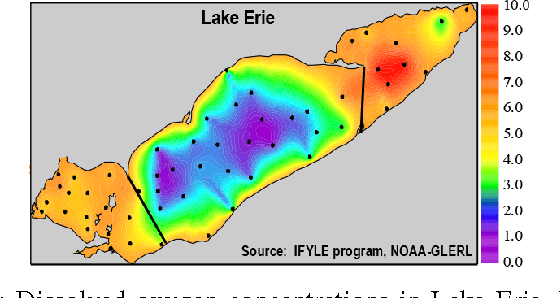
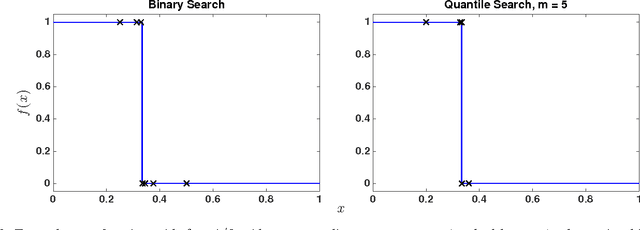
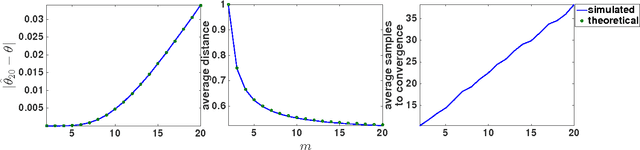
Adaptive sampling theory has shown that, with proper assumptions on the signal class, algorithms exist to reconstruct a signal in $\mathbb{R}^{d}$ with an optimal number of samples. We generalize this problem to the case of spatial signals, where the sampling cost is a function of both the number of samples taken and the distance traveled during estimation. This is motivated by our work studying regions of low oxygen concentration in the Great Lakes. We show that for one-dimensional threshold classifiers, a tradeoff between the number of samples taken and distance traveled can be achieved using a generalization of binary search, which we refer to as quantile search. We characterize both the estimation error after a fixed number of samples and the distance traveled in the noiseless case, as well as the estimation error in the case of noisy measurements. We illustrate our results in both simulations and experiments and show that our method outperforms existing algorithms in the majority of practical scenarios.