Distance-Penalized Active Learning Using Quantile Search
Paper and Code
Feb 16, 2017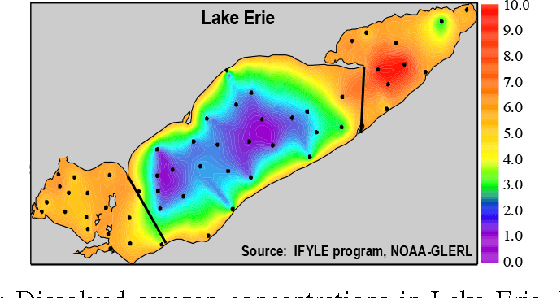
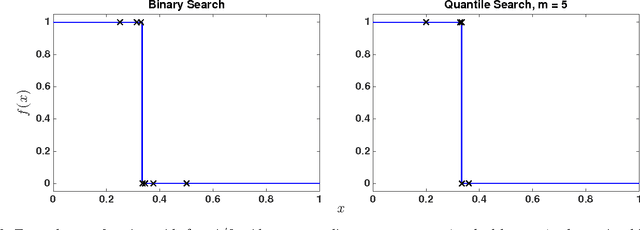
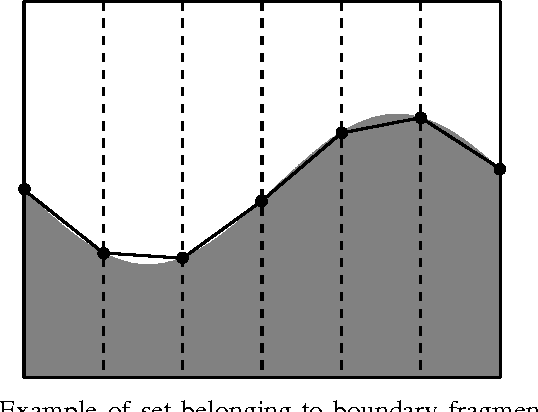
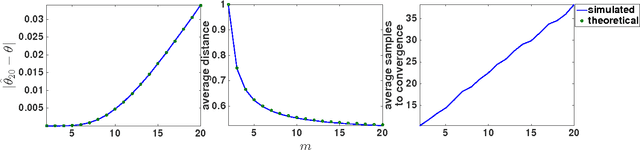
Adaptive sampling theory has shown that, with proper assumptions on the signal class, algorithms exist to reconstruct a signal in $\mathbb{R}^{d}$ with an optimal number of samples. We generalize this problem to the case of spatial signals, where the sampling cost is a function of both the number of samples taken and the distance traveled during estimation. This is motivated by our work studying regions of low oxygen concentration in the Great Lakes. We show that for one-dimensional threshold classifiers, a tradeoff between the number of samples taken and distance traveled can be achieved using a generalization of binary search, which we refer to as quantile search. We characterize both the estimation error after a fixed number of samples and the distance traveled in the noiseless case, as well as the estimation error in the case of noisy measurements. We illustrate our results in both simulations and experiments and show that our method outperforms existing algorithms in the majority of practical scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge