Identification of stormwater control strategies and their associated uncertainties using Bayesian Optimization

Dynamic control is emerging as an effective methodology for operating stormwater systems under stress from rapidly evolving weather patterns. Informed by rainfall predictions and real-time sensor measurements, control assets in the stormwater network can be dynamically configured to tune the behavior of the stormwater network to reduce the risk of urban flooding, equalize flows to the water reclamation facilities, and protect the receiving water bodies. However, developing such control strategies requires significant human and computational resources, and a methodology does not yet exist for quantifying the risks associated with implementing these control strategies. To address these challenges, in this paper, we introduce a Bayesian Optimization-based approach for identifying stormwater control strategies and estimating the associated uncertainties. We evaluate the efficacy of this approach in identifying viable control strategies in a simulated environment on real-world inspired combined and separated stormwater networks. We demonstrate the computational efficiency of the proposed approach by comparing it against a Genetic algorithm. Furthermore, we extend the Bayesian Optimization-based approach to quantify the uncertainty associated with the identified control strategies and evaluate it on a synthetic stormwater network. To our knowledge, this is the first-ever stormwater control methodology that quantifies uncertainty associated with the identified control actions. This Bayesian optimization-based stormwater control methodology is an off-the-shelf control approach that can be applied to control any stormwater network as long we have access to the rainfall predictions, and there exists a model for simulating the behavior of the stormwater network.

Distance-Penalized Active Learning Using Quantile Search

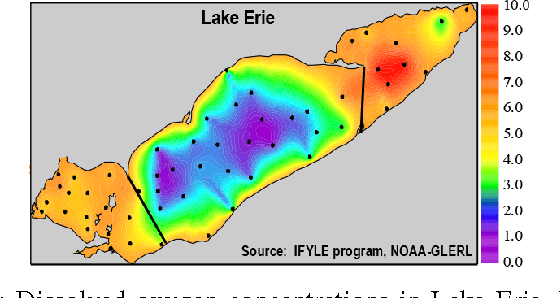
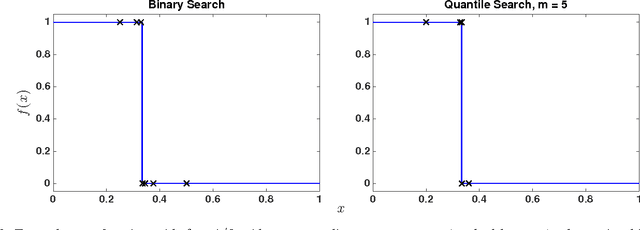
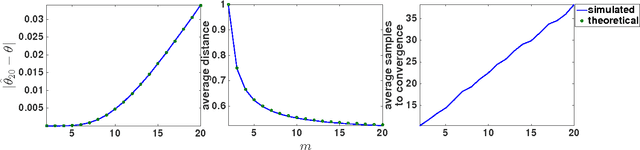
Adaptive sampling theory has shown that, with proper assumptions on the signal class, algorithms exist to reconstruct a signal in $\mathbb{R}^{d}$ with an optimal number of samples. We generalize this problem to the case of spatial signals, where the sampling cost is a function of both the number of samples taken and the distance traveled during estimation. This is motivated by our work studying regions of low oxygen concentration in the Great Lakes. We show that for one-dimensional threshold classifiers, a tradeoff between the number of samples taken and distance traveled can be achieved using a generalization of binary search, which we refer to as quantile search. We characterize both the estimation error after a fixed number of samples and the distance traveled in the noiseless case, as well as the estimation error in the case of noisy measurements. We illustrate our results in both simulations and experiments and show that our method outperforms existing algorithms in the majority of practical scenarios.