Streaming Probabilistic PCA for Missing Data with Heteroscedastic Noise

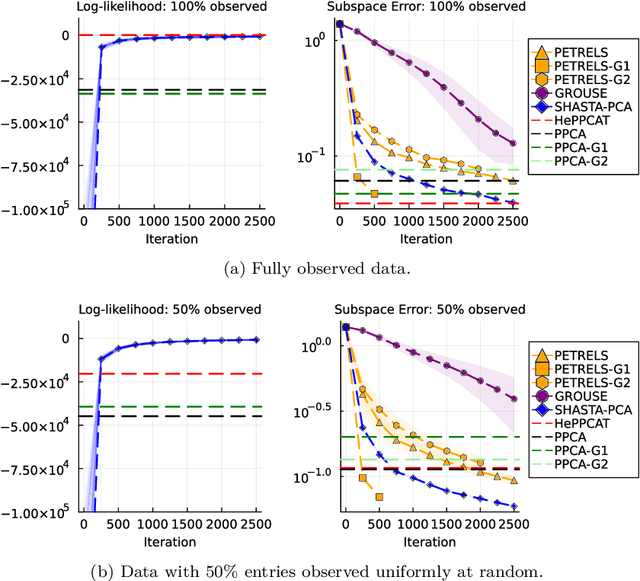
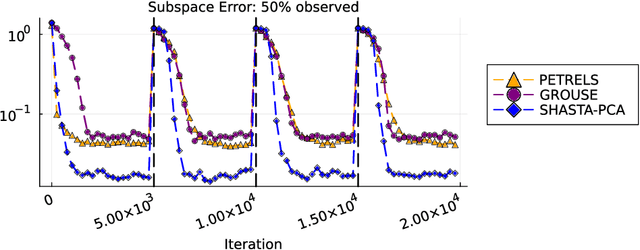
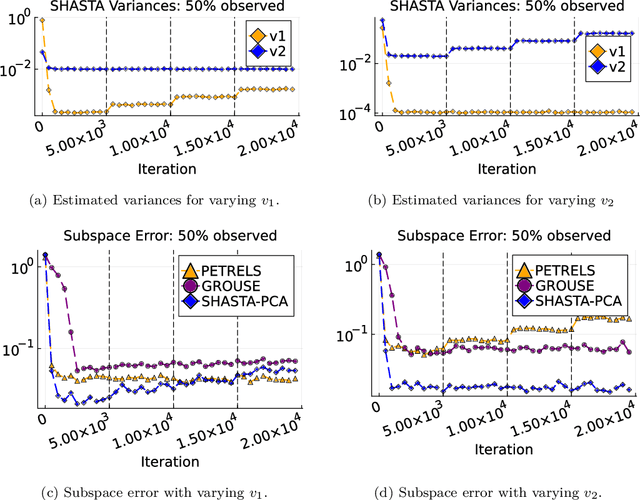
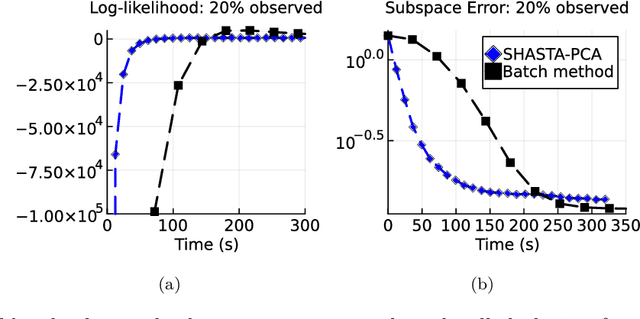
Streaming principal component analysis (PCA) is an integral tool in large-scale machine learning for rapidly estimating low-dimensional subspaces of very high dimensional and high arrival-rate data with missing entries and corrupting noise. However, modern trends increasingly combine data from a variety of sources, meaning they may exhibit heterogeneous quality across samples. Since standard streaming PCA algorithms do not account for non-uniform noise, their subspace estimates can quickly degrade. On the other hand, the recently proposed Heteroscedastic Probabilistic PCA Technique (HePPCAT) addresses this heterogeneity, but it was not designed to handle missing entries and streaming data, nor does it adapt to non-stationary behavior in time series data. This paper proposes the Streaming HeteroscedASTic Algorithm for PCA (SHASTA-PCA) to bridge this divide. SHASTA-PCA employs a stochastic alternating expectation maximization approach that jointly learns the low-rank latent factors and the unknown noise variances from streaming data that may have missing entries and heteroscedastic noise, all while maintaining a low memory and computational footprint. Numerical experiments validate the superior subspace estimation of our method compared to state-of-the-art streaming PCA algorithms in the heteroscedastic setting. Finally, we illustrate SHASTA-PCA applied to highly-heterogeneous real data from astronomy.

HePPCAT: Probabilistic PCA for Data with Heteroscedastic Noise

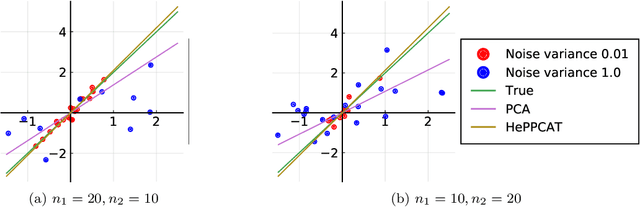
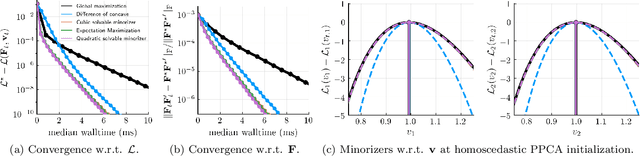
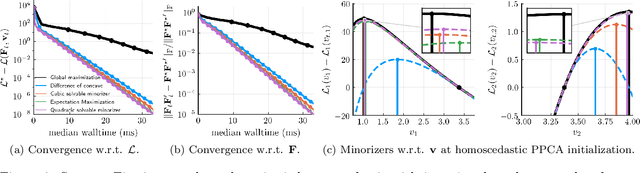
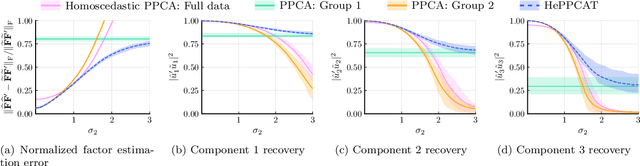
Principal component analysis (PCA) is a classical and ubiquitous method for reducing data dimensionality, but it is suboptimal for heterogeneous data that are increasingly common in modern applications. PCA treats all samples uniformly so degrades when the noise is heteroscedastic across samples, as occurs, e.g., when samples come from sources of heterogeneous quality. This paper develops a probabilistic PCA variant that estimates and accounts for this heterogeneity by incorporating it in the statistical model. Unlike in the homoscedastic setting, the resulting nonconvex optimization problem is not seemingly solved by singular value decomposition. This paper develops a heteroscedastic probabilistic PCA technique (HePPCAT) that uses efficient alternating maximization algorithms to jointly estimate both the underlying factors and the unknown noise variances. Simulation experiments illustrate the comparative speed of the algorithms, the benefit of accounting for heteroscedasticity, and the seemingly favorable optimization landscape of this problem.

Provable tradeoffs in adversarially robust classification

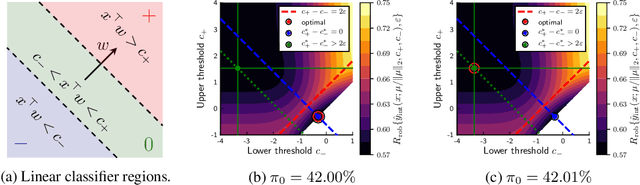
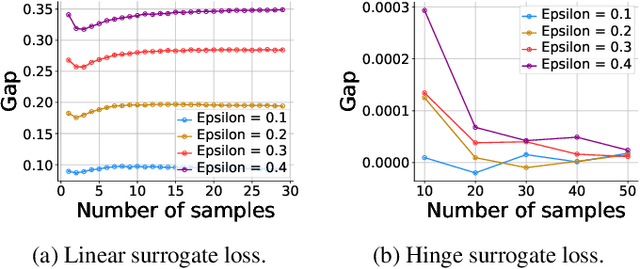
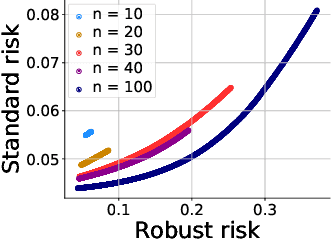
Machine learning methods can be vulnerable to small, adversarially-chosen perturbations of their inputs, prompting much research into theoretical explanations and algorithms toward improving adversarial robustness. Although a rich and insightful literature has developed around these ideas, many foundational open problems remain. In this paper, we seek to address several of these questions by deriving optimal robust classifiers for two- and three-class Gaussian classification problems with respect to adversaries in both the $\ell_2$ and $\ell_\infty$ norms. While the standard non-robust version of this problem has a long history, the corresponding robust setting contains many unexplored problems, and indeed deriving optimal robust classifiers turns out to pose a variety of new challenges. We develop new analysis tools for this task. Our results reveal intriguing tradeoffs between usual and robust accuracy. Furthermore, we give results for data lying on low-dimensional manifolds and study the landscape of adversarially robust risk over linear classifiers, including proving Fisher consistency in some cases. Lastly, we provide novel results concerning finite sample adversarial risk in the Gaussian classification setting.

Baseline Estimation of Commercial Building HVAC Fan Power Using Tensor Completion

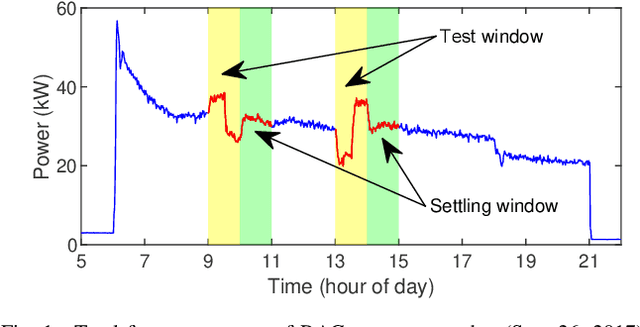
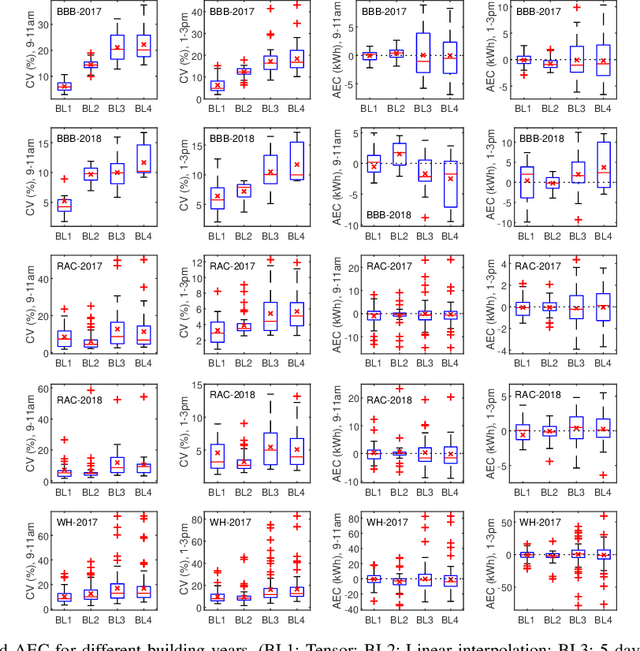
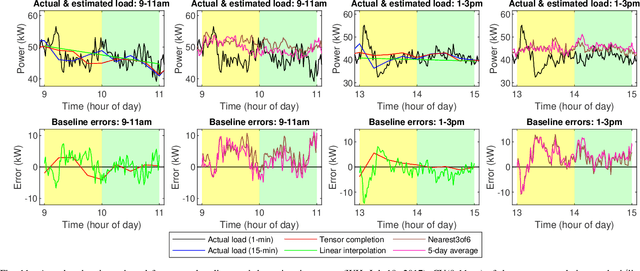
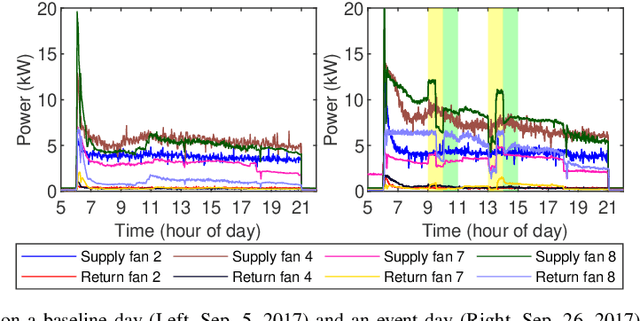
Commercial building heating, ventilation, and air conditioning (HVAC) systems have been studied for providing ancillary services to power grids via demand response (DR). One critical issue is to estimate the counterfactual baseline power consumption that would have prevailed without DR. Baseline methods have been developed based on whole building electric load profiles. New methods are necessary to estimate the baseline power consumption of HVAC sub-components (e.g., supply and return fans), which have different characteristics compared to that of the whole building. Tensor completion can estimate the unobserved entries of multi-dimensional tensors describing complex data sets. It exploits high-dimensional data to capture granular insights into the problem. This paper proposes to use it for baselining HVAC fan power, by utilizing its capability of capturing dominant fan power patterns. The tensor completion method is evaluated using HVAC fan power data from several buildings at the University of Michigan, and compared with several existing methods. The tensor completion method generally outperforms the benchmarks.

Stochastic Gradients for Large-Scale Tensor Decomposition

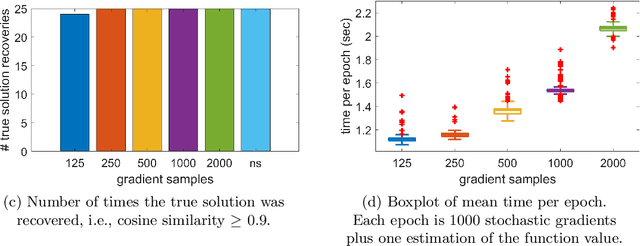
Tensor decomposition is a well-known tool for multiway data analysis. This work proposes using stochastic gradients for efficient generalized canonical polyadic (GCP) tensor decomposition of large-scale tensors. GCP tensor decomposition is a recently proposed version of tensor decomposition that allows for a variety of loss functions such as logistic loss for binary data or Huber loss for robust estimation. The stochastic gradient is formed from randomly sampled elements of the tensor. For dense tensors, we simply use uniform sampling. For sparse tensors, we propose two types of stratified sampling that give precedence to sampling nonzeros. Numerical results demonstrate the advantages of the proposed approach and its scalability to large-scale problems.

Convolutional Analysis Operator Learning: Dependence on Training Data

Convolutional analysis operator learning (CAOL) enables the unsupervised training of (hierachical) convolutional sparsifying operators or autoencoders from large datasets. One can use many training images for CAOL, but a precise understanding of the impact of doing so has remained an open question. This paper presents a series of results that lend insight into the impact of dataset size on the filter update in CAOL. The first result is a general deterministic bound on errors in the estimated filters that then leads to two specific bounds under particular random models. The first bound illustrates a decrease in the expected filter estimation error as the number of training samples increases, and the second bound provides high probability analogues. The bounds depend on properties of the training data, and we investigate their empirical values with real data. Taken together, these results provide evidence for the potential benefit of using more training data in CAOL.

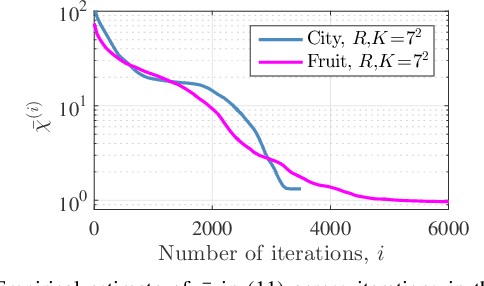
Subspace Clustering using Ensembles of $K$-Subspaces

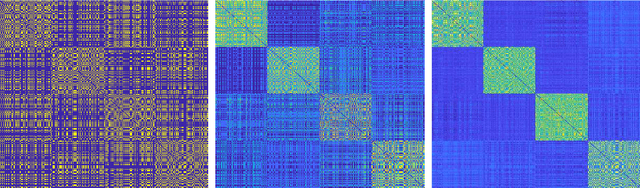
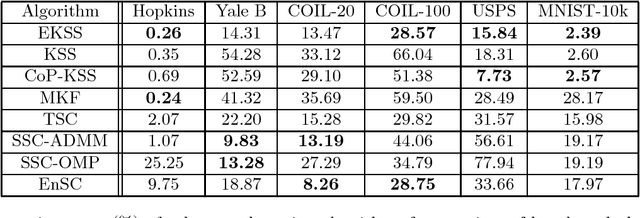
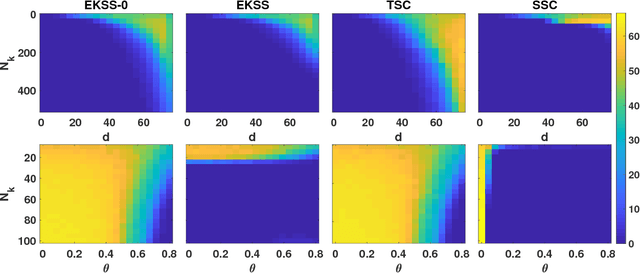
Subspace clustering is the unsupervised grouping of points lying near a union of low-dimensional linear subspaces. Algorithms based directly on geometric properties of such data tend to either provide poor empirical performance, lack theoretical guarantees, or depend heavily on their initialization. We present a novel geometric approach to the subspace clustering problem that leverages ensembles of the K-subspaces (KSS) algorithm via the evidence accumulation clustering framework. Our algorithm, referred to as ensemble K-subspaces (EKSS), forms a co-association matrix whose (i,j)th entry is the number of times points i and j are clustered together by several runs of KSS with random initializations. We prove general recovery guarantees for any algorithm that forms an affinity matrix with entries close to a monotonic transformation of pairwise absolute inner products. We then show that a specific instance of EKSS results in an affinity matrix with entries of this form, and hence our proposed algorithm can provably recover subspaces under similar conditions to state-of-the-art algorithms. The finding is, to the best of our knowledge, the first recovery guarantee for evidence accumulation clustering and for KSS variants. We show on synthetic data that our method performs well in the traditionally challenging settings of subspaces with large intersection, subspaces with small principal angles, and noisy data. Finally, we evaluate our algorithm on six common benchmark datasets and show that unlike existing methods, EKSS achieves excellent empirical performance when there are both a small and large number of points per subspace.

Generalized Canonical Polyadic Tensor Decomposition

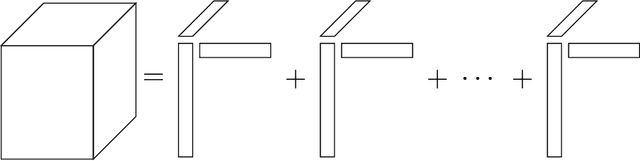
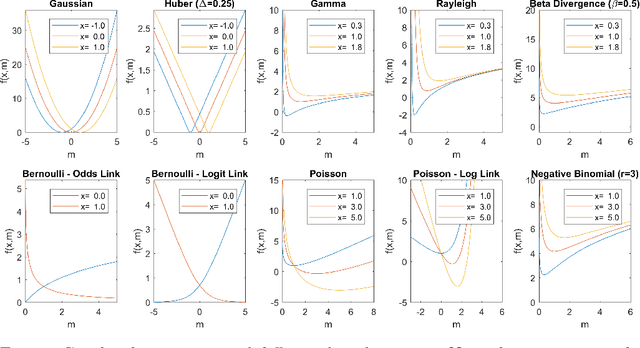
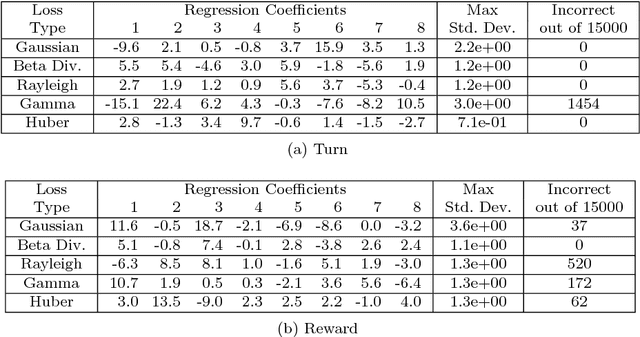
Tensor decomposition is a fundamental unsupervised machine learning method in data science, with applications including network analysis and sensor data processing. This work develops a generalized canonical polyadic (GCP) low-rank tensor decomposition that allows other loss functions besides squared error. For instance, we can use logistic loss or Kullback-Leibler divergence, enabling tensor decomposition for binary or count data. We present a variety statistically-motivated loss functions for various scenarios. We provide a generalized framework for computing gradients and handling missing data that enables the use of standard optimization methods for fitting the model. We demonstrate the flexibility of GCP on several real-world examples including interactions in a social network, neural activity in a mouse, and monthly rainfall measurements in India.

Towards a Theoretical Analysis of PCA for Heteroscedastic Data

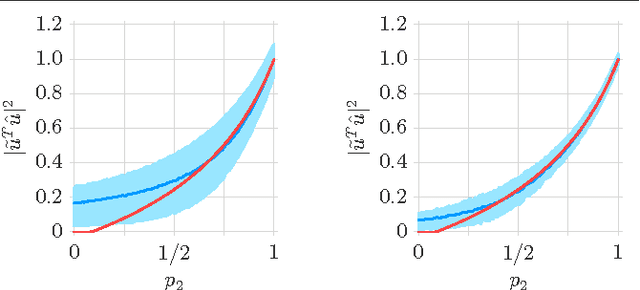
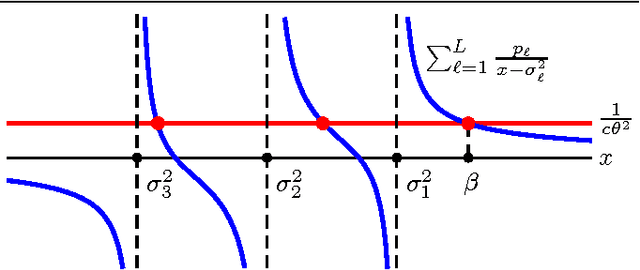
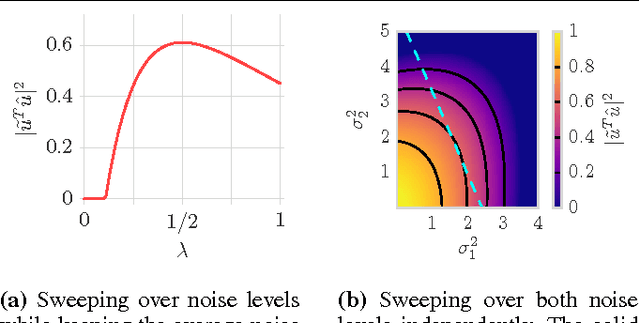
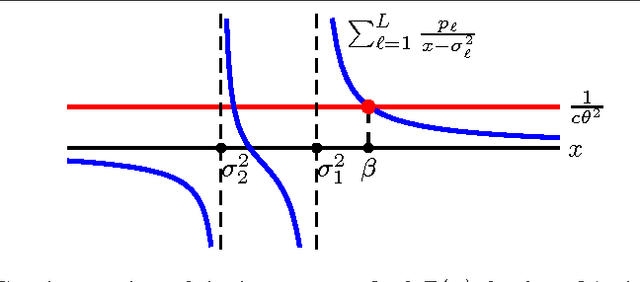
Principal Component Analysis (PCA) is a method for estimating a subspace given noisy samples. It is useful in a variety of problems ranging from dimensionality reduction to anomaly detection and the visualization of high dimensional data. PCA performs well in the presence of moderate noise and even with missing data, but is also sensitive to outliers. PCA is also known to have a phase transition when noise is independent and identically distributed; recovery of the subspace sharply declines at a threshold noise variance. Effective use of PCA requires a rigorous understanding of these behaviors. This paper provides a step towards an analysis of PCA for samples with heteroscedastic noise, that is, samples that have non-uniform noise variances and so are no longer identically distributed. In particular, we provide a simple asymptotic prediction of the recovery of a one-dimensional subspace from noisy heteroscedastic samples. The prediction enables: a) easy and efficient calculation of the asymptotic performance, and b) qualitative reasoning to understand how PCA is impacted by heteroscedasticity (such as outliers).