Provable tradeoffs in adversarially robust classification

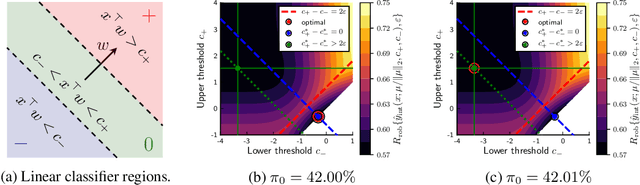
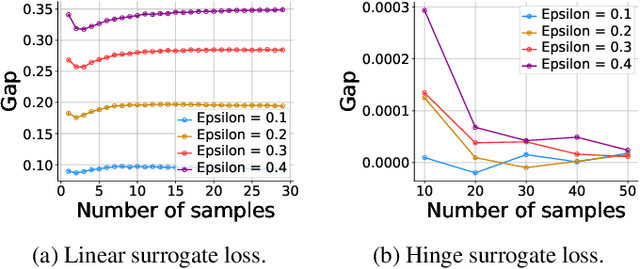
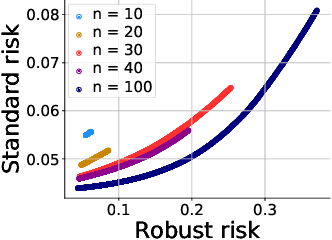
Machine learning methods can be vulnerable to small, adversarially-chosen perturbations of their inputs, prompting much research into theoretical explanations and algorithms toward improving adversarial robustness. Although a rich and insightful literature has developed around these ideas, many foundational open problems remain. In this paper, we seek to address several of these questions by deriving optimal robust classifiers for two- and three-class Gaussian classification problems with respect to adversaries in both the $\ell_2$ and $\ell_\infty$ norms. While the standard non-robust version of this problem has a long history, the corresponding robust setting contains many unexplored problems, and indeed deriving optimal robust classifiers turns out to pose a variety of new challenges. We develop new analysis tools for this task. Our results reveal intriguing tradeoffs between usual and robust accuracy. Furthermore, we give results for data lying on low-dimensional manifolds and study the landscape of adversarially robust risk over linear classifiers, including proving Fisher consistency in some cases. Lastly, we provide novel results concerning finite sample adversarial risk in the Gaussian classification setting.