Streaming Probabilistic PCA for Missing Data with Heteroscedastic Noise

Streaming principal component analysis (PCA) is an integral tool in large-scale machine learning for rapidly estimating low-dimensional subspaces of very high dimensional and high arrival-rate data with missing entries and corrupting noise. However, modern trends increasingly combine data from a variety of sources, meaning they may exhibit heterogeneous quality across samples. Since standard streaming PCA algorithms do not account for non-uniform noise, their subspace estimates can quickly degrade. On the other hand, the recently proposed Heteroscedastic Probabilistic PCA Technique (HePPCAT) addresses this heterogeneity, but it was not designed to handle missing entries and streaming data, nor does it adapt to non-stationary behavior in time series data. This paper proposes the Streaming HeteroscedASTic Algorithm for PCA (SHASTA-PCA) to bridge this divide. SHASTA-PCA employs a stochastic alternating expectation maximization approach that jointly learns the low-rank latent factors and the unknown noise variances from streaming data that may have missing entries and heteroscedastic noise, all while maintaining a low memory and computational footprint. Numerical experiments validate the superior subspace estimation of our method compared to state-of-the-art streaming PCA algorithms in the heteroscedastic setting. Finally, we illustrate SHASTA-PCA applied to highly-heterogeneous real data from astronomy.

A Semidefinite Relaxation for Sums of Heterogeneous Quadratics on the Stiefel Manifold

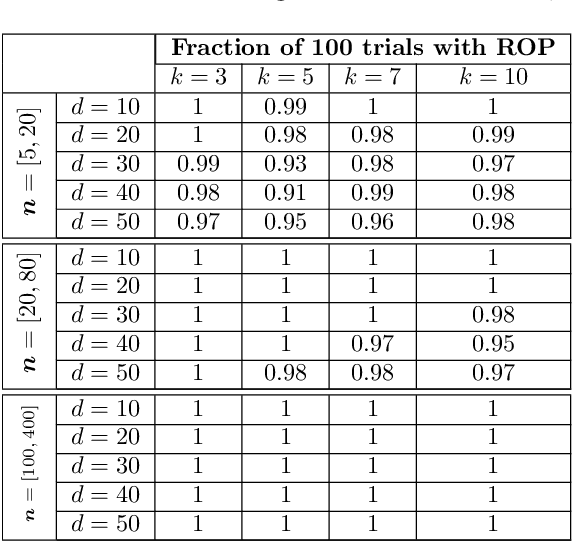
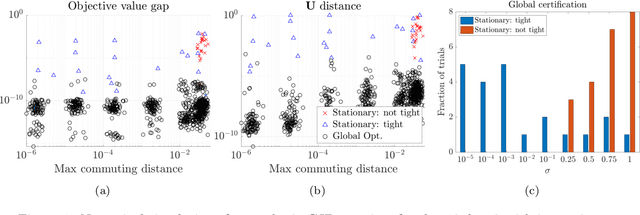
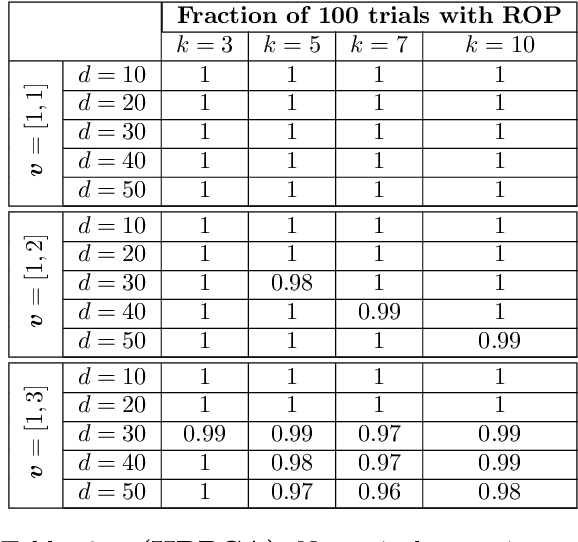
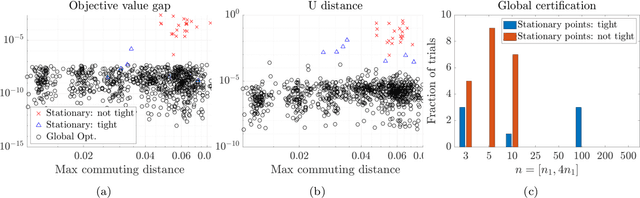
We study the maximization of sums of heterogeneous quadratic functions over the Stiefel manifold, a nonconvex problem that arises in several modern signal processing and machine learning applications such as heteroscedastic probabilistic principal component analysis (HPPCA). In this work, we derive a novel semidefinite program (SDP) relaxation and study a few of its theoretical properties. We prove a global optimality certificate for the original nonconvex problem via a dual certificate, which leads us to propose a simple feasibility problem to certify global optimality of a candidate local solution on the Stiefel manifold. In addition, our relaxation reduces to an assignment linear program for jointly diagonalizable problems and is therefore known to be tight in that case. We generalize this result to show that it is also tight for close-to jointly diagonalizable problems, and we show that the HPPCA problem has this characteristic. Numerical results validate our global optimality certificate and sufficient conditions for when the SDP is tight in various problem settings.

HePPCAT: Probabilistic PCA for Data with Heteroscedastic Noise

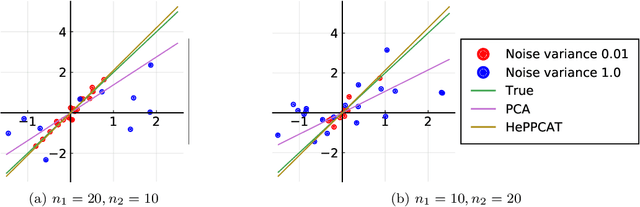
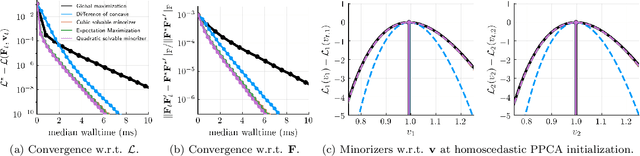
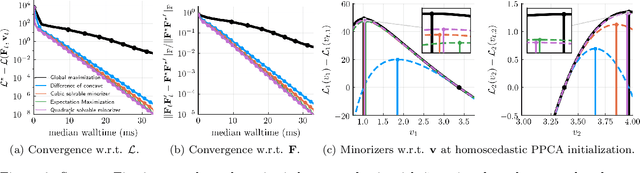
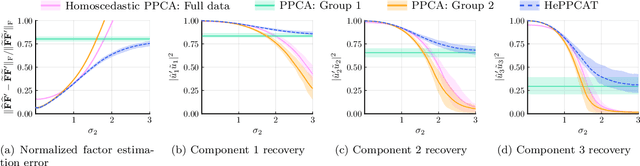
Principal component analysis (PCA) is a classical and ubiquitous method for reducing data dimensionality, but it is suboptimal for heterogeneous data that are increasingly common in modern applications. PCA treats all samples uniformly so degrades when the noise is heteroscedastic across samples, as occurs, e.g., when samples come from sources of heterogeneous quality. This paper develops a probabilistic PCA variant that estimates and accounts for this heterogeneity by incorporating it in the statistical model. Unlike in the homoscedastic setting, the resulting nonconvex optimization problem is not seemingly solved by singular value decomposition. This paper develops a heteroscedastic probabilistic PCA technique (HePPCAT) that uses efficient alternating maximization algorithms to jointly estimate both the underlying factors and the unknown noise variances. Simulation experiments illustrate the comparative speed of the algorithms, the benefit of accounting for heteroscedasticity, and the seemingly favorable optimization landscape of this problem.

Grassmannian Optimization for Online Tensor Completion and Tracking in the t-SVD Algebra

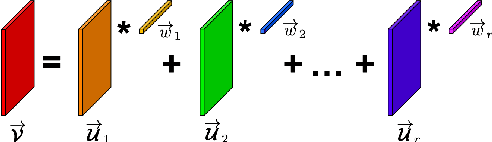
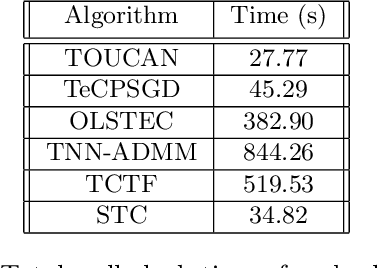
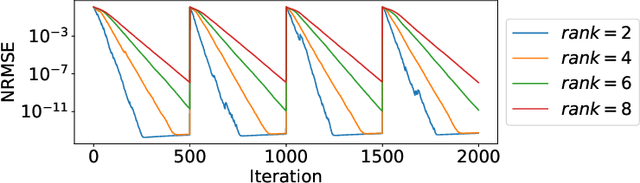
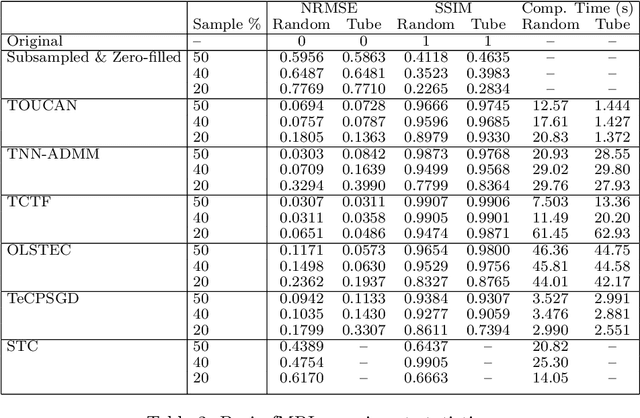
We propose a new streaming algorithm, called TOUCAN, for the tensor completion problem of imputing missing entries of a low-tubal-rank tensor using the recently proposed tensor-tensor product (t-product) and tensor singular value decomposition (t-SVD) algebraic framework. We also demonstrate TOUCAN's ability to track changing free submodules from highly incomplete streaming 2-D data. TOUCAN uses principles from incremental gradient descent on the Grassmann manifold of subspaces to solve the tensor completion problem with linear complexity and constant memory in the number of time samples. We compare our results to state-of-the-art tensor completion algorithms in real applications to recover temporal chemo-sensing data and MRI data under limited sampling.