A Semidefinite Relaxation for Sums of Heterogeneous Quadratics on the Stiefel Manifold
Paper and Code
May 26, 2022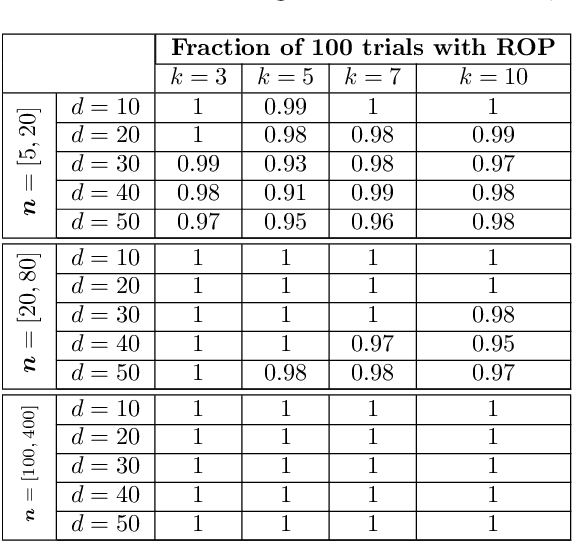
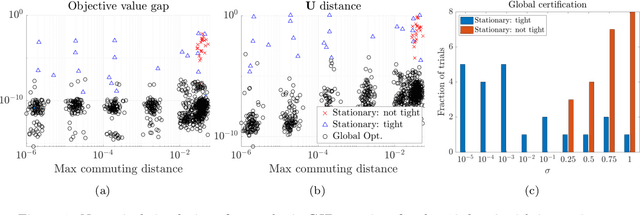
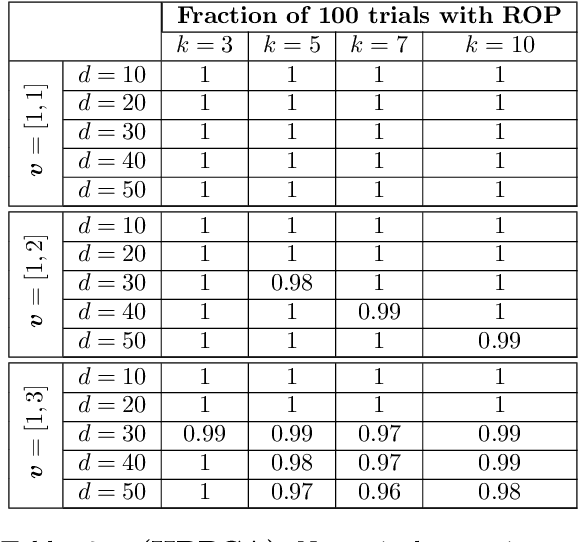
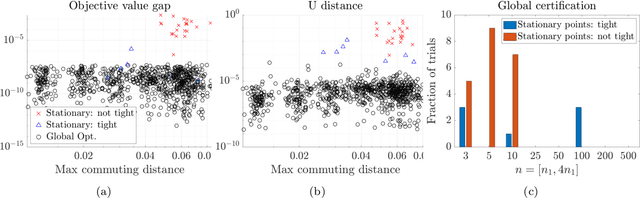
We study the maximization of sums of heterogeneous quadratic functions over the Stiefel manifold, a nonconvex problem that arises in several modern signal processing and machine learning applications such as heteroscedastic probabilistic principal component analysis (HPPCA). In this work, we derive a novel semidefinite program (SDP) relaxation and study a few of its theoretical properties. We prove a global optimality certificate for the original nonconvex problem via a dual certificate, which leads us to propose a simple feasibility problem to certify global optimality of a candidate local solution on the Stiefel manifold. In addition, our relaxation reduces to an assignment linear program for jointly diagonalizable problems and is therefore known to be tight in that case. We generalize this result to show that it is also tight for close-to jointly diagonalizable problems, and we show that the HPPCA problem has this characteristic. Numerical results validate our global optimality certificate and sufficient conditions for when the SDP is tight in various problem settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge