Brian D. O. Anderson
Neighboring Extremal Optimal Control Theory for Parameter-Dependent Closed-loop Laws
Dec 07, 2023Abstract:This study introduces an approach to obtain a neighboring extremal optimal control (NEOC) solution for a closed-loop optimal control problem, applicable to a wide array of nonlinear systems and not necessarily quadratic performance indices. The approach involves investigating the variation incurred in the functional form of a known closed-loop optimal control law due to small, known parameter variations in the system equations or the performance index. The NEOC solution can formally be obtained by solving a linear partial differential equation, akin to those encountered in the iterative solution of a nonlinear Hamilton-Jacobi equation. Motivated by numerical procedures for solving these latter equations, we also propose a numerical algorithm based on the Galerkin algorithm, leveraging the use of basis functions to solve the underlying Hamilton-Jacobi equation of the original optimal control problem. The proposed approach simplifies the NEOC problem by reducing it to the solution of a simple set of linear equations, thereby eliminating the need for a full re-solution of the adjusted optimal control problem. Furthermore, the variation to the optimal performance index can be obtained as a function of both the system state and small changes in parameters, allowing the determination of the adjustment to an optimal control law given a small adjustment of parameters in the system or the performance index. Moreover, in order to handle large known parameter perturbations, we propose a homotopic approach that breaks down the single calculation of NEOC into a finite set of multiple steps. Finally, the validity of the claims and theory is supported by theoretical analysis and numerical simulations.
Cooperative constrained motion coordination of networked heterogeneous vehicles
Jan 17, 2022Abstract:We consider the problem of cooperative motion coordination for multiple heterogeneous mobile vehicles subject to various constraints. These include nonholonomic motion constraints, constant speed constraints, holonomic coordination constraints, and equality/inequality geometric constraints. We develop a general framework involving differential-algebraic equations and viability theory to determine coordination feasibility for a coordinated motion control under heterogeneous vehicle dynamics and different types of coordination task constraints. If a coordinated motion solution exists for the derived differential-algebraic equations and/or inequalities, a constructive algorithm is proposed to derive an equivalent dynamical system that generates a set of feasible coordinated motions for each individual vehicle. In case studies on coordinating two vehicles, we derive analytical solutions to motion generation for two-vehicle groups consisting of car-like vehicles, unicycle vehicles, or vehicles with constant speeds, which serve as benchmark coordination tasks for more complex vehicle groups. The motion generation algorithm is well-backed by simulation data for a wide variety of coordination situations involving heterogeneous vehicles. We then extend the vehicle control framework to deal with the cooperative coordination problem with time-varying coordination tasks and leader-follower structure. We show several simulation experiments on multi-vehicle coordination under various constraints to validate the theory and the effectiveness of the proposed schemes.
Cooperative event-based rigid formation control
Jan 11, 2019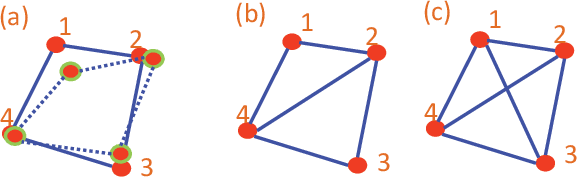
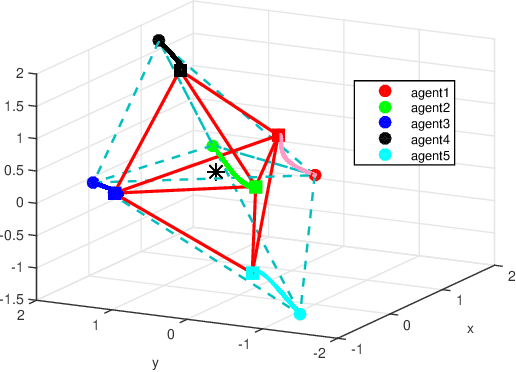
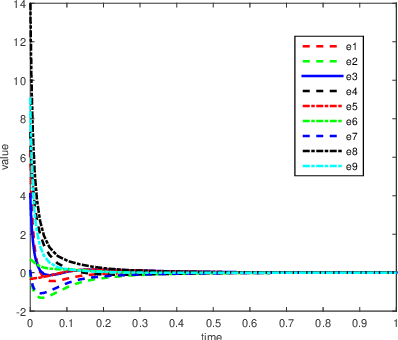
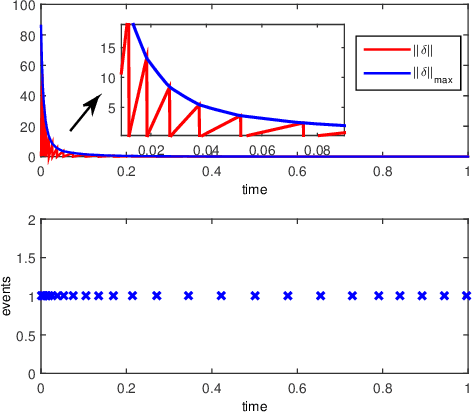
Abstract:This paper discusses cooperative stabilization control of rigid formations via an event-based approach. We first design a centralized event-based formation control system, in which a central event controller determines the next triggering time and broadcasts the event signal to all the agents for control input update. We then build on this approach to propose a distributed event control strategy, in which each agent can use its local event trigger and local information to update the control input at its own event time. For both cases, the triggering condition, event function and triggering behavior are discussed in detail, and the exponential convergence of the event-based formation system is guaranteed.
Cooperative Localisation of a GPS-Denied UAV using Direction of Arrival Measurements
Nov 20, 2018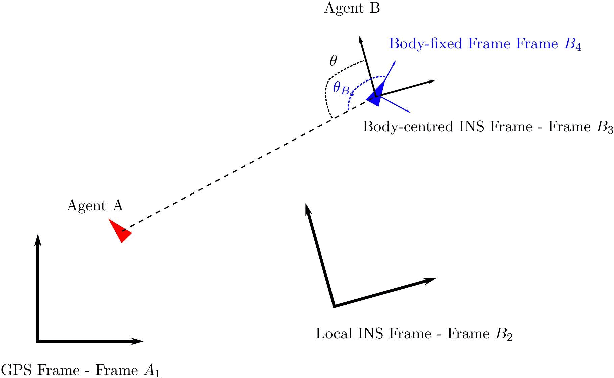
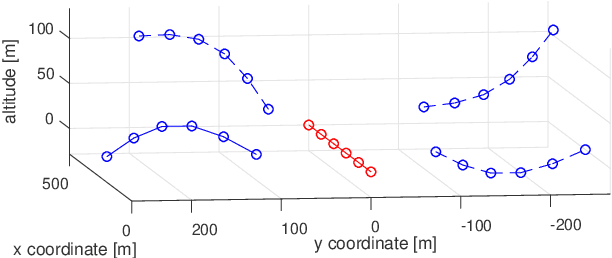
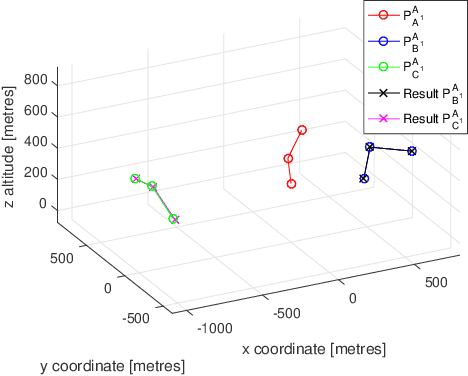
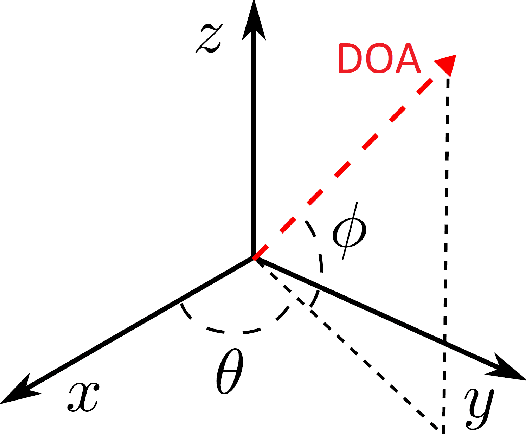
Abstract:A GPS-denied UAV (Agent B) is localised through INS alignment with the aid of a nearby GPS-equipped UAV (Agent A), which broadcasts its position at several time instants. Agent B measures the signals' direction of arrival with respect to Agent B's inertial navigation frame. Semidefinite programming and the Orthogonal Procrustes algorithm are employed, and accuracy is improved through maximum likelihood estimation. The method is validated using flight data and simulations. A three-agent extension is explored.
Collaborative target-tracking control using multiple autonomous fixed-wing UAVs with constant speeds: Theory and experiments
Sep 29, 2018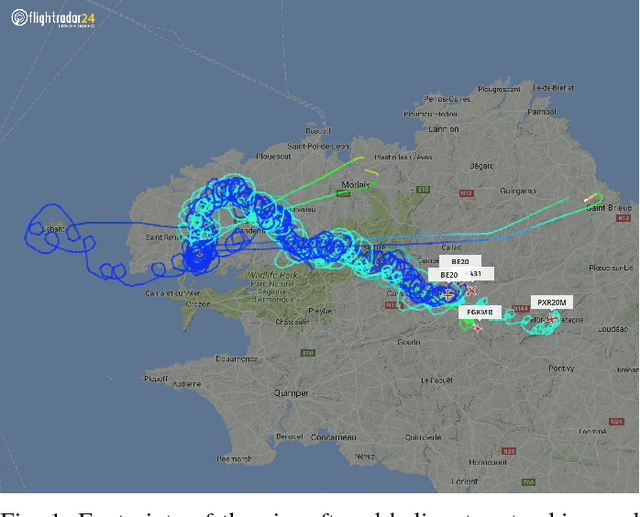


Abstract:This paper considers a collaborative tracking control problem using a group of fixed-wing UAVs with constant and non-identical speeds. The dynamics of fixed-wing UAVs are modelled by unicycle-type equations, with nonholonomic constraints by assuming that UAVs fly at constant attitudes in the nominal operation mode. The control focus is on the design of a collective tracking controller such that all fixed-wing UAVs as a group can collaboratively track a desired target's position and velocity. We construct a reference velocity that includes both the target's velocity and position as feedback, which is to be tracked by the group centroid. In this way, all vehicles' headings are controlled such that the group centroid follows a reference trajectory that successfully tracks the target's trajectory. We consider three cases of reference velocity tracking: the constant velocity case, the turning velocity case with constant speed, and the time-varying velocity case. An additive spacing controller is further devised to ensure that all vehicles stay close to the group centroid trajectory. Trade-offs and performance limitations of the target tracking control due to the constant-speed constraint are also discussed in detail. Experimental results with three fixed-wing UAVs tracking a target rotorcraft are shown to validate the effectiveness and performance of the proposed tracking controllers.
Controlling a triangular flexible formation of autonomous agents
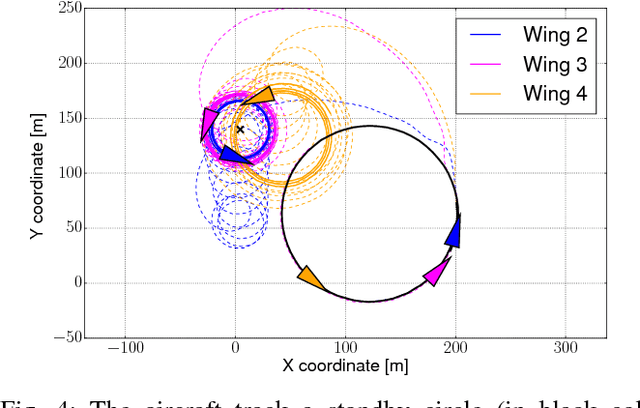
Apr 03, 2017
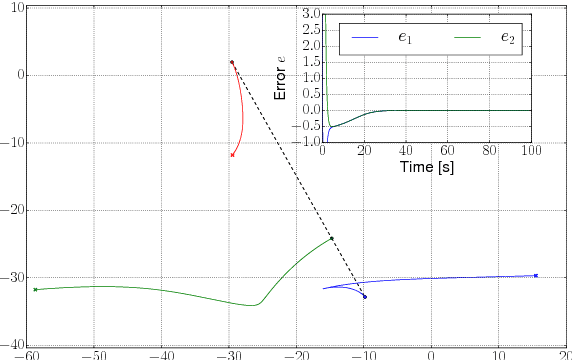
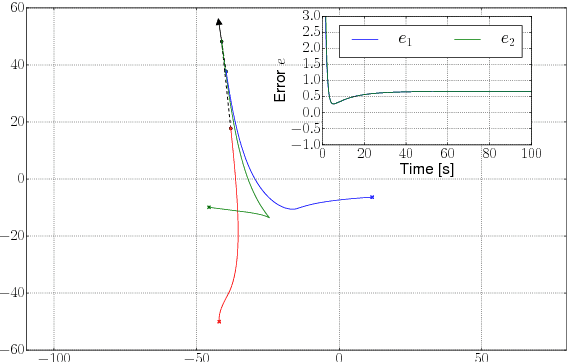
Abstract:In formation control, triangular formations consisting of three autonomous agents serve as a class of benchmarks that can be used to test and compare the performances of different controllers. We present an algorithm that combines the advantages of both position- and distance-based gradient descent control laws. For example, only two pairs of neighboring agents need to be controlled, agents can work in their own local frame of coordinates and the orientation of the formation with respect to a global frame of coordinates is not prescribed. We first present a novel technique based on adding artificial biases to neighboring agents' range sensors such that their eventual positions correspond to a collinear configuration. Right after, a small modification in the bias terms by introducing a prescribed rotation matrix will allow the control of the bearing of the neighboring agents.
Cooperative Localisation of a GPS-Denied UAV in 3-Dimensional Space Using Direction of Arrival Measurements
Mar 18, 2017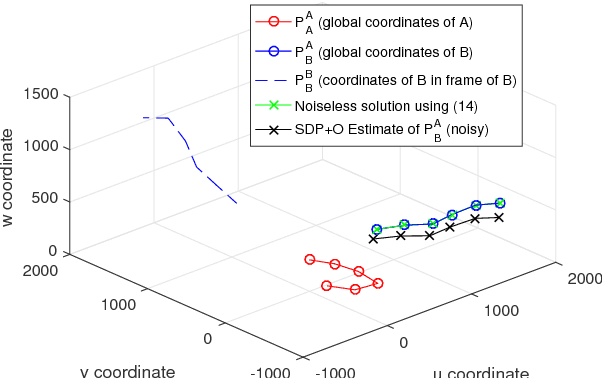
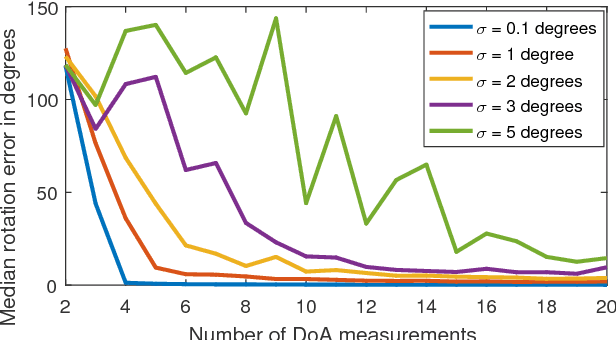
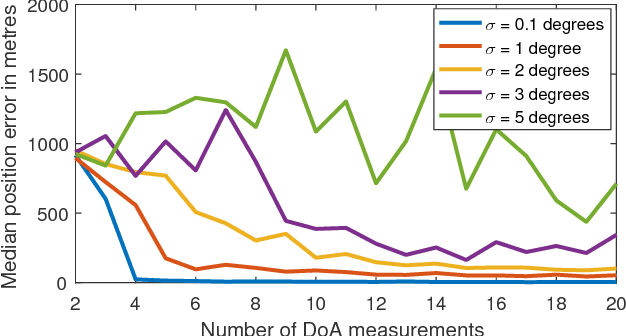
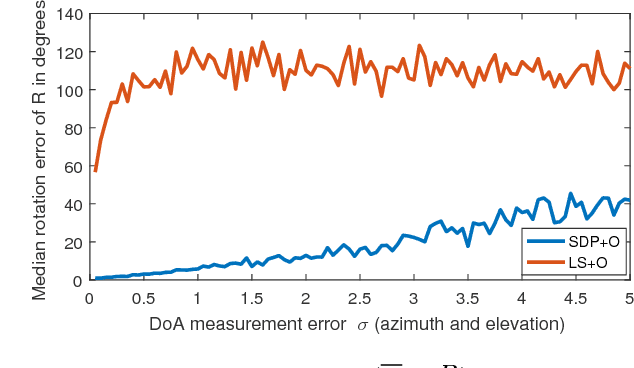
Abstract:This paper presents a novel approach for localising a GPS (Global Positioning System)-denied Unmanned Aerial Vehicle (UAV) with the aid of a GPS-equipped UAV in three-dimensional space. The GPS-equipped UAV makes discrete-time broadcasts of its global coordinates. The GPS-denied UAV simultaneously receives the broadcast and takes direction of arrival (DOA) measurements towards the origin of the broadcast in its local coordinate frame (obtained via an inertial navigation system (INS)). The aim is to determine the difference between the local and global frames, described by a rotation and a translation. In the noiseless case, global coordinates were recovered exactly by solving a system of linear equations. When DOA measurements are contaminated with noise, rank relaxed semidefinite programming (SDP) and the Orthogonal Procrustes algorithm are employed. Simulations are provided and factors affecting accuracy, such as noise levels and number of measurements, are explored.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge