Cooperative constrained motion coordination of networked heterogeneous vehicles

We consider the problem of cooperative motion coordination for multiple heterogeneous mobile vehicles subject to various constraints. These include nonholonomic motion constraints, constant speed constraints, holonomic coordination constraints, and equality/inequality geometric constraints. We develop a general framework involving differential-algebraic equations and viability theory to determine coordination feasibility for a coordinated motion control under heterogeneous vehicle dynamics and different types of coordination task constraints. If a coordinated motion solution exists for the derived differential-algebraic equations and/or inequalities, a constructive algorithm is proposed to derive an equivalent dynamical system that generates a set of feasible coordinated motions for each individual vehicle. In case studies on coordinating two vehicles, we derive analytical solutions to motion generation for two-vehicle groups consisting of car-like vehicles, unicycle vehicles, or vehicles with constant speeds, which serve as benchmark coordination tasks for more complex vehicle groups. The motion generation algorithm is well-backed by simulation data for a wide variety of coordination situations involving heterogeneous vehicles. We then extend the vehicle control framework to deal with the cooperative coordination problem with time-varying coordination tasks and leader-follower structure. We show several simulation experiments on multi-vehicle coordination under various constraints to validate the theory and the effectiveness of the proposed schemes.

Segmentation of Robot Movements using Position and Contact Forces

In this paper, a method for autonomous segmentation of demonstrated robot movements is proposed. Position data is clustered into Gaussian mixture models (GMMs), and an initial set of segments is identified from the Gaussian basis functions. A Kalman filter is used to detect sudden changes in the contact force/torque measurements, and this is used to update and verify the initial segmentation points. The segmentation method is verified experimentally on an industrial robot.

Temporally Coupled Dynamical Movement Primitives in Cartesian Space

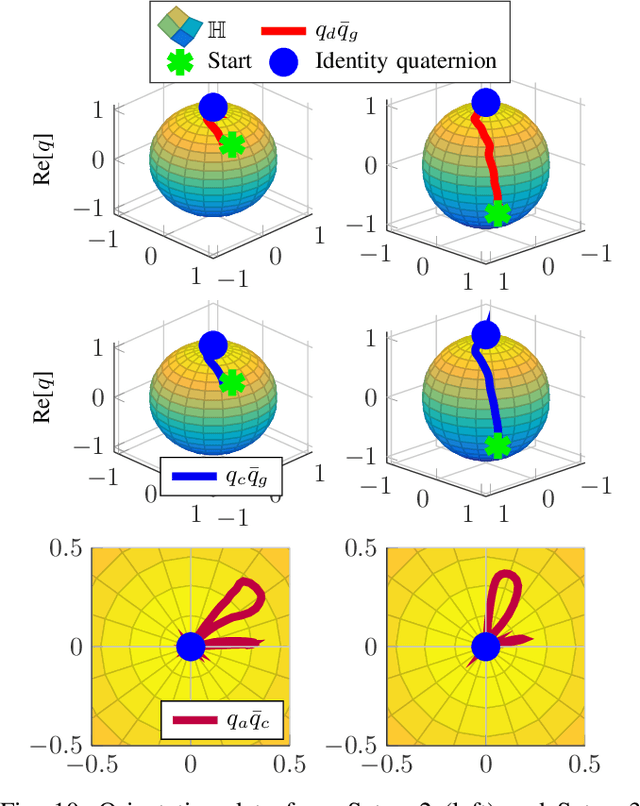
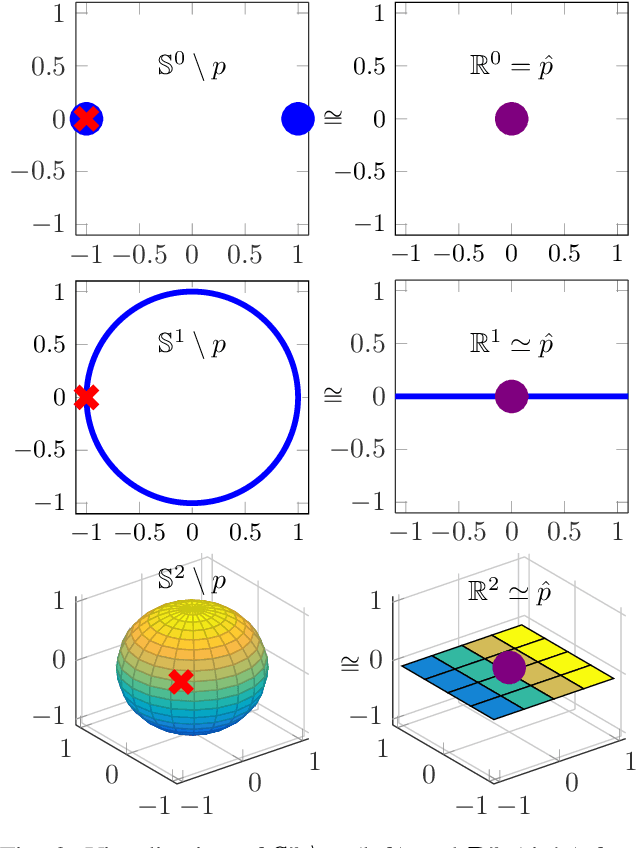
Control of robot orientation in Cartesian space implicates some difficulties, because the rotation group SO(3) is not contractible, and only globally contractible state spaces support continuous and globally asymptotically stable feedback control systems. In this paper, unit quaternions are used to represent orientations, and it is first shown that the unit quaternion set minus one single point is contractible. This is used to design a control system for temporally coupled dynamical movement primitives (DMPs) in Cartesian space. The functionality of the control system is verified experimentally on an industrial robot.

Autonomous Interpretation of Demonstrations for Modification of Dynamical Movement Primitives

The concept of dynamical movement primitives (DMPs) has become popular for modeling of motion, commonly applied to robots. This paper presents a framework that allows a robot operator to adjust DMPs in an intuitive way. Given a generated trajectory with a faulty last part, the operator can use lead-through programming to demonstrate a corrective trajectory. A modified DMP is formed, based on the first part of the faulty trajectory and the last part of the corrective one. A real-time application is presented and verified experimentally.

Temporal viability regulation for control affine systems with applications to mobile vehicle coordination under time-varying motion constraints

Controlled invariant set and viability regulation of dynamical control systems have played important roles in many control and coordination applications. In this paper we develop a temporal viability regulation theory for general dynamical control systems, and in particular for control affine systems. The time-varying viable set is parameterized by time-varying constraint functions, with the aim to regulate a dynamical control system to be invariant in the time-varying viable set so that temporal state-dependent constraints are enforced. We consider both time-varying equality and inequality constraints in defining a temporal viable set. We also present sufficient conditions for the existence of feasible control input for the control affine systems. The developed temporal viability regulation theory is applied to mobile vehicle coordination.

Tangent-Space Regularization for Neural-Network Models of Dynamical Systems

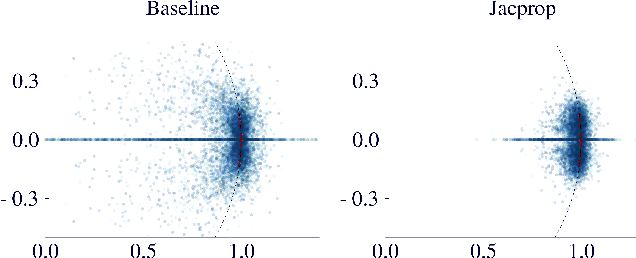
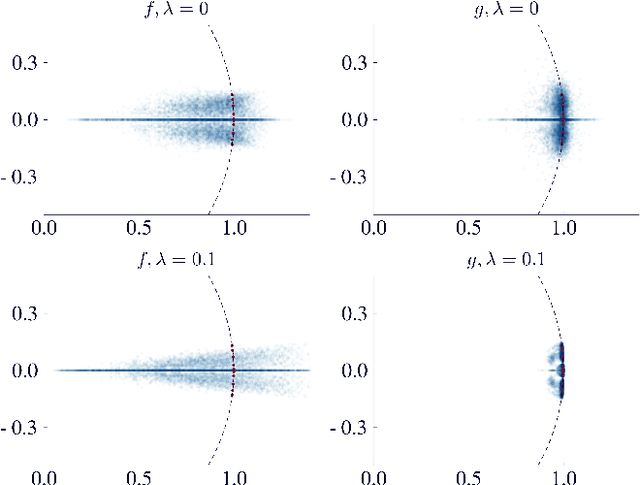
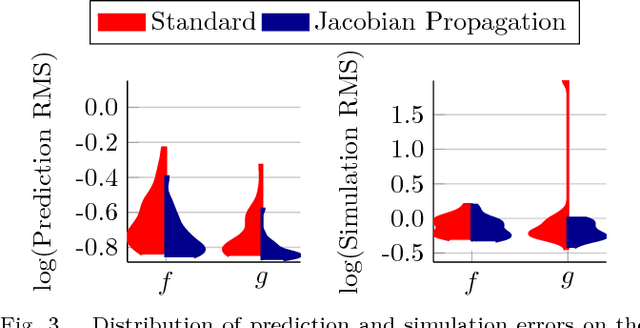
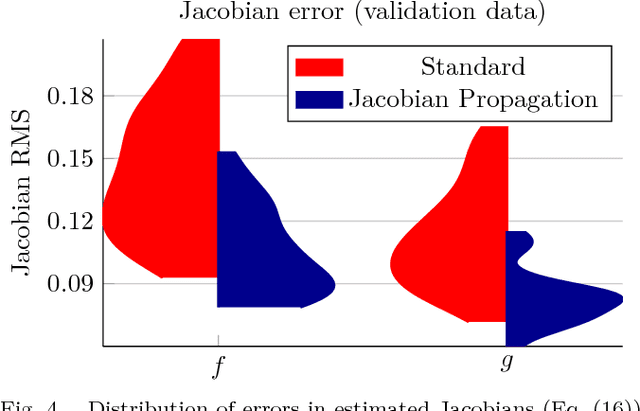
This work introduces the concept of tangent space regularization for neural-network models of dynamical systems. The tangent space to the dynamics function of many physical systems of interest in control applications exhibits useful properties, e.g., smoothness, motivating regularization of the model Jacobian along system trajectories using assumptions on the tangent space of the dynamics. Without assumptions, large amounts of training data are required for a neural network to learn the full non-linear dynamics without overfitting. We compare different network architectures on one-step prediction and simulation performance and investigate the propensity of different architectures to learn models with correct input-output Jacobian. Furthermore, the influence of $L_2$ weight regularization on the learned Jacobian eigenvalue spectrum, and hence system stability, is investigated.

Identification of LTV Dynamical Models with Smooth or Discontinuous Time Evolution by means of Convex Optimization

We establish a connection between trend filtering and system identification which results in a family of new identification methods for linear, time-varying (LTV) dynamical models based on convex optimization. We demonstrate how the design of the cost function promotes a model with either a continuous change in dynamics over time, or causes discontinuous changes in model coefficients occurring at a finite (sparse) set of time instances. We further discuss the introduction of priors on the model parameters for situations where excitation is insufficient for identification. The identification problems are cast as convex optimization problems and are applicable to, e.g., ARX models and state-space models with time-varying parameters. We illustrate usage of the methods in simulations of jump-linear systems, a nonlinear robot arm with non-smooth friction and stiff contacts as well as in model-based, trajectory centric reinforcement learning on a smooth nonlinear system.