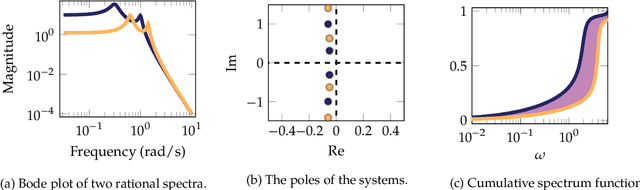
New Metrics Between Rational Spectra and their Connection to Optimal Transport

We propose a series of metrics between pairs of signals, linear systems or rational spectra, based on optimal transport and linear-systems theory. The metrics operate on the locations of the poles of rational functions and admit very efficient computation of distances, barycenters, displacement interpolation and projections. We establish the connection to the Wasserstein distance between rational spectra, and demonstrate the use of the metrics in tasks such as signal classification, clustering, detection and approximation.

Machine Learning and System Identification for Estimation in Physical Systems

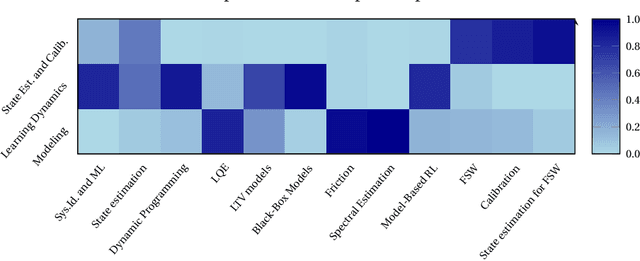
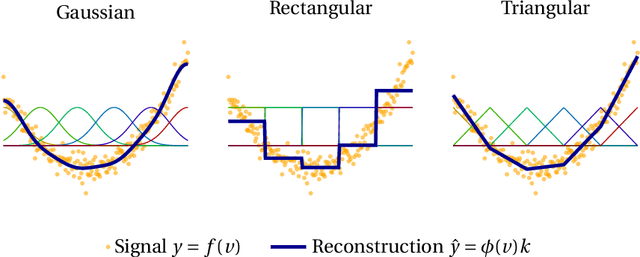
In this thesis, we draw inspiration from both classical system identification and modern machine learning in order to solve estimation problems for real-world, physical systems. The main approach to estimation and learning adopted is optimization based. Concepts such as regularization will be utilized for encoding of prior knowledge and basis-function expansions will be used to add nonlinear modeling power while keeping data requirements practical. The thesis covers a wide range of applications, many inspired by applications within robotics, but also extending outside this already wide field. Usage of the proposed methods and algorithms are in many cases illustrated in the real-world applications that motivated the research. Topics covered include dynamics modeling and estimation, model-based reinforcement learning, spectral estimation, friction modeling and state estimation and calibration in robotic machining. In the work on modeling and identification of dynamics, we develop regularization strategies that allow us to incorporate prior domain knowledge into flexible, overparameterized models. We make use of classical control theory to gain insight into training and regularization while using flexible tools from modern deep learning. A particular focus of the work is to allow use of modern methods in scenarios where gathering data is associated with a high cost. In the robotics-inspired parts of the thesis, we develop methods that are practically motivated and ensure that they are implementable also outside the research setting. We demonstrate this by performing experiments in realistic settings and providing open-source implementations of all proposed methods and algorithms.

On the Calibration of Force/Torque Sensors in Robotics

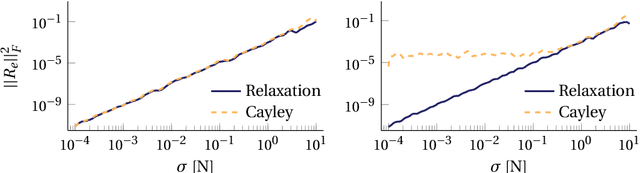
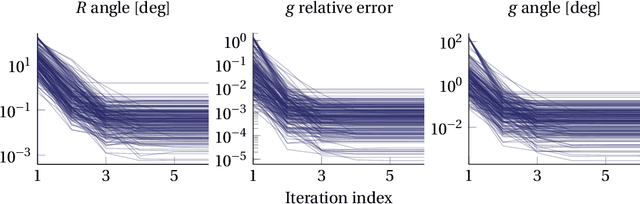
We present and analyze methods for the kinematic and kinetostatic calibration of, typically, wrist mounted force/torque sensors in robotics. The algorithms are based on matrix factorization and require no special equipment. The only requirement is the ability to reorient the sensor and to measure its orientation in a fixed coordinate system, such as through the forward kinematics of a robot manipulator, or using an external tracking system. We present methods to find the rotation matrix between the coordinate system of the sensor and that of the tool flange, the mass held by the force sensor at rest, the vector to the center of gravity of this mass and the gravitational acceleration vector.

Tangent-Space Regularization for Neural-Network Models of Dynamical Systems

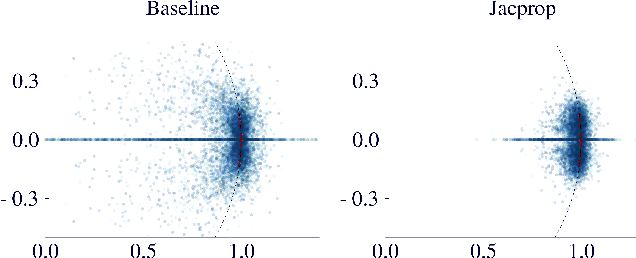
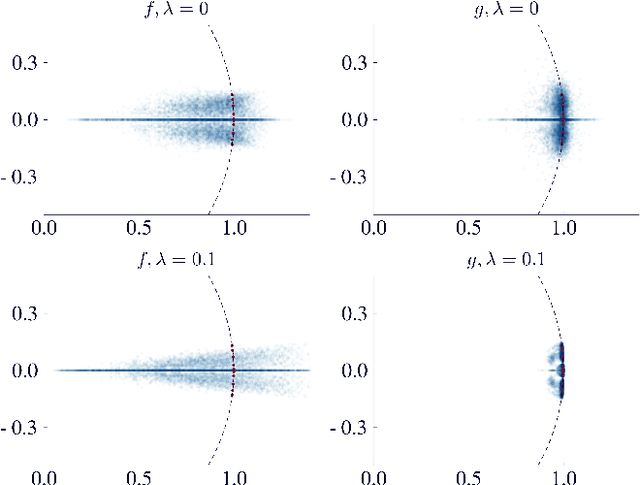
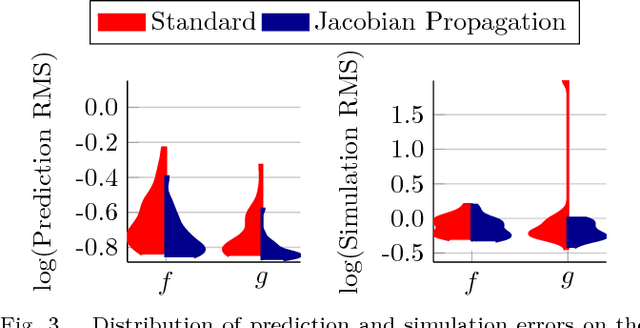
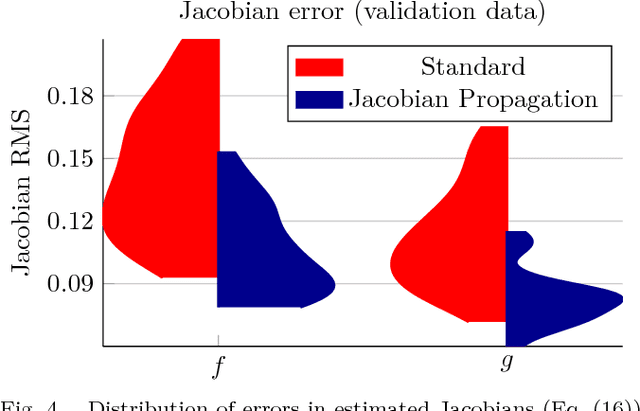
This work introduces the concept of tangent space regularization for neural-network models of dynamical systems. The tangent space to the dynamics function of many physical systems of interest in control applications exhibits useful properties, e.g., smoothness, motivating regularization of the model Jacobian along system trajectories using assumptions on the tangent space of the dynamics. Without assumptions, large amounts of training data are required for a neural network to learn the full non-linear dynamics without overfitting. We compare different network architectures on one-step prediction and simulation performance and investigate the propensity of different architectures to learn models with correct input-output Jacobian. Furthermore, the influence of $L_2$ weight regularization on the learned Jacobian eigenvalue spectrum, and hence system stability, is investigated.

Identification of LTV Dynamical Models with Smooth or Discontinuous Time Evolution by means of Convex Optimization

We establish a connection between trend filtering and system identification which results in a family of new identification methods for linear, time-varying (LTV) dynamical models based on convex optimization. We demonstrate how the design of the cost function promotes a model with either a continuous change in dynamics over time, or causes discontinuous changes in model coefficients occurring at a finite (sparse) set of time instances. We further discuss the introduction of priors on the model parameters for situations where excitation is insufficient for identification. The identification problems are cast as convex optimization problems and are applicable to, e.g., ARX models and state-space models with time-varying parameters. We illustrate usage of the methods in simulations of jump-linear systems, a nonlinear robot arm with non-smooth friction and stiff contacts as well as in model-based, trajectory centric reinforcement learning on a smooth nonlinear system.