New Metrics Between Rational Spectra and their Connection to Optimal Transport
Paper and Code
Apr 20, 2020
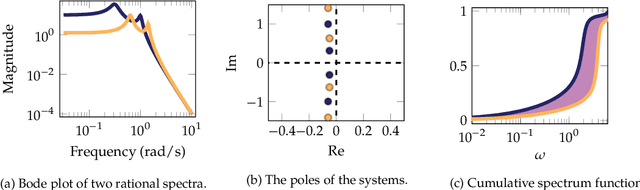


We propose a series of metrics between pairs of signals, linear systems or rational spectra, based on optimal transport and linear-systems theory. The metrics operate on the locations of the poles of rational functions and admit very efficient computation of distances, barycenters, displacement interpolation and projections. We establish the connection to the Wasserstein distance between rational spectra, and demonstrate the use of the metrics in tasks such as signal classification, clustering, detection and approximation.
* 17 pages, 12 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge