Value-based Fast and Slow AI Nudging

Nudging is a behavioral strategy aimed at influencing people's thoughts and actions. Nudging techniques can be found in many situations in our daily lives, and these nudging techniques can targeted at human fast and unconscious thinking, e.g., by using images to generate fear or the more careful and effortful slow thinking, e.g., by releasing information that makes us reflect on our choices. In this paper, we propose and discuss a value-based AI-human collaborative framework where AI systems nudge humans by proposing decision recommendations. Three different nudging modalities, based on when recommendations are presented to the human, are intended to stimulate human fast thinking, slow thinking, or meta-cognition. Values that are relevant to a specific decision scenario are used to decide when and how to use each of these nudging modalities. Examples of values are decision quality, speed, human upskilling and learning, human agency, and privacy. Several values can be present at the same time, and their priorities can vary over time. The framework treats values as parameters to be instantiated in a specific decision environment.

Learning Behavioral Soft Constraints from Demonstrations

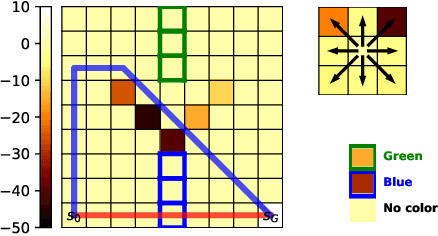
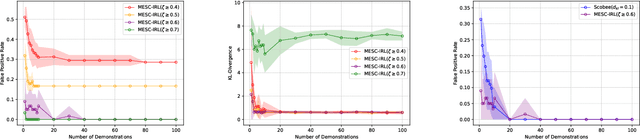
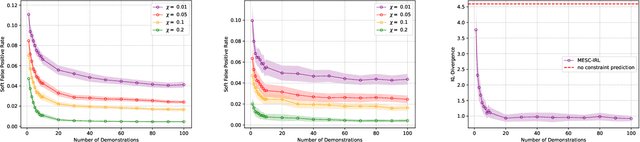
Many real-life scenarios require humans to make difficult trade-offs: do we always follow all the traffic rules or do we violate the speed limit in an emergency? These scenarios force us to evaluate the trade-off between collective rules and norms with our own personal objectives and desires. To create effective AI-human teams, we must equip AI agents with a model of how humans make these trade-offs in complex environments when there are implicit and explicit rules and constraints. Agent equipped with these models will be able to mirror human behavior and/or to draw human attention to situations where decision making could be improved. To this end, we propose a novel inverse reinforcement learning (IRL) method: Max Entropy Inverse Soft Constraint IRL (MESC-IRL), for learning implicit hard and soft constraints over states, actions, and state features from demonstrations in deterministic and non-deterministic environments modeled as Markov Decision Processes (MDPs). Our method enables agents implicitly learn human constraints and desires without the need for explicit modeling by the agent designer and to transfer these constraints between environments. Our novel method generalizes prior work which only considered deterministic hard constraints and achieves state of the art performance.

Combining Fast and Slow Thinking for Human-like and Efficient Navigation in Constrained Environments

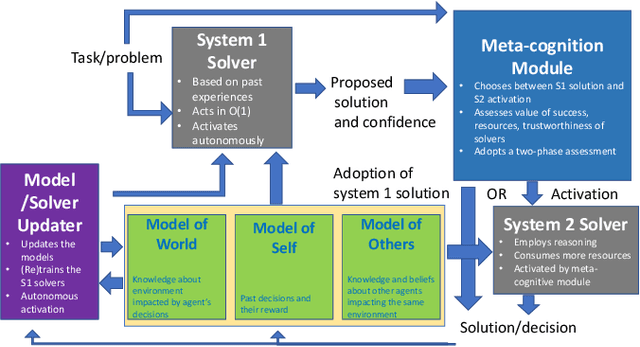
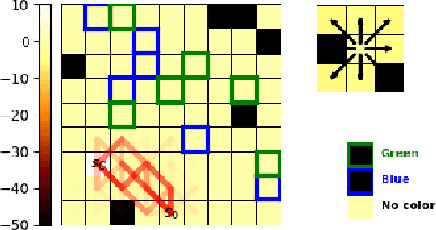
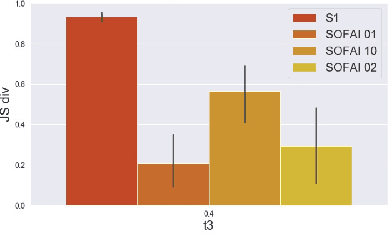
Current AI systems lack several important human capabilities, such as adaptability, generalizability, self-control, consistency, common sense, and causal reasoning. We believe that existing cognitive theories of human decision making, such as the thinking fast and slow theory, can provide insights on how to advance AI systems towards some of these capabilities. In this paper, we propose a general architecture that is based on fast/slow solvers and a metacognitive component. We then present experimental results on the behavior of an instance of this architecture, for AI systems that make decisions about navigating in a constrained environment. We show how combining the fast and slow decision modalities allows the system to evolve over time and gradually pass from slow to fast thinking with enough experience, and that this greatly helps in decision quality, resource consumption, and efficiency.

Stable marriage problems with quantitative preferences

The stable marriage problem is a well-known problem of matching men to women so that no man and woman, who are not married to each other, both prefer each other. Such a problem has a wide variety of practical applications, ranging from matching resident doctors to hospitals, to matching students to schools or more generally to any two-sided market. In the classical stable marriage problem, both men and women express a strict preference order over the members of the other sex, in a qualitative way. Here we consider stable marriage problems with quantitative preferences: each man (resp., woman) provides a score for each woman (resp., man). Such problems are more expressive than the classical stable marriage problems. Moreover, in some real-life situations it is more natural to express scores (to model, for example, profits or costs) rather than a qualitative preference ordering. In this context, we define new notions of stability and optimality, and we provide algorithms to find marriages which are stable and/or optimal according to these notions. While expressivity greatly increases by adopting quantitative preferences, we show that in most cases the desired solutions can be found by adapting existing algorithms for the classical stable marriage problem.

Elicitation strategies for fuzzy constraint problems with missing preferences: algorithms and experimental studies

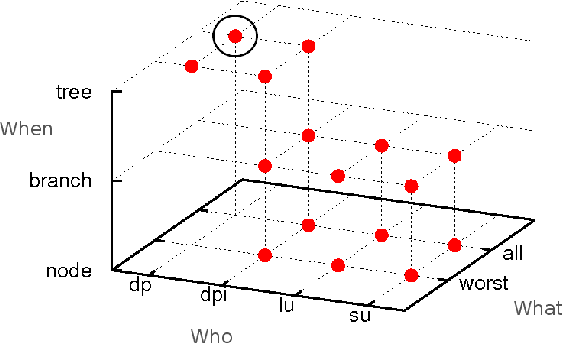
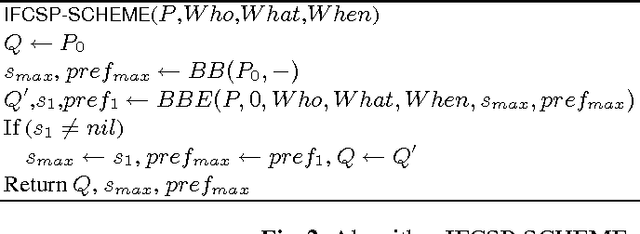
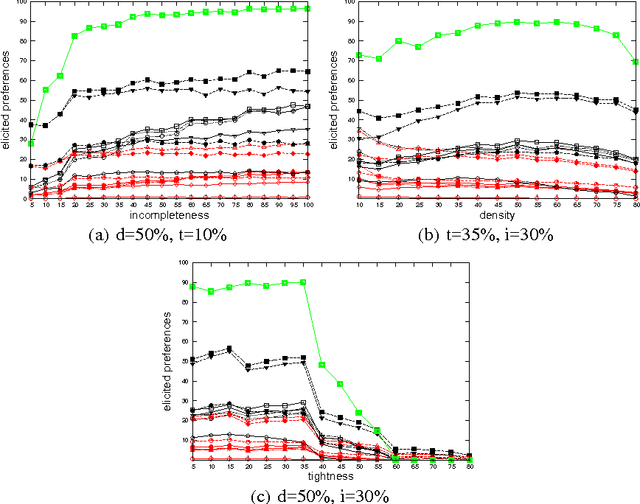
Fuzzy constraints are a popular approach to handle preferences and over-constrained problems in scenarios where one needs to be cautious, such as in medical or space applications. We consider here fuzzy constraint problems where some of the preferences may be missing. This models, for example, settings where agents are distributed and have privacy issues, or where there is an ongoing preference elicitation process. In this setting, we study how to find a solution which is optimal irrespective of the missing preferences. In the process of finding such a solution, we may elicit preferences from the user if necessary. However, our goal is to ask the user as little as possible. We define a combined solving and preference elicitation scheme with a large number of different instantiations, each corresponding to a concrete algorithm which we compare experimentally. We compute both the number of elicited preferences and the "user effort", which may be larger, as it contains all the preference values the user has to compute to be able to respond to the elicitation requests. While the number of elicited preferences is important when the concern is to communicate as little information as possible, the user effort measures also the hidden work the user has to do to be able to communicate the elicited preferences. Our experimental results show that some of our algorithms are very good at finding a necessarily optimal solution while asking the user for only a very small fraction of the missing preferences. The user effort is also very small for the best algorithms. Finally, we test these algorithms on hard constraint problems with possibly missing constraints, where the aim is to find feasible solutions irrespective of the missing constraints.

Dealing with incomplete agents' preferences and an uncertain agenda in group decision making via sequential majority voting

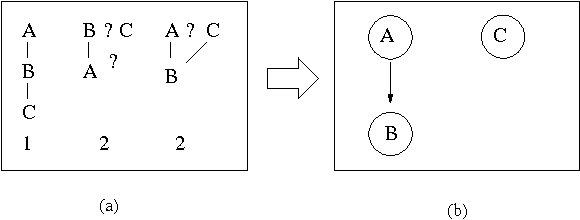
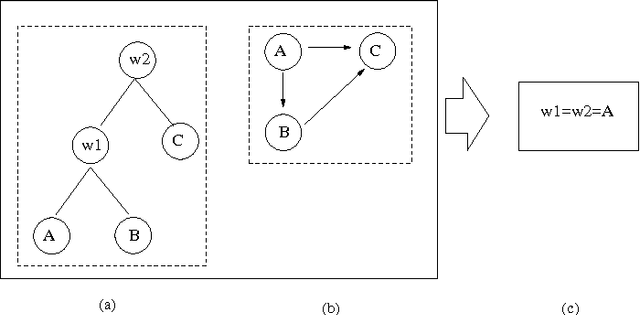
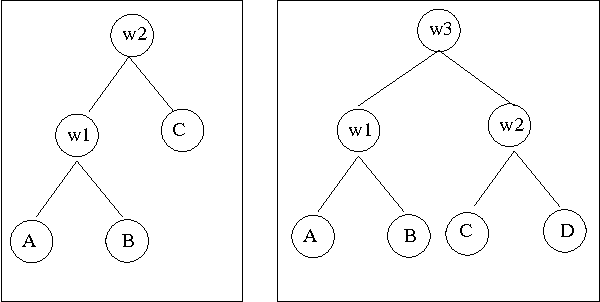
We consider multi-agent systems where agents' preferences are aggregated via sequential majority voting: each decision is taken by performing a sequence of pairwise comparisons where each comparison is a weighted majority vote among the agents. Incompleteness in the agents' preferences is common in many real-life settings due to privacy issues or an ongoing elicitation process. In addition, there may be uncertainty about how the preferences are aggregated. For example, the agenda (a tree whose leaves are labelled with the decisions being compared) may not yet be known or fixed. We therefore study how to determine collectively optimal decisions (also called winners) when preferences may be incomplete, and when the agenda may be uncertain. We show that it is computationally easy to determine if a candidate decision always wins, or may win, whatever the agenda. On the other hand, it is computationally hard to know wheth er a candidate decision wins in at least one agenda for at least one completion of the agents' preferences. These results hold even if the agenda must be balanced so that each candidate decision faces the same number of majority votes. Such results are useful for reasoning about preference elicitation. They help understand the complexity of tasks such as determining if a decision can be taken collectively, as well as knowing if the winner can be manipulated by appropriately ordering the agenda.

Manipulation and gender neutrality in stable marriage procedures

The stable marriage problem is a well-known problem of matching men to women so that no man and woman who are not married to each other both prefer each other. Such a problem has a wide variety of practical applications ranging from matching resident doctors to hospitals to matching students to schools. A well-known algorithm to solve this problem is the Gale-Shapley algorithm, which runs in polynomial time. It has been proven that stable marriage procedures can always be manipulated. Whilst the Gale-Shapley algorithm is computationally easy to manipulate, we prove that there exist stable marriage procedures which are NP-hard to manipulate. We also consider the relationship between voting theory and stable marriage procedures, showing that voting rules which are NP-hard to manipulate can be used to define stable marriage procedures which are themselves NP-hard to manipulate. Finally, we consider the issue that stable marriage procedures like Gale-Shapley favour one gender over the other, and we show how to use voting rules to make any stable marriage procedure gender neutral.