Elicitation strategies for fuzzy constraint problems with missing preferences: algorithms and experimental studies

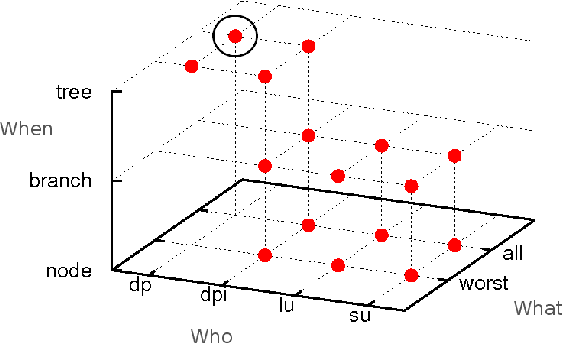
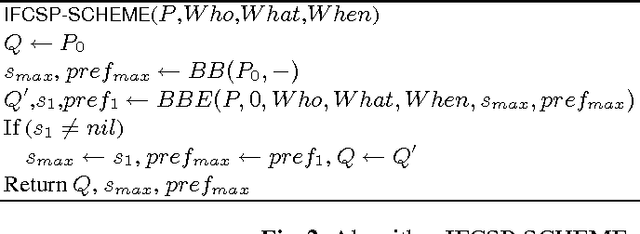
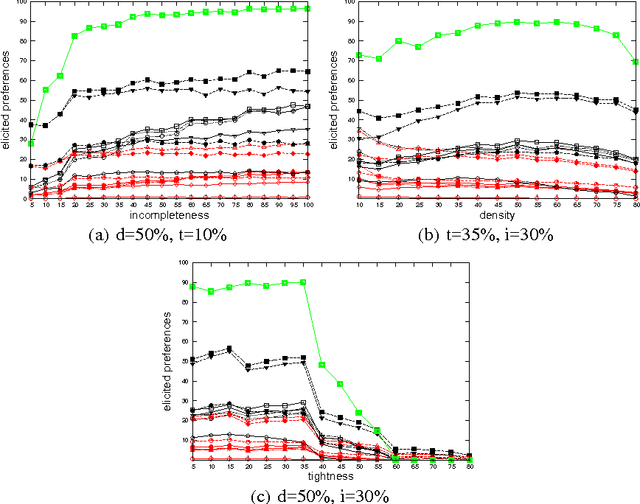
Fuzzy constraints are a popular approach to handle preferences and over-constrained problems in scenarios where one needs to be cautious, such as in medical or space applications. We consider here fuzzy constraint problems where some of the preferences may be missing. This models, for example, settings where agents are distributed and have privacy issues, or where there is an ongoing preference elicitation process. In this setting, we study how to find a solution which is optimal irrespective of the missing preferences. In the process of finding such a solution, we may elicit preferences from the user if necessary. However, our goal is to ask the user as little as possible. We define a combined solving and preference elicitation scheme with a large number of different instantiations, each corresponding to a concrete algorithm which we compare experimentally. We compute both the number of elicited preferences and the "user effort", which may be larger, as it contains all the preference values the user has to compute to be able to respond to the elicitation requests. While the number of elicited preferences is important when the concern is to communicate as little information as possible, the user effort measures also the hidden work the user has to do to be able to communicate the elicited preferences. Our experimental results show that some of our algorithms are very good at finding a necessarily optimal solution while asking the user for only a very small fraction of the missing preferences. The user effort is also very small for the best algorithms. Finally, we test these algorithms on hard constraint problems with possibly missing constraints, where the aim is to find feasible solutions irrespective of the missing constraints.

Dealing with incomplete agents' preferences and an uncertain agenda in group decision making via sequential majority voting

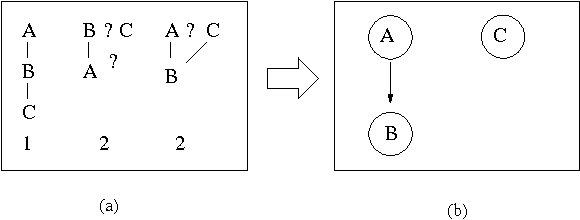
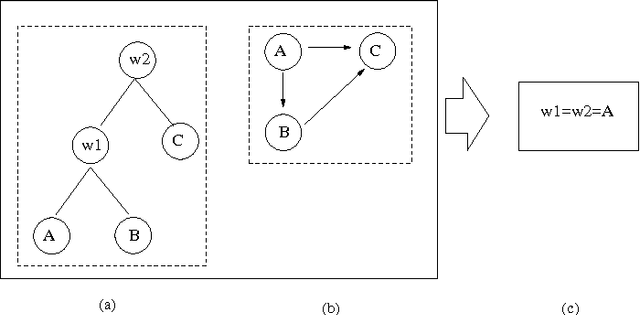
We consider multi-agent systems where agents' preferences are aggregated via sequential majority voting: each decision is taken by performing a sequence of pairwise comparisons where each comparison is a weighted majority vote among the agents. Incompleteness in the agents' preferences is common in many real-life settings due to privacy issues or an ongoing elicitation process. In addition, there may be uncertainty about how the preferences are aggregated. For example, the agenda (a tree whose leaves are labelled with the decisions being compared) may not yet be known or fixed. We therefore study how to determine collectively optimal decisions (also called winners) when preferences may be incomplete, and when the agenda may be uncertain. We show that it is computationally easy to determine if a candidate decision always wins, or may win, whatever the agenda. On the other hand, it is computationally hard to know wheth er a candidate decision wins in at least one agenda for at least one completion of the agents' preferences. These results hold even if the agenda must be balanced so that each candidate decision faces the same number of majority votes. Such results are useful for reasoning about preference elicitation. They help understand the complexity of tasks such as determining if a decision can be taken collectively, as well as knowing if the winner can be manipulated by appropriately ordering the agenda.

Manipulation and gender neutrality in stable marriage procedures

The stable marriage problem is a well-known problem of matching men to women so that no man and woman who are not married to each other both prefer each other. Such a problem has a wide variety of practical applications ranging from matching resident doctors to hospitals to matching students to schools. A well-known algorithm to solve this problem is the Gale-Shapley algorithm, which runs in polynomial time. It has been proven that stable marriage procedures can always be manipulated. Whilst the Gale-Shapley algorithm is computationally easy to manipulate, we prove that there exist stable marriage procedures which are NP-hard to manipulate. We also consider the relationship between voting theory and stable marriage procedures, showing that voting rules which are NP-hard to manipulate can be used to define stable marriage procedures which are themselves NP-hard to manipulate. Finally, we consider the issue that stable marriage procedures like Gale-Shapley favour one gender over the other, and we show how to use voting rules to make any stable marriage procedure gender neutral.