Mirco Gelain
Local search for stable marriage problems with ties and incomplete lists
Jul 05, 2010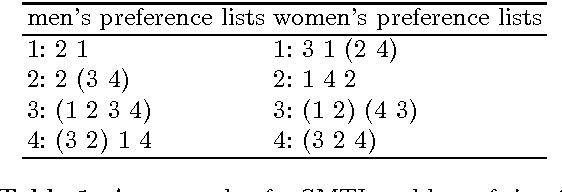
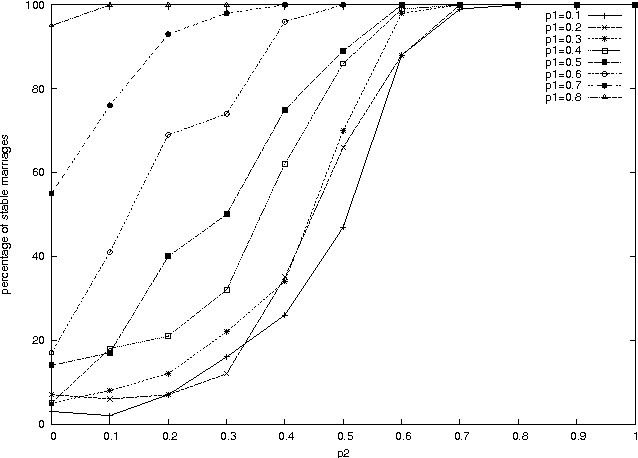
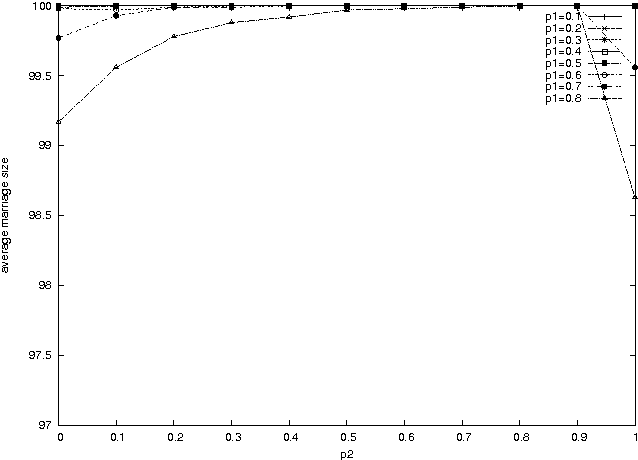
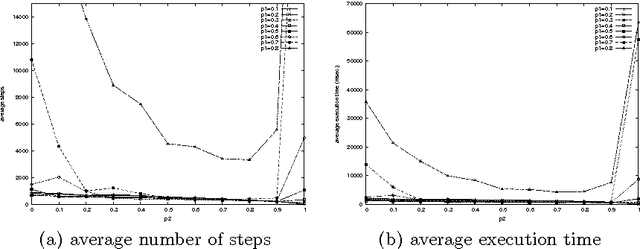
Abstract:The stable marriage problem has a wide variety of practical applications, ranging from matching resident doctors to hospitals, to matching students to schools, or more generally to any two-sided market. We consider a useful variation of the stable marriage problem, where the men and women express their preferences using a preference list with ties over a subset of the members of the other sex. Matchings are permitted only with people who appear in these preference lists. In this setting, we study the problem of finding a stable matching that marries as many people as possible. Stability is an envy-free notion: no man and woman who are not married to each other would both prefer each other to their partners or to being single. This problem is NP-hard. We tackle this problem using local search, exploiting properties of the problem to reduce the size of the neighborhood and to make local moves efficiently. Experimental results show that this approach is able to solve large problems, quickly returning stable matchings of large and often optimal size.
Elicitation strategies for fuzzy constraint problems with missing preferences: algorithms and experimental studies
Sep 24, 2009
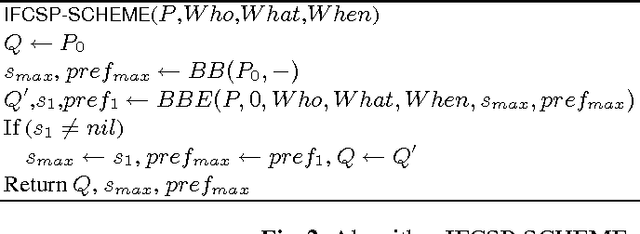

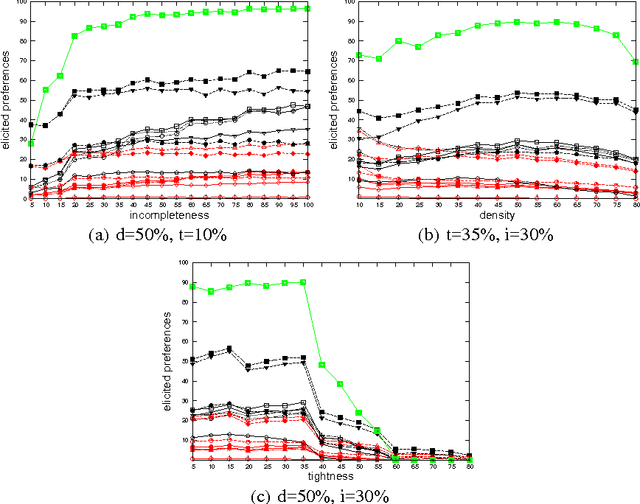
Abstract:Fuzzy constraints are a popular approach to handle preferences and over-constrained problems in scenarios where one needs to be cautious, such as in medical or space applications. We consider here fuzzy constraint problems where some of the preferences may be missing. This models, for example, settings where agents are distributed and have privacy issues, or where there is an ongoing preference elicitation process. In this setting, we study how to find a solution which is optimal irrespective of the missing preferences. In the process of finding such a solution, we may elicit preferences from the user if necessary. However, our goal is to ask the user as little as possible. We define a combined solving and preference elicitation scheme with a large number of different instantiations, each corresponding to a concrete algorithm which we compare experimentally. We compute both the number of elicited preferences and the "user effort", which may be larger, as it contains all the preference values the user has to compute to be able to respond to the elicitation requests. While the number of elicited preferences is important when the concern is to communicate as little information as possible, the user effort measures also the hidden work the user has to do to be able to communicate the elicited preferences. Our experimental results show that some of our algorithms are very good at finding a necessarily optimal solution while asking the user for only a very small fraction of the missing preferences. The user effort is also very small for the best algorithms. Finally, we test these algorithms on hard constraint problems with possibly missing constraints, where the aim is to find feasible solutions irrespective of the missing constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge