Voting with Random Classifiers (VORACE)

In many machine learning scenarios, looking for the best classifier that fits a particular dataset can be very costly in terms of time and resources. Moreover, it can require deep knowledge of the specific domain. We propose a new technique which does not require profound expertise in the domain and avoids the commonly used strategy of hyper-parameter tuning and model selection. Our method is an innovative ensemble technique that uses voting rules over a set of randomly-generated classifiers. Given a new input sample, we interpret the output of each classifier as a ranking over the set of possible classes. We then aggregate these output rankings using a voting rule, which treats them as preferences over the classes. We show that our approach obtains good results compared to the state-of-the-art, both providing a theoretical analysis and an empirical evaluation of the approach on several datasets.

Stable marriage problems with quantitative preferences

The stable marriage problem is a well-known problem of matching men to women so that no man and woman, who are not married to each other, both prefer each other. Such a problem has a wide variety of practical applications, ranging from matching resident doctors to hospitals, to matching students to schools or more generally to any two-sided market. In the classical stable marriage problem, both men and women express a strict preference order over the members of the other sex, in a qualitative way. Here we consider stable marriage problems with quantitative preferences: each man (resp., woman) provides a score for each woman (resp., man). Such problems are more expressive than the classical stable marriage problems. Moreover, in some real-life situations it is more natural to express scores (to model, for example, profits or costs) rather than a qualitative preference ordering. In this context, we define new notions of stability and optimality, and we provide algorithms to find marriages which are stable and/or optimal according to these notions. While expressivity greatly increases by adopting quantitative preferences, we show that in most cases the desired solutions can be found by adapting existing algorithms for the classical stable marriage problem.

Local search for stable marriage problems with ties and incomplete lists

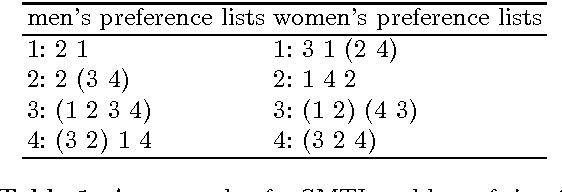
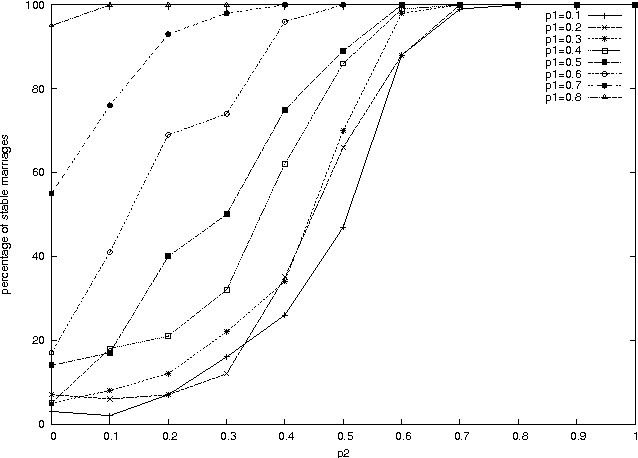
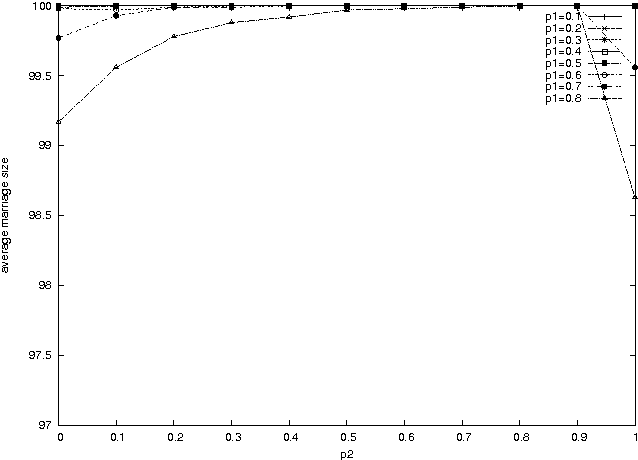
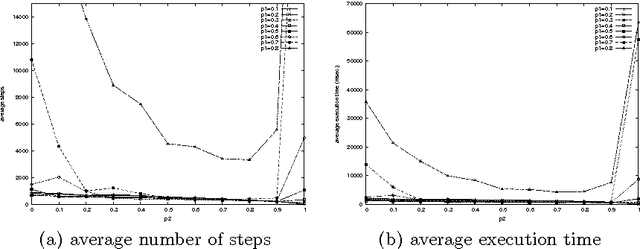
The stable marriage problem has a wide variety of practical applications, ranging from matching resident doctors to hospitals, to matching students to schools, or more generally to any two-sided market. We consider a useful variation of the stable marriage problem, where the men and women express their preferences using a preference list with ties over a subset of the members of the other sex. Matchings are permitted only with people who appear in these preference lists. In this setting, we study the problem of finding a stable matching that marries as many people as possible. Stability is an envy-free notion: no man and woman who are not married to each other would both prefer each other to their partners or to being single. This problem is NP-hard. We tackle this problem using local search, exploiting properties of the problem to reduce the size of the neighborhood and to make local moves efficiently. Experimental results show that this approach is able to solve large problems, quickly returning stable matchings of large and often optimal size.