Toward End-to-End Bearing Fault Diagnosis for Industrial Scenarios with Spiking Neural Networks

Spiking neural networks (SNNs) transmit information via low-power binary spikes and have received widespread attention in areas such as computer vision and reinforcement learning. However, there have been very few explorations of SNNs in more practical industrial scenarios. In this paper, we focus on the application of SNNs in bearing fault diagnosis to facilitate the integration of high-performance AI algorithms and real-world industries. In particular, we identify two key limitations of existing SNN fault diagnosis methods: inadequate encoding capacity that necessitates cumbersome data preprocessing, and non-spike-oriented architectures that constrain the performance of SNNs. To alleviate these problems, we propose a Multi-scale Residual Attention SNN (MRA-SNN) to simultaneously improve the efficiency, performance, and robustness of SNN methods. By incorporating a lightweight attention mechanism, we have designed a multi-scale attention encoding module to extract multiscale fault features from vibration signals and encode them as spatio-temporal spikes, eliminating the need for complicated preprocessing. Then, the spike residual attention block extracts high-dimensional fault features and enhances the expressiveness of sparse spikes with the attention mechanism for end-to-end diagnosis. In addition, the performance and robustness of MRA-SNN is further enhanced by introducing the lightweight attention mechanism within the spiking neurons to simulate the biological dendritic filtering effect. Extensive experiments on MFPT and JNU benchmark datasets demonstrate that MRA-SNN significantly outperforms existing methods in terms of accuracy, energy consumption and noise robustness, and is more feasible for deployment in real-world industrial scenarios.

Harvesting Ambient RF for Presence Detection Through Deep Learning

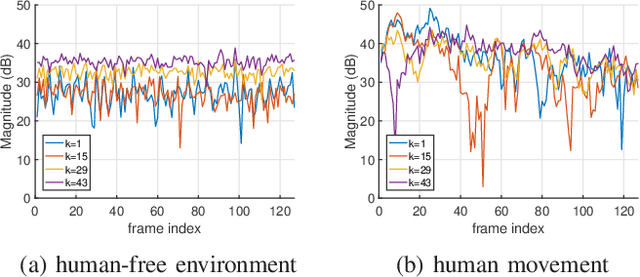
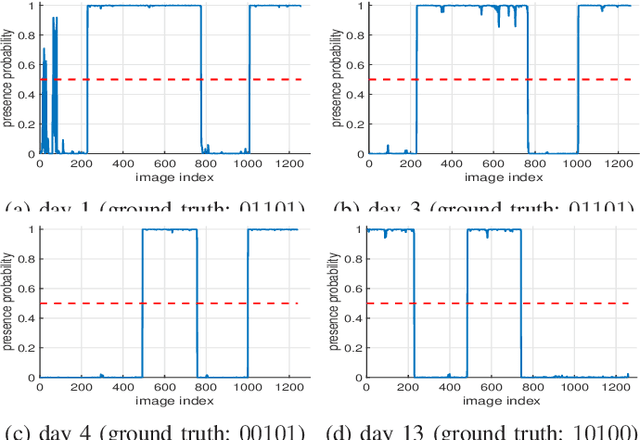
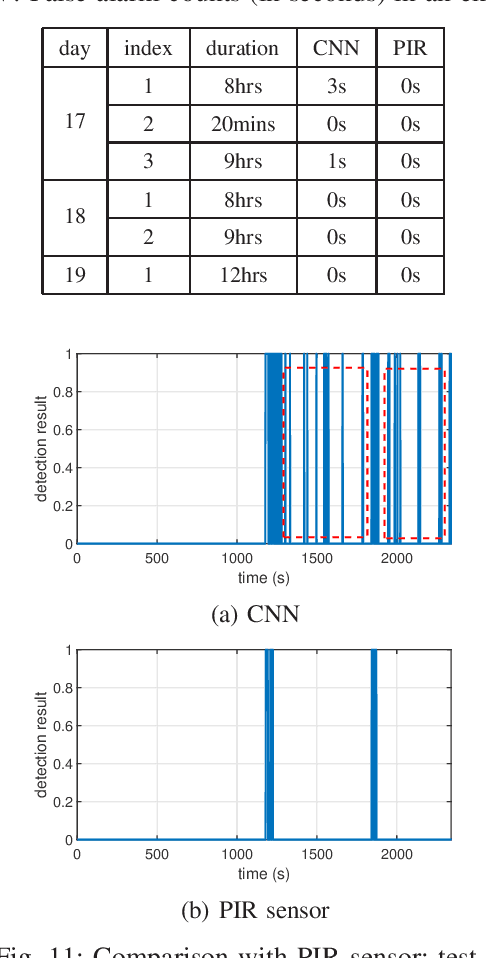
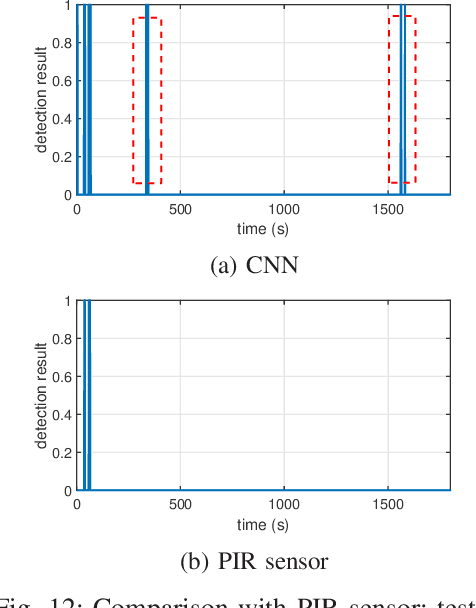
This paper explores the use of ambient radio frequency (RF) signals for human presence detection through deep learning. Using WiFi signal as an example, we demonstrate that the channel state information (CSI) obtained at the receiver contains rich information about the propagation environment. Through judicious pre-processing of the estimated CSI followed by deep learning, reliable presence detection can be achieved. Several challenges in passive RF sensing are addressed. With presence detection, how to collect training data with human presence can have a significant impact on the performance. This is in contrast to activity detection when a specific motion pattern is of interest. A second challenge is that RF signals are complex-valued. Handling complex-valued input in deep learning requires careful data representation and network architecture design. Finally, human presence affects CSI variation along multiple dimensions; such variation, however, is often masked by system impediments such as timing or frequency offset. Addressing these challenges, the proposed learning system uses pre-processing to preserve human motion induced channel variation while insulating against other impairments. A convolutional neural network (CNN) properly trained with both magnitude and phase information is then designed to achieve reliable presence detection. Extensive experiments are conducted. Using off-the-shelf WiFi devices, the proposed deep learning based RF sensing achieves near perfect presence detection during multiple extended periods of test and exhibits superior performance compared with leading edge passive infrared sensors. The learning based passive RF sensing thus provides a viable and promising alternative for presence or occupancy detection.

FOCUS: Dealing with Label Quality Disparity in Federated Learning

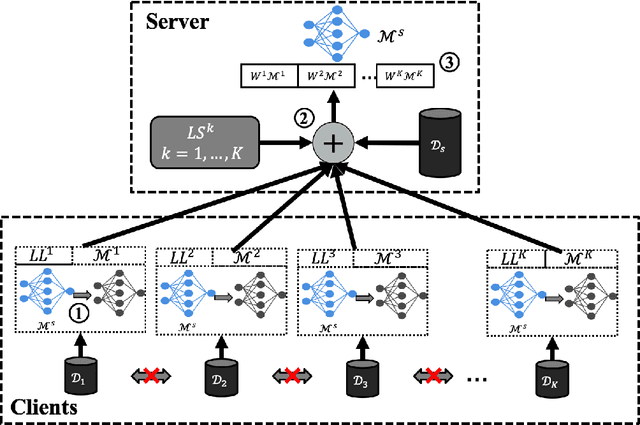
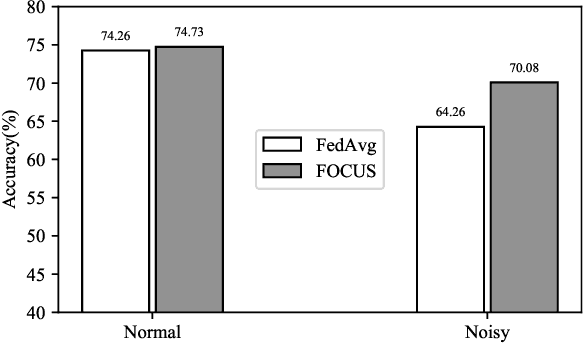
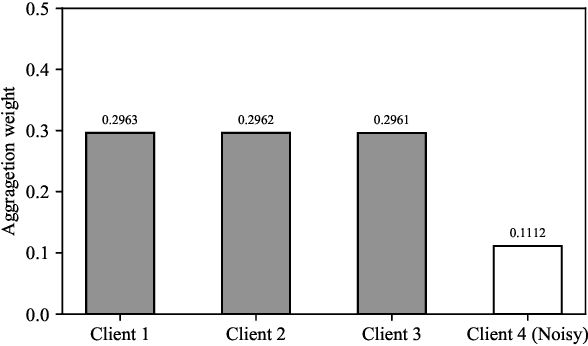
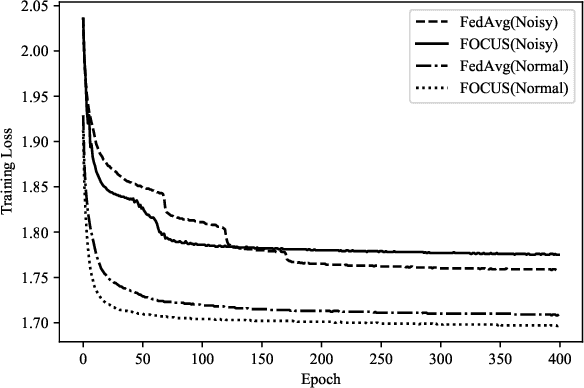
Ubiquitous systems with End-Edge-Cloud architecture are increasingly being used in healthcare applications. Federated Learning (FL) is highly useful for such applications, due to silo effect and privacy preserving. Existing FL approaches generally do not account for disparities in the quality of local data labels. However, the clients in ubiquitous systems tend to suffer from label noise due to varying skill-levels, biases or malicious tampering of the annotators. In this paper, we propose Federated Opportunistic Computing for Ubiquitous Systems (FOCUS) to address this challenge. It maintains a small set of benchmark samples on the FL server and quantifies the credibility of the client local data without directly observing them by computing the mutual cross-entropy between performance of the FL model on the local datasets and that of the client local FL model on the benchmark dataset. Then, a credit weighted orchestration is performed to adjust the weight assigned to clients in the FL model based on their credibility values. FOCUS has been experimentally evaluated on both synthetic data and real-world data. The results show that it effectively identifies clients with noisy labels and reduces their impact on the model performance, thereby significantly outperforming existing FL approaches.

Asymptotically Optimal One- and Two-Sample Testing with Kernels

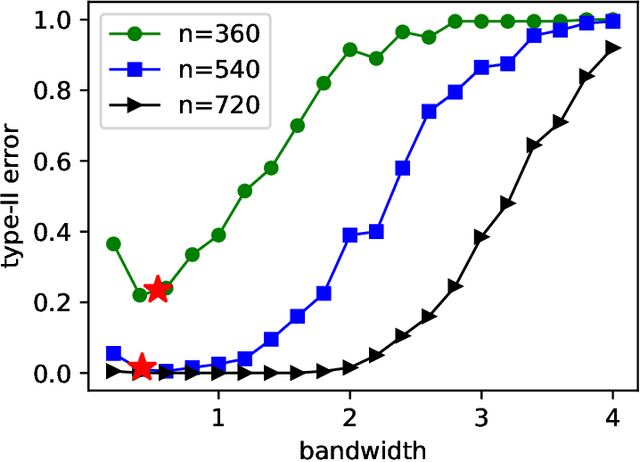
We characterize the asymptotic performance of nonparametric one- and two-sample testing. The exponential decay rate or error exponent of the type-II error probability is used as the asymptotic performance metric, and an optimal test achieves the maximum rate subject to a constant level constraint on the type-I error probability. With Sanov's theorem, we derive a sufficient condition for one-sample tests to achieve the optimal error exponent in the universal setting, i.e., for any distribution defining the alternative hypothesis. We then show that two classes of Maximum Mean Discrepancy (MMD) based tests attain the optimal type-II error exponent on $\mathbb R^d$, while the quadratic-time Kernel Stein Discrepancy (KSD) based tests achieve this optimality with an asymptotic level constraint. For general two-sample testing, however, Sanov's theorem is insufficient to obtain a similar sufficient condition. We proceed to establish an extended version of Sanov's theorem and derive an exact error exponent for the quadratic-time MMD based two-sample tests. The obtained error exponent is further shown to be optimal among all two-sample tests satisfying a given level constraint. Our results not only solve a long-standing open problem in information theory and statistics, but also provide an achievability result for optimal nonparametric one- and two-sample testing. Application to off-line change detection and related issues are also discussed.

K-medoids Clustering of Data Sequences with Composite Distributions

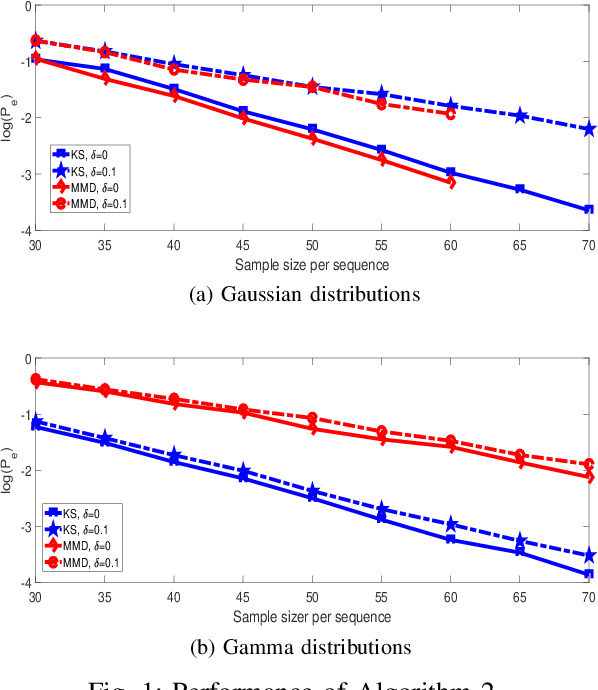
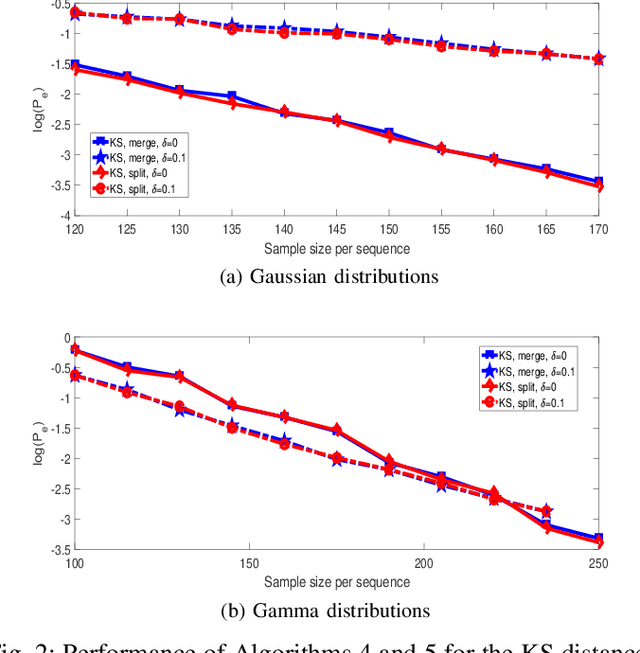
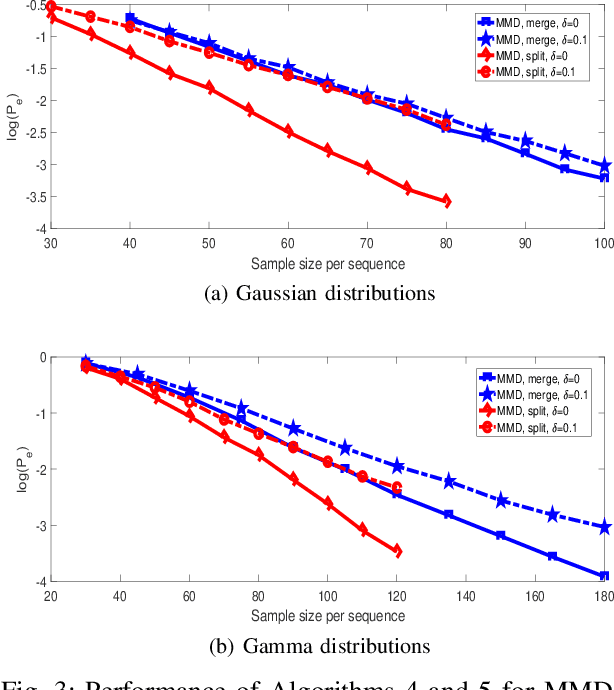
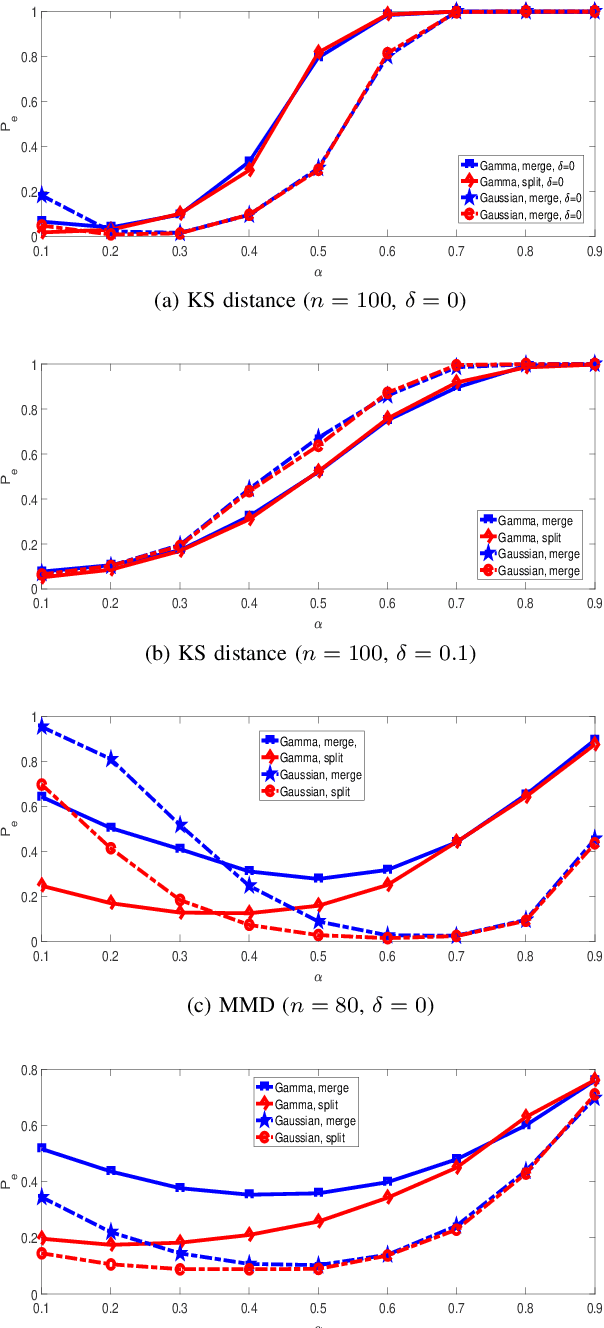
This paper studies clustering of data sequences using the k-medoids algorithm. All the data sequences are assumed to be generated from \emph{unknown} continuous distributions, which form clusters with each cluster containing a composite set of closely located distributions (based on a certain distance metric between distributions). The maximum intra-cluster distance is assumed to be smaller than the minimum inter-cluster distance, and both values are assumed to be known. The goal is to group the data sequences together if their underlying generative distributions (which are unknown) belong to one cluster. Distribution distance metrics based k-medoids algorithms are proposed for known and unknown number of distribution clusters. Upper bounds on the error probability and convergence results in the large sample regime are also provided. It is shown that the error probability decays exponentially fast as the number of samples in each data sequence goes to infinity. The error exponent has a simple form regardless of the distance metric applied when certain conditions are satisfied. In particular, the error exponent is characterized when either the Kolmogrov-Smirnov distance or the maximum mean discrepancy are used as the distance metric. Simulation results are provided to validate the analysis.

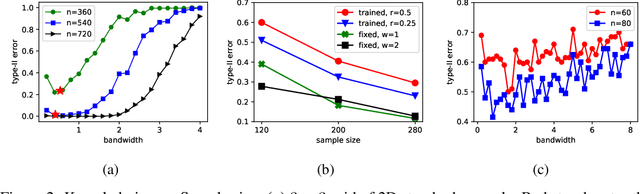
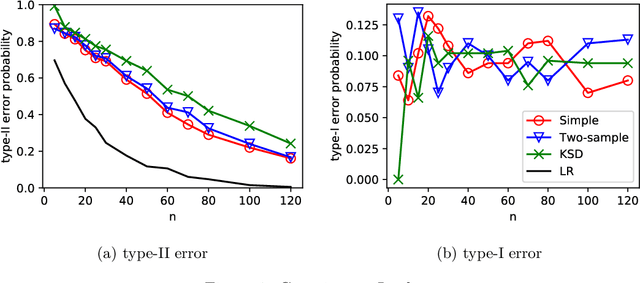
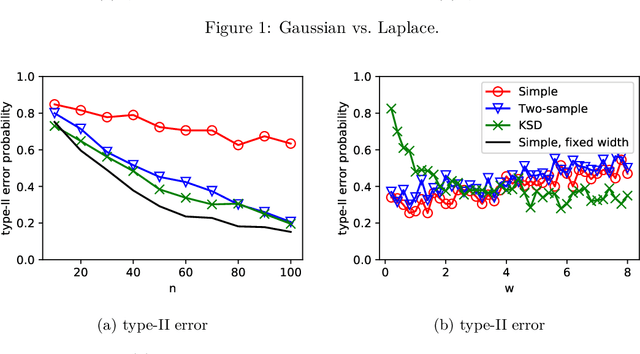
Universal Hypothesis Testing with Kernels: Asymptotically Optimal Tests for Goodness of Fit

We characterize the asymptotic performance of nonparametric goodness of fit testing, otherwise known as universal hypothesis testing in information theory and statistics. The exponential decay rate of the type-II error probability is used as the asymptotic performance metric, and an optimal test achieves the maximum rate subject to a constant level constraint on the type-I error probability. We show that two classes of Maximum Mean Discrepancy (MMD) based tests attain this optimality on $\mathbb R^d$, while the quadratic-time Kernel Stein Discrepancy (KSD) based tests achieve the same exponential decay rate under an asymptotic level constraint. With bootstrap thresholds, these kernel based tests have similar statistical performance in our experiments of finite samples. Key to our approach are Sanov's theorem~in large deviation theory and the weak convergence properties of the MMD and KSD.

Exponentially Consistent Kernel Two-Sample Tests

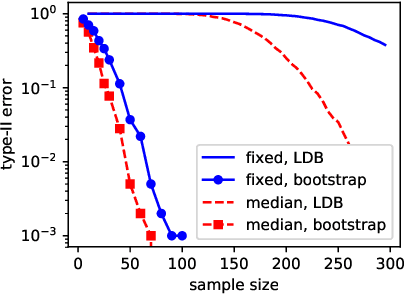
Given two sets of independent samples from unknown distributions $P$ and $Q$, a two-sample test decides whether to reject the null hypothesis that $P=Q$. Recent attention has focused on kernel two-sample tests as the test statistics are easy to compute, converge fast, and have low bias with their finite sample estimates. However, there still lacks an exact characterization on the asymptotic performance of such tests, and in particular, the rate at which the type-II error probability decays to zero in the large sample limit. In this work, we establish that a class of kernel two-sample tests are exponentially consistent with Polish, locally compact Hausdorff sample space, e.g., $\mathbb R^d$. The obtained exponential decay rate is further shown to be optimal among all two-sample tests satisfying the level constraint, and is independent of particular kernels provided that they are bounded continuous and characteristic. Our results gain new insights into related issues such as fair alternative for testing and kernel selection strategy. Finally, as an application, we show that a kernel based test achieves the optimal detection for off-line change detection in the nonparametric setting.

Autonomous Localization and Mapping Using a Single Mobile Device

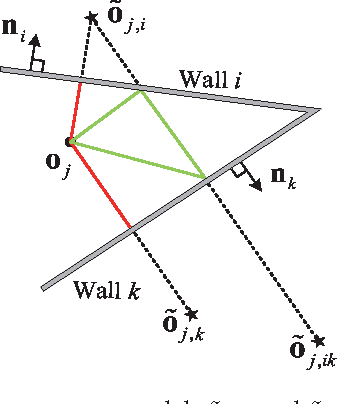
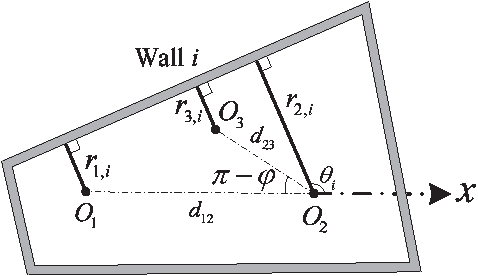
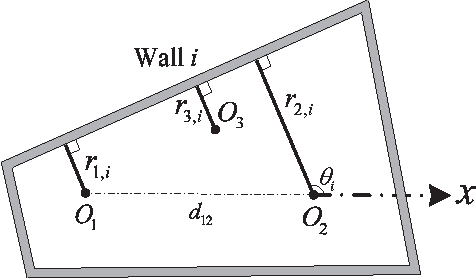
This paper considers the problem of simultaneous 2-D room shape reconstruction and self-localization without the requirement of any pre-established infrastructure. A mobile device equipped with co-located microphone and loudspeaker as well as internal motion sensors is used to emit acoustic pulses and collect echoes reflected by the walls. Using only first order echoes, room shape recovery and self-localization is feasible when auxiliary information is obtained using motion sensors. In particular, it is established that using echoes collected at three measurement locations and the two distances between consecutive measurement points, unique localization and mapping can be achieved provided that the three measurement points are not collinear. Practical algorithms for room shape reconstruction and self-localization in the presence of noise and higher order echoes are proposed along with experimental results to demonstrate the effectiveness of the proposed approach.