Exponentially Consistent Kernel Two-Sample Tests
Paper and Code
May 21, 2018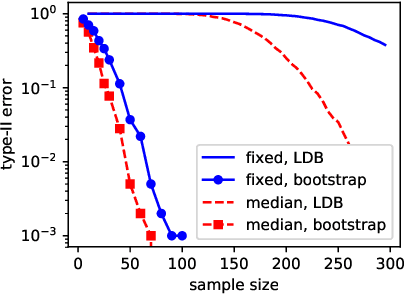
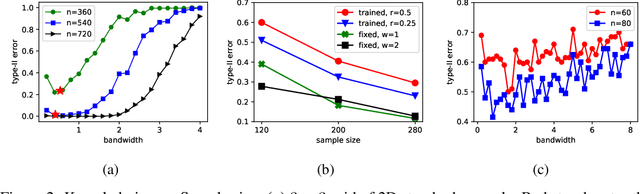
Given two sets of independent samples from unknown distributions $P$ and $Q$, a two-sample test decides whether to reject the null hypothesis that $P=Q$. Recent attention has focused on kernel two-sample tests as the test statistics are easy to compute, converge fast, and have low bias with their finite sample estimates. However, there still lacks an exact characterization on the asymptotic performance of such tests, and in particular, the rate at which the type-II error probability decays to zero in the large sample limit. In this work, we establish that a class of kernel two-sample tests are exponentially consistent with Polish, locally compact Hausdorff sample space, e.g., $\mathbb R^d$. The obtained exponential decay rate is further shown to be optimal among all two-sample tests satisfying the level constraint, and is independent of particular kernels provided that they are bounded continuous and characteristic. Our results gain new insights into related issues such as fair alternative for testing and kernel selection strategy. Finally, as an application, we show that a kernel based test achieves the optimal detection for off-line change detection in the nonparametric setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge