Universal Hypothesis Testing with Kernels: Asymptotically Optimal Tests for Goodness of Fit

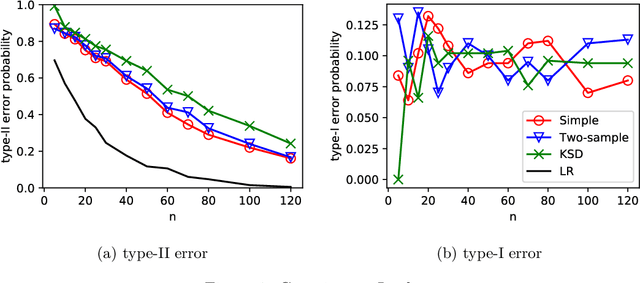
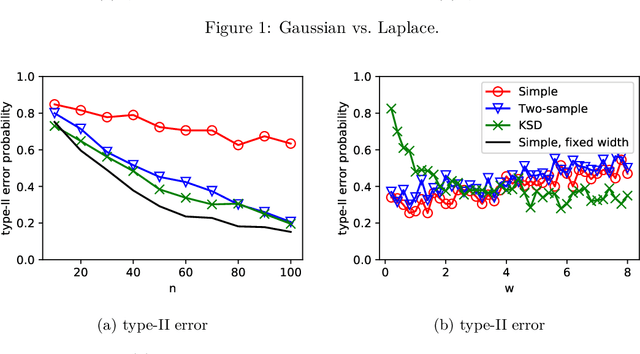
We characterize the asymptotic performance of nonparametric goodness of fit testing, otherwise known as universal hypothesis testing in information theory and statistics. The exponential decay rate of the type-II error probability is used as the asymptotic performance metric, and an optimal test achieves the maximum rate subject to a constant level constraint on the type-I error probability. We show that two classes of Maximum Mean Discrepancy (MMD) based tests attain this optimality on $\mathbb R^d$, while the quadratic-time Kernel Stein Discrepancy (KSD) based tests achieve the same exponential decay rate under an asymptotic level constraint. With bootstrap thresholds, these kernel based tests have similar statistical performance in our experiments of finite samples. Key to our approach are Sanov's theorem~in large deviation theory and the weak convergence properties of the MMD and KSD.