Understanding the performance gap between online and offline alignment algorithms

Reinforcement learning from human feedback (RLHF) is the canonical framework for large language model alignment. However, rising popularity in offline alignment algorithms challenge the need for on-policy sampling in RLHF. Within the context of reward over-optimization, we start with an opening set of experiments that demonstrate the clear advantage of online methods over offline methods. This prompts us to investigate the causes to the performance discrepancy through a series of carefully designed experimental ablations. We show empirically that hypotheses such as offline data coverage and data quality by itself cannot convincingly explain the performance difference. We also find that while offline algorithms train policy to become good at pairwise classification, it is worse at generations; in the meantime the policies trained by online algorithms are good at generations while worse at pairwise classification. This hints at a unique interplay between discriminative and generative capabilities, which is greatly impacted by the sampling process. Lastly, we observe that the performance discrepancy persists for both contrastive and non-contrastive loss functions, and appears not to be addressed by simply scaling up policy networks. Taken together, our study sheds light on the pivotal role of on-policy sampling in AI alignment, and hints at certain fundamental challenges of offline alignment algorithms.

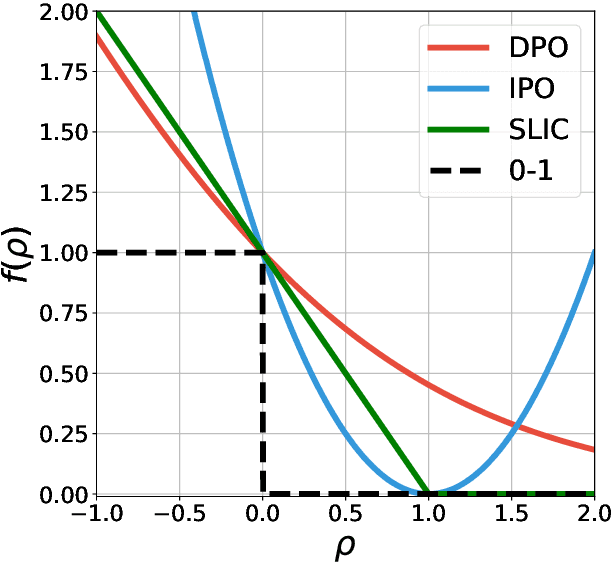
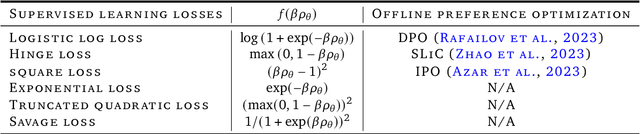
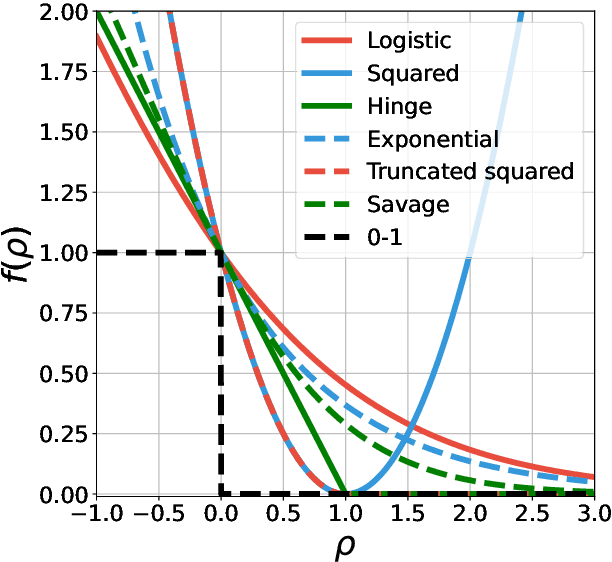
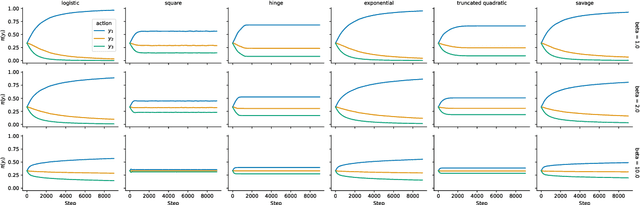
Generalized Preference Optimization: A Unified Approach to Offline Alignment

Offline preference optimization allows fine-tuning large models directly from offline data, and has proved effective in recent alignment practices. We propose generalized preference optimization (GPO), a family of offline losses parameterized by a general class of convex functions. GPO enables a unified view over preference optimization, encompassing existing algorithms such as DPO, IPO and SLiC as special cases, while naturally introducing new variants. The GPO framework also sheds light on how offline algorithms enforce regularization, through the design of the convex function that defines the loss. Our analysis and experiments reveal the connections and subtle differences between the offline regularization and the KL divergence regularization intended by the canonical RLHF formulation. In all, our results present new algorithmic toolkits and empirical insights to alignment practitioners.

Off-policy Distributional Q($λ$): Distributional RL without Importance Sampling

We introduce off-policy distributional Q($\lambda$), a new addition to the family of off-policy distributional evaluation algorithms. Off-policy distributional Q($\lambda$) does not apply importance sampling for off-policy learning, which introduces intriguing interactions with signed measures. Such unique properties distributional Q($\lambda$) from other existing alternatives such as distributional Retrace. We characterize the algorithmic properties of distributional Q($\lambda$) and validate theoretical insights with tabular experiments. We show how distributional Q($\lambda$)-C51, a combination of Q($\lambda$) with the C51 agent, exhibits promising results on deep RL benchmarks.

DoMo-AC: Doubly Multi-step Off-policy Actor-Critic Algorithm

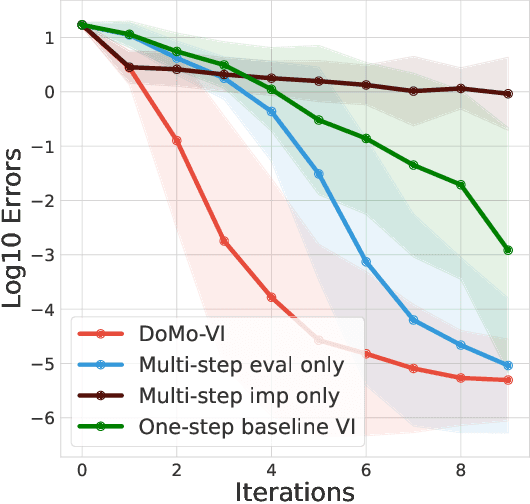
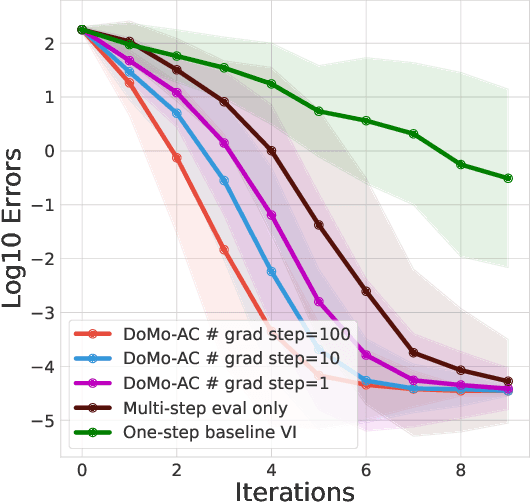
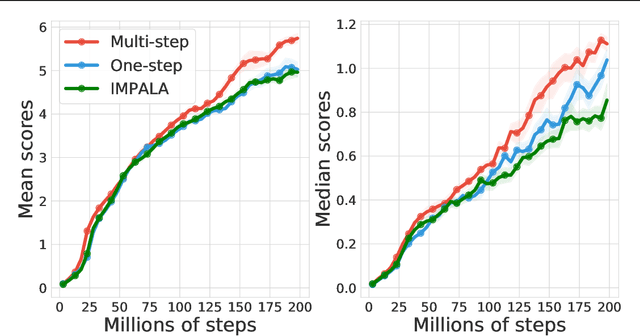
Multi-step learning applies lookahead over multiple time steps and has proved valuable in policy evaluation settings. However, in the optimal control case, the impact of multi-step learning has been relatively limited despite a number of prior efforts. Fundamentally, this might be because multi-step policy improvements require operations that cannot be approximated by stochastic samples, hence hindering the widespread adoption of such methods in practice. To address such limitations, we introduce doubly multi-step off-policy VI (DoMo-VI), a novel oracle algorithm that combines multi-step policy improvements and policy evaluations. DoMo-VI enjoys guaranteed convergence speed-up to the optimal policy and is applicable in general off-policy learning settings. We then propose doubly multi-step off-policy actor-critic (DoMo-AC), a practical instantiation of the DoMo-VI algorithm. DoMo-AC introduces a bias-variance trade-off that ensures improved policy gradient estimates. When combined with the IMPALA architecture, DoMo-AC has showed improvements over the baseline algorithm on Atari-57 game benchmarks.

Understanding Self-Predictive Learning for Reinforcement Learning

We study the learning dynamics of self-predictive learning for reinforcement learning, a family of algorithms that learn representations by minimizing the prediction error of their own future latent representations. Despite its recent empirical success, such algorithms have an apparent defect: trivial representations (such as constants) minimize the prediction error, yet it is obviously undesirable to converge to such solutions. Our central insight is that careful designs of the optimization dynamics are critical to learning meaningful representations. We identify that a faster paced optimization of the predictor and semi-gradient updates on the representation, are crucial to preventing the representation collapse. Then in an idealized setup, we show self-predictive learning dynamics carries out spectral decomposition on the state transition matrix, effectively capturing information of the transition dynamics. Building on the theoretical insights, we propose bidirectional self-predictive learning, a novel self-predictive algorithm that learns two representations simultaneously. We examine the robustness of our theoretical insights with a number of small-scale experiments and showcase the promise of the novel representation learning algorithm with large-scale experiments.

The Nature of Temporal Difference Errors in Multi-step Distributional Reinforcement Learning

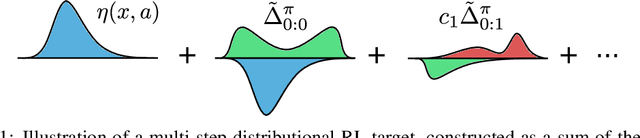
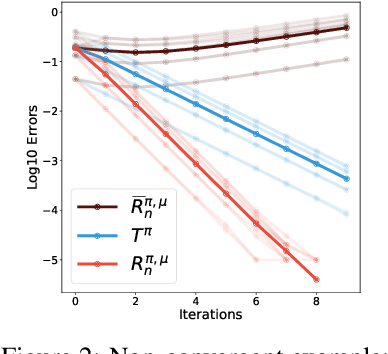
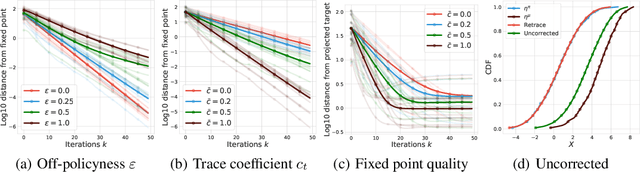
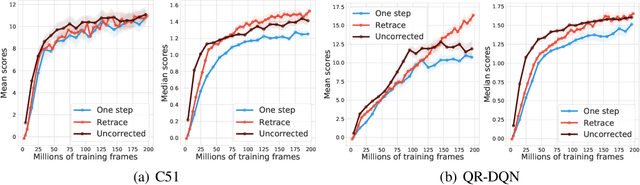
We study the multi-step off-policy learning approach to distributional RL. Despite the apparent similarity between value-based RL and distributional RL, our study reveals intriguing and fundamental differences between the two cases in the multi-step setting. We identify a novel notion of path-dependent distributional TD error, which is indispensable for principled multi-step distributional RL. The distinction from the value-based case bears important implications on concepts such as backward-view algorithms. Our work provides the first theoretical guarantees on multi-step off-policy distributional RL algorithms, including results that apply to the small number of existing approaches to multi-step distributional RL. In addition, we derive a novel algorithm, Quantile Regression-Retrace, which leads to a deep RL agent QR-DQN-Retrace that shows empirical improvements over QR-DQN on the Atari-57 benchmark. Collectively, we shed light on how unique challenges in multi-step distributional RL can be addressed both in theory and practice.

Multiclass Classification Calibration Functions

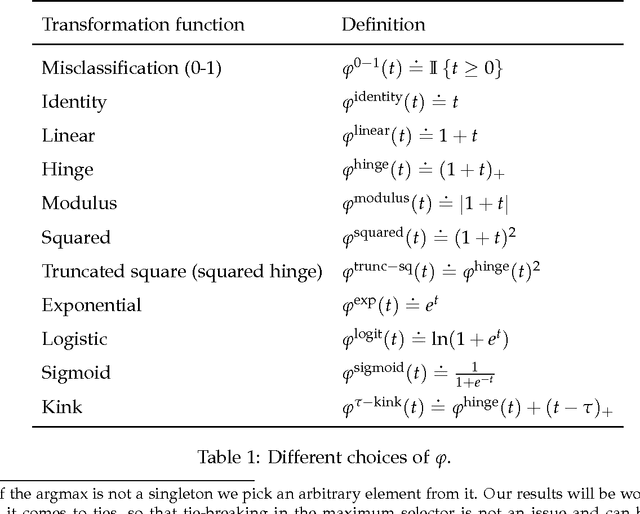
In this paper we refine the process of computing calibration functions for a number of multiclass classification surrogate losses. Calibration functions are a powerful tool for easily converting bounds for the surrogate risk (which can be computed through well-known methods) into bounds for the true risk, the probability of making a mistake. They are particularly suitable in non-parametric settings, where the approximation error can be controlled, and provide tighter bounds than the common technique of upper-bounding the 0-1 loss by the surrogate loss. The abstract nature of the more sophisticated existing calibration function results requires calibration functions to be explicitly derived on a case-by-case basis, requiring repeated efforts whenever bounds for a new surrogate loss are required. We devise a streamlined analysis that simplifies the process of deriving calibration functions for a large number of surrogate losses that have been proposed in the literature. The effort of deriving calibration functions is then surmised in verifying, for a chosen surrogate loss, a small number of conditions that we introduce. As case studies, we recover existing calibration functions for the well-known loss of Lee et al. (2004), and also provide novel calibration functions for well-known losses, including the one-versus-all loss and the logistic regression loss, plus a number of other losses that have been shown to be classification-calibrated in the past, but for which no calibration function had been derived.

Policy Error Bounds for Model-Based Reinforcement Learning with Factored Linear Models

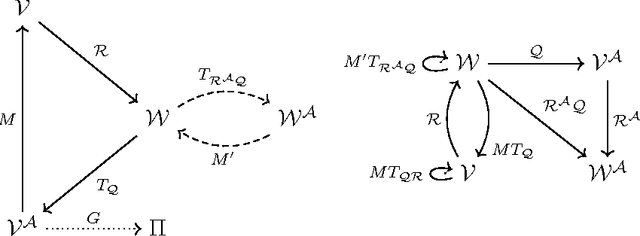
In this paper we study a model-based approach to calculating approximately optimal policies in Markovian Decision Processes. In particular, we derive novel bounds on the loss of using a policy derived from a factored linear model, a class of models which generalize numerous previous models out of those that come with strong computational guarantees. For the first time in the literature, we derive performance bounds for model-based techniques where the model inaccuracy is measured in weighted norms. Moreover, our bounds show a decreased sensitivity to the discount factor and, unlike similar bounds derived for other approaches, they are insensitive to measure mismatch. Similarly to previous works, our proofs are also based on contraction arguments, but with the main differences that we use carefully constructed norms building on Banach lattices, and the contraction property is only assumed for operators acting on "compressed" spaces, thus weakening previous assumptions, while strengthening previous results.