Entropy, concentration, and learning: a statistical mechanics primer

Artificial intelligence models trained through loss minimization have demonstrated significant success, grounded in principles from fields like information theory and statistical physics. This work explores these established connections through the lens of statistical mechanics, starting from first-principles sample concentration behaviors that underpin AI and machine learning. Our development of statistical mechanics for modeling highlights the key role of exponential families, and quantities of statistics, physics, and information theory.

WILDS: A Benchmark of in-the-Wild Distribution Shifts

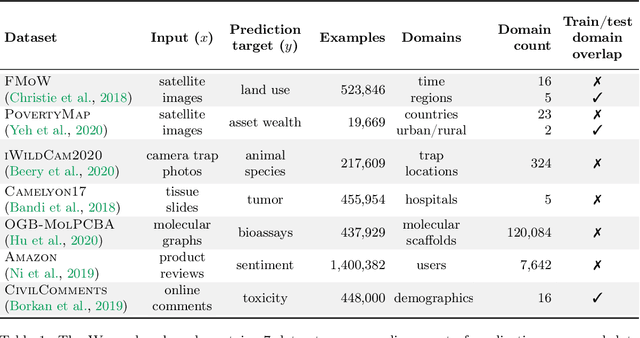
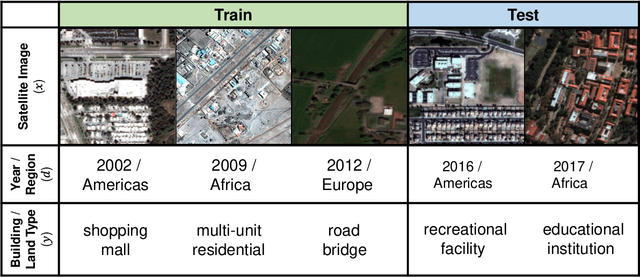
Distribution shifts can cause significant degradation in a broad range of machine learning (ML) systems deployed in the wild. However, many widely-used datasets in the ML community today were not designed for evaluating distribution shifts. These datasets typically have training and test sets drawn from the same distribution, and prior work on retrofitting them with distribution shifts has generally relied on artificial shifts that need not represent the kinds of shifts encountered in the wild. In this paper, we present WILDS, a benchmark of in-the-wild distribution shifts spanning diverse data modalities and applications, from tumor identification to wildlife monitoring to poverty mapping. WILDS builds on top of recent data collection efforts by domain experts in these applications and provides a unified collection of datasets with evaluation metrics and train/test splits that are representative of real-world distribution shifts. These datasets reflect distribution shifts arising from training and testing on different hospitals, cameras, countries, time periods, demographics, molecular scaffolds, etc., all of which cause substantial performance drops in our baseline models. Finally, we survey other applications that would be promising additions to the benchmark but for which we did not manage to find appropriate datasets; we discuss their associated challenges and detail datasets and shifts where we did not see an appreciable performance drop. By unifying datasets from a variety of application areas and making them accessible to the ML community, we hope to encourage the development of general-purpose methods that are anchored to real-world distribution shifts and that work well across different applications and problem settings. Data loaders, default models, and leaderboards are available at https://wilds.stanford.edu.

p-value peeking and estimating extrema

A pervasive issue in statistical hypothesis testing is that the reported $p$-values are biased downward by data "peeking" -- the practice of reporting only progressively extreme values of the test statistic as more data samples are collected. We develop principled mechanisms to estimate such running extrema of test statistics, which directly address the effect of peeking in some general scenarios.

Sharp finite-sample large deviation bounds for independent variables

We show an extension of Sanov's theorem in large deviations theory, controlling the tail probabilities of i.i.d. random variables with matching concentration and anti-concentration bounds. This result applies to samples of any size, and has a short information-theoretic proof using elementary techniques.

Learning transport cost from subset correspondence

Learning to align multiple datasets is an important problem with many applications, and it is especially useful when we need to integrate multiple experiments or correct for confounding. Optimal transport (OT) is a principled approach to align datasets, but a key challenge in applying OT is that we need to specify a transport cost function that accurately captures how the two datasets are related. Reliable cost functions are typically not available and practitioners often resort to using hand-crafted or Euclidean cost even if it may not be appropriate. In this work, we investigate how to learn the cost function using a small amount of side information which is often available. The side information we consider captures subset correspondence---i.e. certain subsets of points in the two data sets are known to be related. For example, we may have some images labeled as cars in both datasets; or we may have a common annotated cell type in single-cell data from two batches. We develop an end-to-end optimizer (OT-SI) that differentiates through the Sinkhorn algorithm and effectively learns the suitable cost function from side information. On systematic experiments in images, marriage-matching and single-cell RNA-seq, our method substantially outperform state-of-the-art benchmarks.

An adaptive nearest neighbor rule for classification

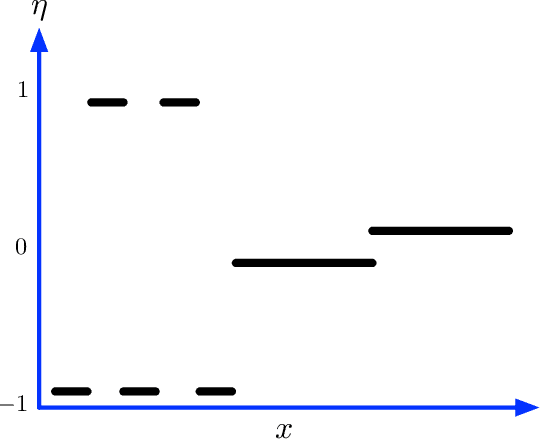
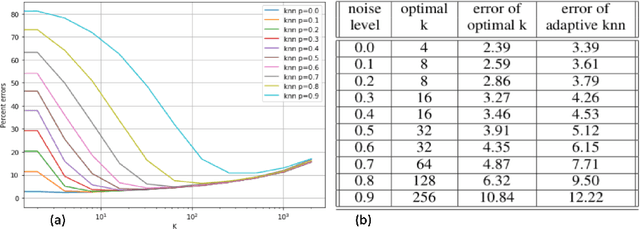
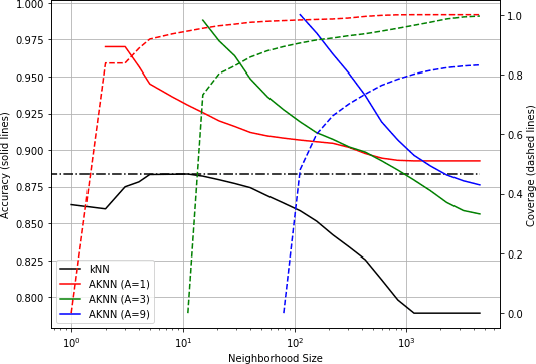
We introduce a variant of the $k$-nearest neighbor classifier in which $k$ is chosen adaptively for each query, rather than supplied as a parameter. The choice of $k$ depends on properties of each neighborhood, and therefore may significantly vary between different points. (For example, the algorithm will use larger $k$ for predicting the labels of points in noisy regions.) We provide theory and experiments that demonstrate that the algorithm performs comparably to, and sometimes better than, $k$-NN with an optimal choice of $k$. In particular, we derive bounds on the convergence rates of our classifier that depend on a local quantity we call the `advantage' which is significantly weaker than the Lipschitz conditions used in previous convergence rate proofs. These generalization bounds hinge on a variant of the seminal Uniform Convergence Theorem due to Vapnik and Chervonenkis; this variant concerns conditional probabilities and may be of independent interest.

Semantically Decomposing the Latent Spaces of Generative Adversarial Networks

We propose a new algorithm for training generative adversarial networks that jointly learns latent codes for both identities (e.g. individual humans) and observations (e.g. specific photographs). By fixing the identity portion of the latent codes, we can generate diverse images of the same subject, and by fixing the observation portion, we can traverse the manifold of subjects while maintaining contingent aspects such as lighting and pose. Our algorithm features a pairwise training scheme in which each sample from the generator consists of two images with a common identity code. Corresponding samples from the real dataset consist of two distinct photographs of the same subject. In order to fool the discriminator, the generator must produce pairs that are photorealistic, distinct, and appear to depict the same individual. We augment both the DCGAN and BEGAN approaches with Siamese discriminators to facilitate pairwise training. Experiments with human judges and an off-the-shelf face verification system demonstrate our algorithm's ability to generate convincing, identity-matched photographs.

Linking Generative Adversarial Learning and Binary Classification

In this note, we point out a basic link between generative adversarial (GA) training and binary classification -- any powerful discriminator essentially computes an (f-)divergence between real and generated samples. The result, repeatedly re-derived in decision theory, has implications for GA Networks (GANs), providing an alternative perspective on training f-GANs by designing the discriminator loss function.

Learning to Abstain from Binary Prediction

A binary classifier capable of abstaining from making a label prediction has two goals in tension: minimizing errors, and avoiding abstaining unnecessarily often. In this work, we exactly characterize the best achievable tradeoff between these two goals in a general semi-supervised setting, given an ensemble of predictors of varying competence as well as unlabeled data on which we wish to predict or abstain. We give an algorithm for learning a classifier in this setting which trades off its errors with abstentions in a minimax optimal manner, is as efficient as linear learning and prediction, and is demonstrably practical. Our analysis extends to a large class of loss functions and other scenarios, including ensembles comprised of specialists that can themselves abstain.

Optimal Binary Autoencoding with Pairwise Correlations

We formulate learning of a binary autoencoder as a biconvex optimization problem which learns from the pairwise correlations between encoded and decoded bits. Among all possible algorithms that use this information, ours finds the autoencoder that reconstructs its inputs with worst-case optimal loss. The optimal decoder is a single layer of artificial neurons, emerging entirely from the minimax loss minimization, and with weights learned by convex optimization. All this is reflected in competitive experimental results, demonstrating that binary autoencoding can be done efficiently by conveying information in pairwise correlations in an optimal fashion.