LEGO-Net: Learning Regular Rearrangements of Objects in Rooms

Humans universally dislike the task of cleaning up a messy room. If machines were to help us with this task, they must understand human criteria for regular arrangements, such as several types of symmetry, co-linearity or co-circularity, spacing uniformity in linear or circular patterns, and further inter-object relationships that relate to style and functionality. Previous approaches for this task relied on human input to explicitly specify goal state, or synthesized scenes from scratch -- but such methods do not address the rearrangement of existing messy scenes without providing a goal state. In this paper, we present LEGO-Net, a data-driven transformer-based iterative method for learning regular rearrangement of objects in messy rooms. LEGO-Net is partly inspired by diffusion models -- it starts with an initial messy state and iteratively "de-noises'' the position and orientation of objects to a regular state while reducing the distance traveled. Given randomly perturbed object positions and orientations in an existing dataset of professionally-arranged scenes, our method is trained to recover a regular re-arrangement. Results demonstrate that our method is able to reliably rearrange room scenes and outperform other methods. We additionally propose a metric for evaluating regularity in room arrangements using number-theoretic machinery.

Canonical Fields: Self-Supervised Learning of Pose-Canonicalized Neural Fields

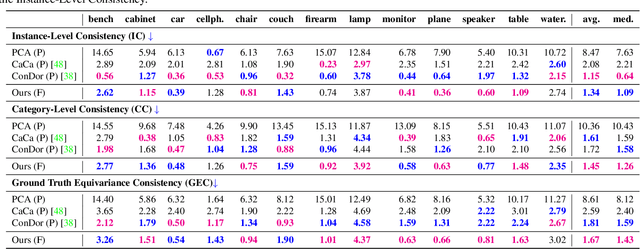
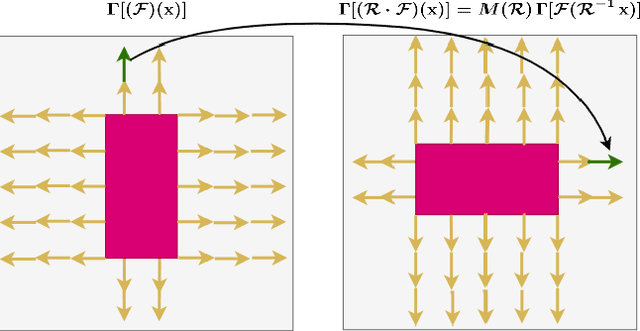
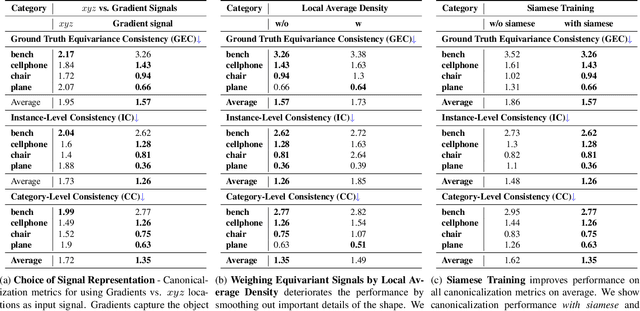
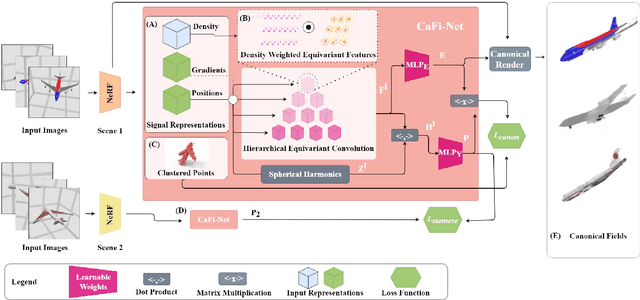
Coordinate-based implicit neural networks, or neural fields, have emerged as useful representations of shape and appearance in 3D computer vision. Despite advances however, it remains challenging to build neural fields for categories of objects without datasets like ShapeNet that provide canonicalized object instances that are consistently aligned for their 3D position and orientation (pose). We present Canonical Field Network (CaFi-Net), a self-supervised method to canonicalize the 3D pose of instances from an object category represented as neural fields, specifically neural radiance fields (NeRFs). CaFi-Net directly learns from continuous and noisy radiance fields using a Siamese network architecture that is designed to extract equivariant field features for category-level canonicalization. During inference, our method takes pre-trained neural radiance fields of novel object instances at arbitrary 3D pose, and estimates a canonical field with consistent 3D pose across the entire category. Extensive experiments on a new dataset of 1300 NeRF models across 13 object categories show that our method matches or exceeds the performance of 3D point cloud-based methods.

Equivalence Between SE(3) Equivariant Networks via Steerable Kernels and Group Convolution

A wide range of techniques have been proposed in recent years for designing neural networks for 3D data that are equivariant under rotation and translation of the input. Most approaches for equivariance under the Euclidean group $\mathrm{SE}(3)$ of rotations and translations fall within one of the two major categories. The first category consists of methods that use $\mathrm{SE}(3)$-convolution which generalizes classical $\mathbb{R}^3$-convolution on signals over $\mathrm{SE}(3)$. Alternatively, it is possible to use \textit{steerable convolution} which achieves $\mathrm{SE}(3)$-equivariance by imposing constraints on $\mathbb{R}^3$-convolution of tensor fields. It is known by specialists in the field that the two approaches are equivalent, with steerable convolution being the Fourier transform of $\mathrm{SE}(3)$ convolution. Unfortunately, these results are not widely known and moreover the exact relations between deep learning architectures built upon these two approaches have not been precisely described in the literature on equivariant deep learning. In this work we provide an in-depth analysis of both methods and their equivalence and relate the two constructions to multiview convolutional networks. Furthermore, we provide theoretical justifications of separability of $\mathrm{SE}(3)$ group convolution, which explain the applicability and success of some recent approaches. Finally, we express different methods using a single coherent formalism and provide explicit formulas that relate the kernels learned by different methods. In this way, our work helps to unify different previously-proposed techniques for achieving roto-translational equivariance, and helps to shed light on both the utility and precise differences between various alternatives. We also derive new TFN non-linearities from our equivalence principle and test them on practical benchmark datasets.

Breaking the Symmetry: Resolving Symmetry Ambiguities in Equivariant Neural Networks

Equivariant networks have been adopted in many 3-D learning areas. Here we identify a fundamental limitation of these networks: their ambiguity to symmetries. Equivariant networks cannot complete symmetry-dependent tasks like segmenting a left-right symmetric object into its left and right sides. We tackle this problem by adding components that resolve symmetry ambiguities while preserving rotational equivariance. We present OAVNN: Orientation Aware Vector Neuron Network, an extension of the Vector Neuron Network. OAVNN is a rotation equivariant network that is robust to planar symmetric inputs. Our network consists of three key components. 1) We introduce an algorithm to calculate symmetry detecting features. 2) We create a symmetry-sensitive orientation aware linear layer. 3) We construct an attention mechanism that relates directional information across points. We evaluate the network using left-right segmentation and find that the network quickly obtains accurate segmentations. We hope this work motivates investigations on the expressivity of equivariant networks on symmetric objects.

ConDor: Self-Supervised Canonicalization of 3D Pose for Partial Shapes

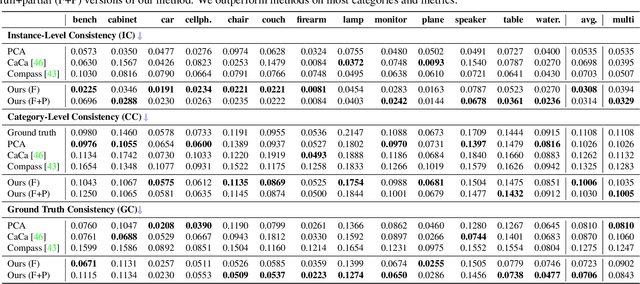
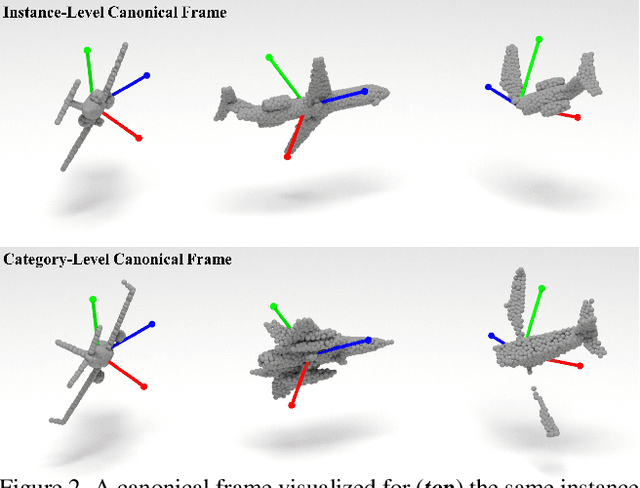
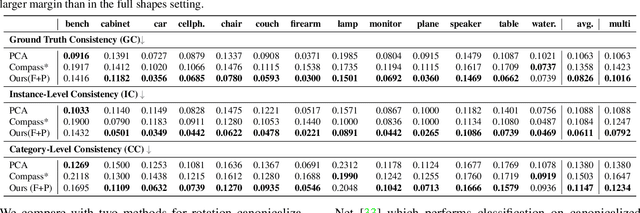
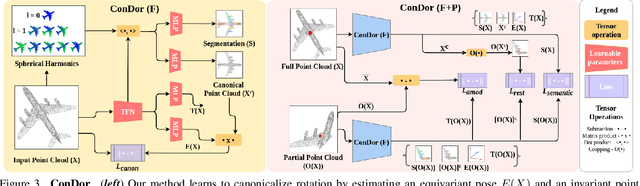
Progress in 3D object understanding has relied on manually canonicalized shape datasets that contain instances with consistent position and orientation (3D pose). This has made it hard to generalize these methods to in-the-wild shapes, eg., from internet model collections or depth sensors. ConDor is a self-supervised method that learns to Canonicalize the 3D orientation and position for full and partial 3D point clouds. We build on top of Tensor Field Networks (TFNs), a class of permutation- and rotation-equivariant, and translation-invariant 3D networks. During inference, our method takes an unseen full or partial 3D point cloud at an arbitrary pose and outputs an equivariant canonical pose. During training, this network uses self-supervision losses to learn the canonical pose from an un-canonicalized collection of full and partial 3D point clouds. ConDor can also learn to consistently co-segment object parts without any supervision. Extensive quantitative results on four new metrics show that our approach outperforms existing methods while enabling new applications such as operation on depth images and annotation transfer.

Vector Neurons: A General Framework for SO-Equivariant Networks

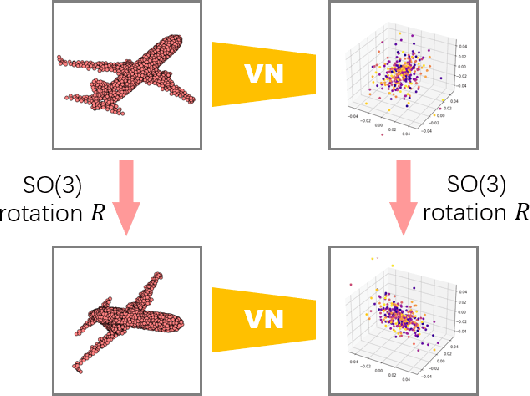
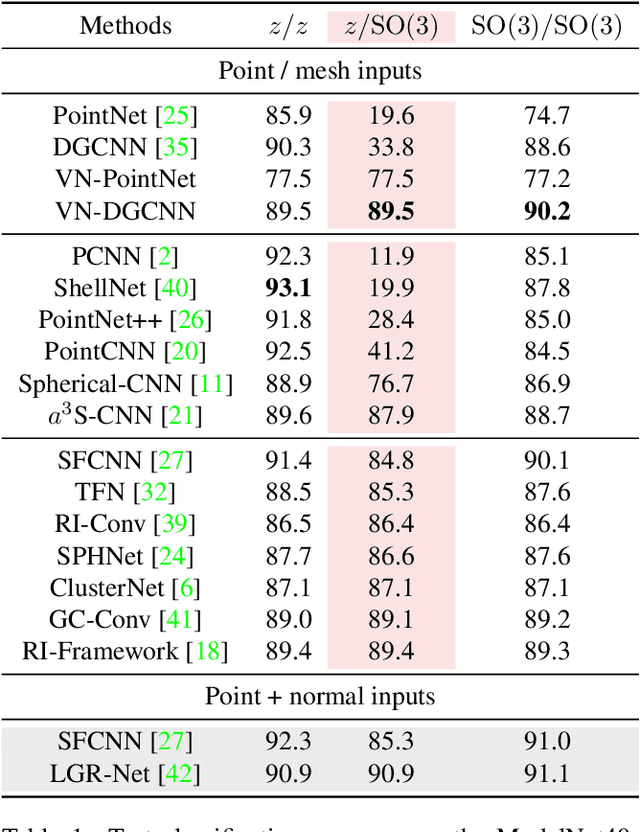
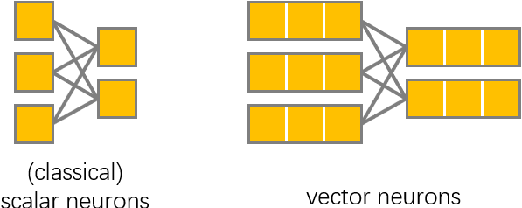
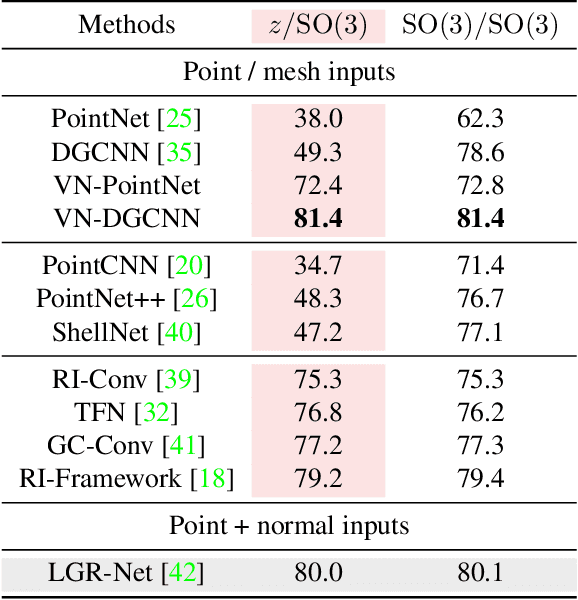
Invariance and equivariance to the rotation group have been widely discussed in the 3D deep learning community for pointclouds. Yet most proposed methods either use complex mathematical tools that may limit their accessibility, or are tied to specific input data types and network architectures. In this paper, we introduce a general framework built on top of what we call Vector Neuron representations for creating SO(3)-equivariant neural networks for pointcloud processing. Extending neurons from 1D scalars to 3D vectors, our vector neurons enable a simple mapping of SO(3) actions to latent spaces thereby providing a framework for building equivariance in common neural operations -- including linear layers, non-linearities, pooling, and normalizations. Due to their simplicity, vector neurons are versatile and, as we demonstrate, can be incorporated into diverse network architecture backbones, allowing them to process geometry inputs in arbitrary poses. Despite its simplicity, our method performs comparably well in accuracy and generalization with other more complex and specialized state-of-the-art methods on classification and segmentation tasks. We also show for the first time a rotation equivariant reconstruction network.

Effective Rotation-invariant Point CNN with Spherical Harmonics kernels

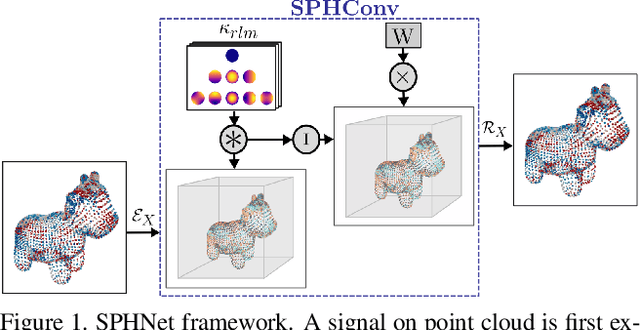
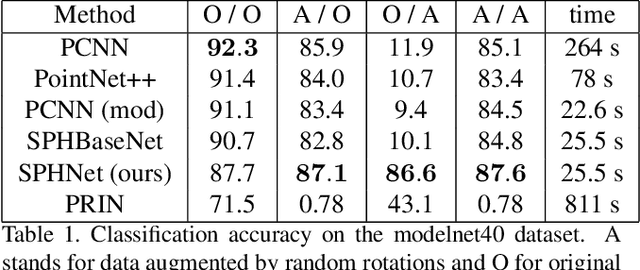
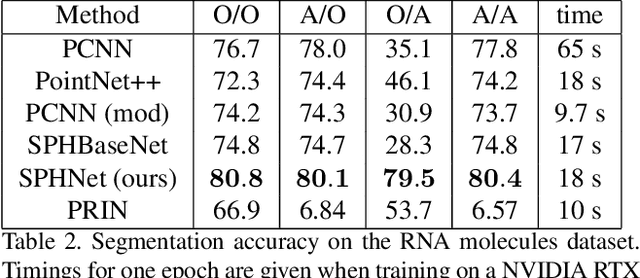
We present a novel rotation invariant architecture operating directly on point cloud data. We demonstrate how rotation invariance can be injected into a recently proposed point-based PCNN architecture, at all layers of the network, achieving invariance to both global shape transformations, and to local rotations on the level of patches or parts, useful when dealing with non-rigid objects. We achieve this by employing a spherical harmonics based kernel at different layers of the network, which is guaranteed to be invariant to rigid motions. We also introduce a more efficient pooling operation for PCNN using space-partitioning data-structures. This results in a flexible, simple and efficient architecture that achieves accurate results on challenging shape analysis tasks including classification and segmentation, without requiring data-augmentation, typically employed by non-invariant approaches.

Multi-directional Geodesic Neural Networks via Equivariant Convolution

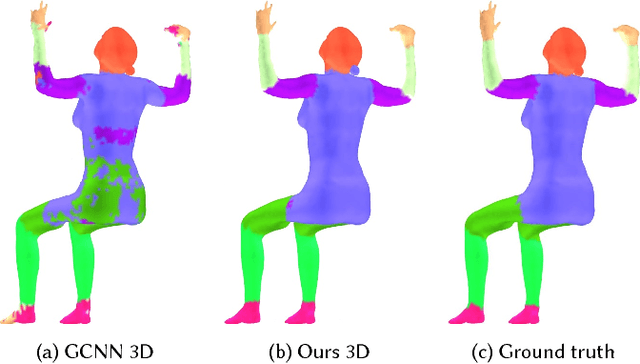
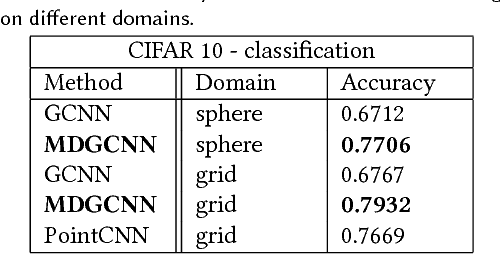
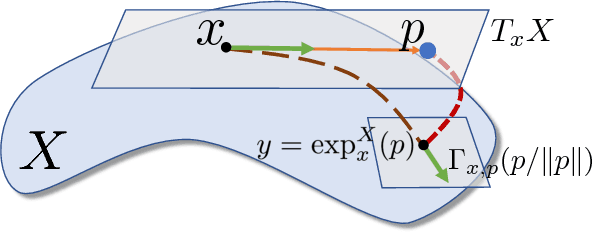
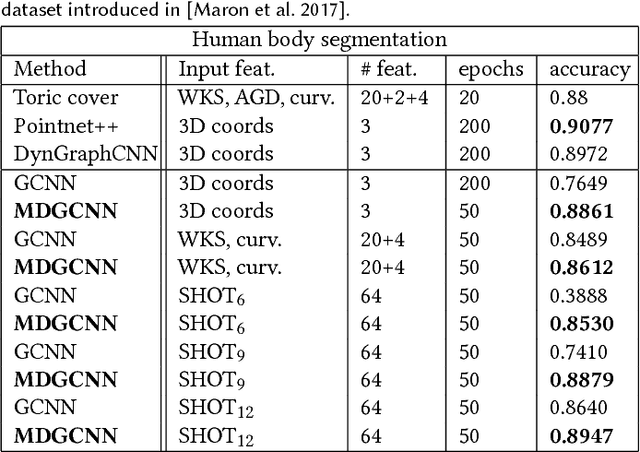
We propose a novel approach for performing convolution of signals on curved surfaces and show its utility in a variety of geometric deep learning applications. Key to our construction is the notion of directional functions defined on the surface, which extend the classic real-valued signals and which can be naturally convolved with with real-valued template functions. As a result, rather than trying to fix a canonical orientation or only keeping the maximal response across all alignments of a 2D template at every point of the surface, as done in previous works, we show how information across all rotations can be kept across different layers of the neural network. Our construction, which we call multi-directional geodesic convolution, or directional convolution for short, allows, in particular, to propagate and relate directional information across layers and thus different regions on the shape. We first define directional convolution in the continuous setting, prove its key properties and then show how it can be implemented in practice, for shapes represented as triangle meshes. We evaluate directional convolution in a wide variety of learning scenarios ranging from classification of signals on surfaces, to shape segmentation and shape matching, where we show a significant improvement over several baselines.