Sequence graphs realizations and ambiguity in language models

Several popular language models represent local contexts in an input text as bags of words. Such representations are naturally encoded by a sequence graph whose vertices are the distinct words occurring in x, with edges representing the (ordered) co-occurrence of two words within a sliding window of size w. However, this compressed representation is not generally bijective, and may introduce some degree of ambiguity. Some sequence graphs may admit several realizations as a sequence, while others may not admit any realization. In this paper, we study the realizability and ambiguity of sequence graphs from a combinatorial and computational point of view. We consider the existence and enumeration of realizations of a sequence graph under multiple settings: window size w, presence/absence of graph orientation, and presence/absence of weights (multiplicities). When w = 2, we provide polynomial time algorithms for realizability and enumeration in all cases except the undirected/weighted setting, where we show the #P-hardness of enumeration. For a window of size at least 3, we prove hardness of all variants, even when w is considered as a constant, with the notable exception of the undirected/unweighted case for which we propose an XP algorithms for both (realizability and enumeration) problems, tight due to a corresponding W[1]-hardness result. We conclude with an integer program formulation to solve the realizability problem, and with dynamic programming to solve the enumeration problem. This work leaves open the membership to NP for both problems, a non-trivial question due to the existence of minimum realizations having exponential size on the instance encoding.

Effective Rotation-invariant Point CNN with Spherical Harmonics kernels

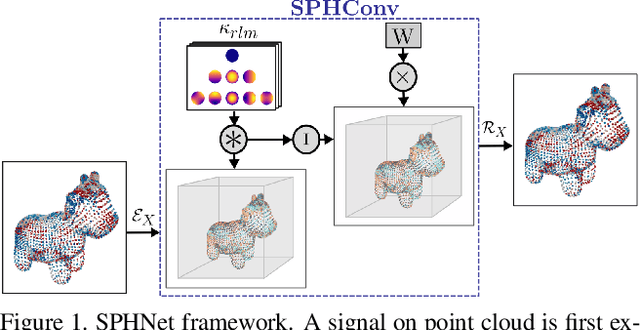
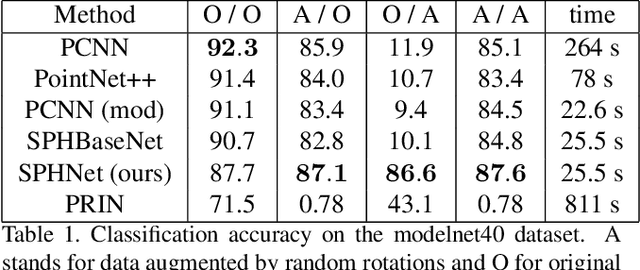
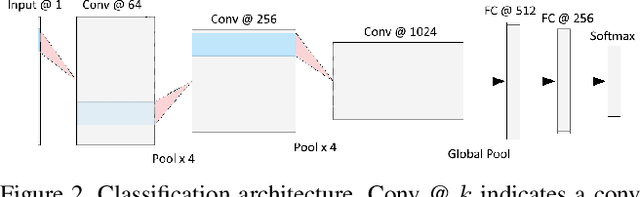
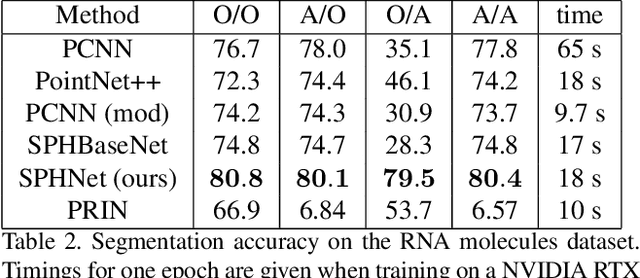
We present a novel rotation invariant architecture operating directly on point cloud data. We demonstrate how rotation invariance can be injected into a recently proposed point-based PCNN architecture, at all layers of the network, achieving invariance to both global shape transformations, and to local rotations on the level of patches or parts, useful when dealing with non-rigid objects. We achieve this by employing a spherical harmonics based kernel at different layers of the network, which is guaranteed to be invariant to rigid motions. We also introduce a more efficient pooling operation for PCNN using space-partitioning data-structures. This results in a flexible, simple and efficient architecture that achieves accurate results on challenging shape analysis tasks including classification and segmentation, without requiring data-augmentation, typically employed by non-invariant approaches.

Rule-weighted and terminal-weighted context-free grammars have identical expressivity

Two formalisms, both based on context-free grammars, have recently been proposed as a basis for a non-uniform random generation of combinatorial objects. The former, introduced by Denise et al, associates weights with letters, while the latter, recently explored by Weinberg et al in the context of random generation, associates weights to transitions. In this short note, we use a simple modification of the Greibach Normal Form transformation algorithm, due to Blum and Koch, to show the equivalent expressivities, in term of their induced distributions, of these two formalisms.