Heavy-tailed Streaming Statistical Estimation

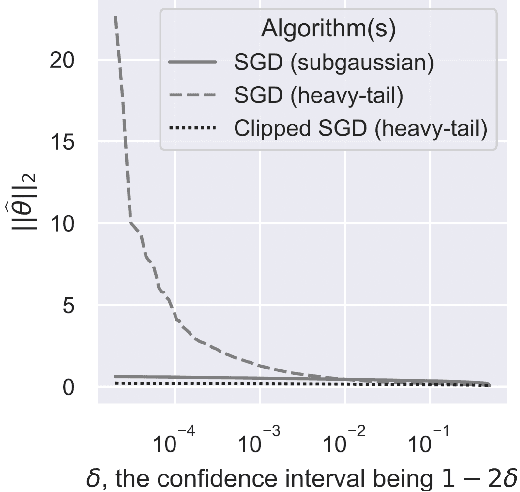
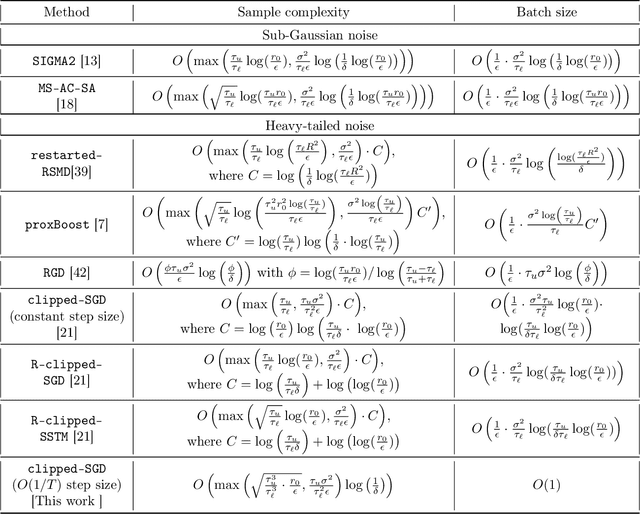
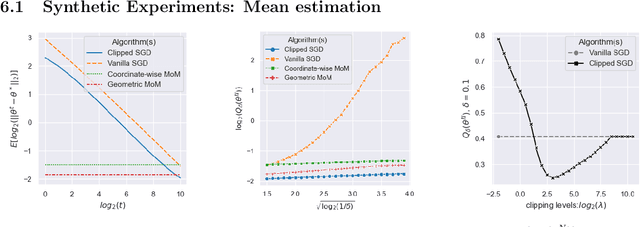
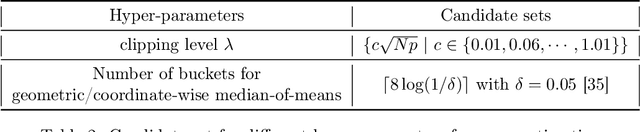
We consider the task of heavy-tailed statistical estimation given streaming $p$-dimensional samples. This could also be viewed as stochastic optimization under heavy-tailed distributions, with an additional $O(p)$ space complexity constraint. We design a clipped stochastic gradient descent algorithm and provide an improved analysis, under a more nuanced condition on the noise of the stochastic gradients, which we show is critical when analyzing stochastic optimization problems arising from general statistical estimation problems. Our results guarantee convergence not just in expectation but with exponential concentration, and moreover does so using $O(1)$ batch size. We provide consequences of our results for mean estimation and linear regression. Finally, we provide empirical corroboration of our results and algorithms via synthetic experiments for mean estimation and linear regression.

On Proximal Policy Optimization's Heavy-tailed Gradients

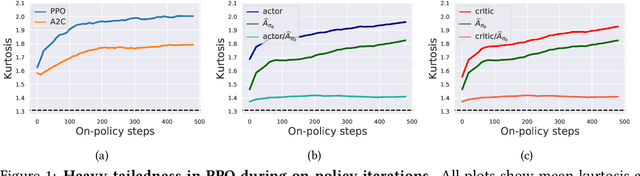
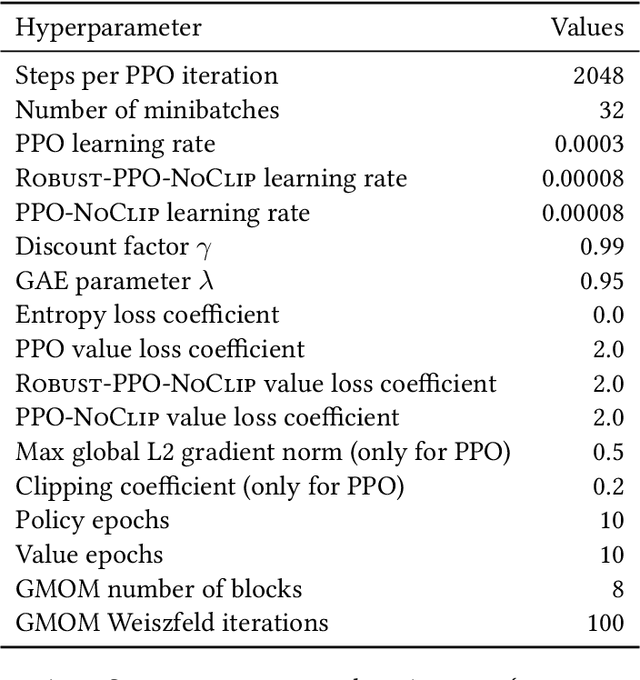
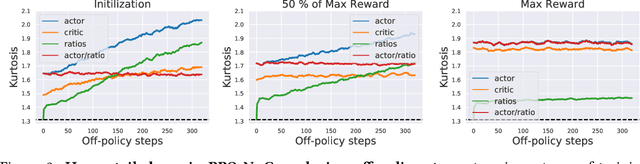
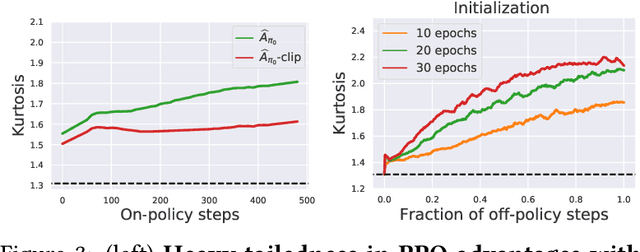
Modern policy gradient algorithms, notably Proximal Policy Optimization (PPO), rely on an arsenal of heuristics, including loss clipping and gradient clipping, to ensure successful learning. These heuristics are reminiscent of techniques from robust statistics, commonly used for estimation in outlier-rich ("heavy-tailed") regimes. In this paper, we present a detailed empirical study to characterize the heavy-tailed nature of the gradients of the PPO surrogate reward function. We demonstrate that the gradients, especially for the actor network, exhibit pronounced heavy-tailedness and that it increases as the agent's policy diverges from the behavioral policy (i.e., as the agent goes further off policy). Further examination implicates the likelihood ratios and advantages in the surrogate reward as the main sources of the observed heavy-tailedness. We then highlight issues arising due to the heavy-tailed nature of the gradients. In this light, we study the effects of the standard PPO clipping heuristics, demonstrating that these tricks primarily serve to offset heavy-tailedness in gradients. Thus motivated, we propose incorporating GMOM, a high-dimensional robust estimator, into PPO as a substitute for three clipping tricks. Despite requiring less hyperparameter tuning, our method matches the performance of PPO (with all heuristics enabled) on a battery of MuJoCo continuous control tasks.

Robust Linear Regression: Optimal Rates in Polynomial Time

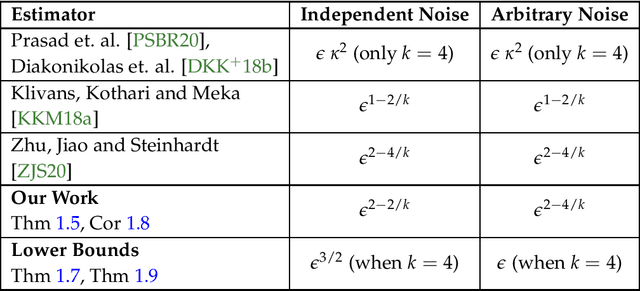
We obtain a robust and computationally efficient estimator for Linear Regression that achieves statistically optimal convergence rate under mild distributional assumptions. Concretely, we assume our data is drawn from a $k$-hypercontractive distribution and an $\epsilon$-fraction is adversarially corrupted. We then describe an estimator that converges to the optimal least-squares minimizer for the true distribution at a rate proportional to $\epsilon^{2-2/k}$, when the noise is independent of the covariates. We note that no such estimator was known prior to our work, even with access to unbounded computation. The rate we achieve is information-theoretically optimal and thus we resolve the main open question in Klivans, Kothari and Meka [COLT'18]. Our key insight is to identify an analytic condition relating the distribution over the noise and covariates that completely characterizes the rate of convergence, regardless of the noise model. In particular, we show that when the moments of the noise and covariates are negatively-correlated, we obtain the same rate as independent noise. Further, when the condition is not satisfied, we obtain a rate proportional to $\epsilon^{2-4/k}$, and again match the information-theoretic lower bound. Our central technical contribution is to algorithmically exploit independence of random variables in the "sum-of-squares" framework by formulating it as a polynomial identity.

Learning Minimax Estimators via Online Learning

We consider the problem of designing minimax estimators for estimating the parameters of a probability distribution. Unlike classical approaches such as the MLE and minimum distance estimators, we consider an algorithmic approach for constructing such estimators. We view the problem of designing minimax estimators as finding a mixed strategy Nash equilibrium of a zero-sum game. By leveraging recent results in online learning with non-convex losses, we provide a general algorithm for finding a mixed-strategy Nash equilibrium of general non-convex non-concave zero-sum games. Our algorithm requires access to two subroutines: (a) one which outputs a Bayes estimator corresponding to a given prior probability distribution, and (b) one which computes the worst-case risk of any given estimator. Given access to these two subroutines, we show that our algorithm outputs both a minimax estimator and a least favorable prior. To demonstrate the power of this approach, we use it to construct provably minimax estimators for classical problems such as estimation in the finite Gaussian sequence model, and linear regression.

A Unified Approach to Robust Mean Estimation

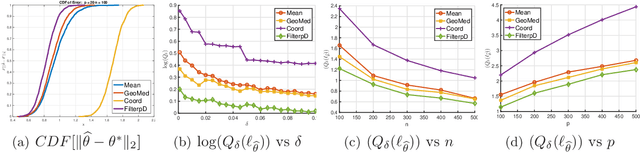
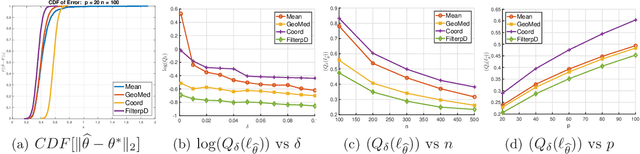
In this paper, we develop connections between two seemingly disparate, but central, models in robust statistics: Huber's epsilon-contamination model and the heavy-tailed noise model. We provide conditions under which this connection provides near-statistically-optimal estimators. Building on this connection, we provide a simple variant of recent computationally-efficient algorithms for mean estimation in Huber's model, which given our connection entails that the same efficient sample-pruning based estimators is simultaneously robust to heavy-tailed noise and Huber contamination. Furthermore, we complement our efficient algorithms with statistically-optimal albeit computationally intractable estimators, which are simultaneously optimally robust in both models. We study the empirical performance of our proposed estimators on synthetic datasets, and find that our methods convincingly outperform a variety of practical baselines.

On Adversarial Risk and Training

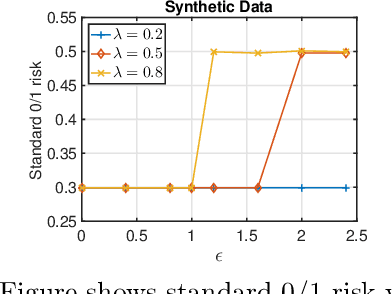
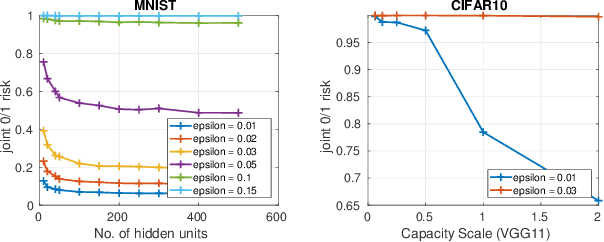
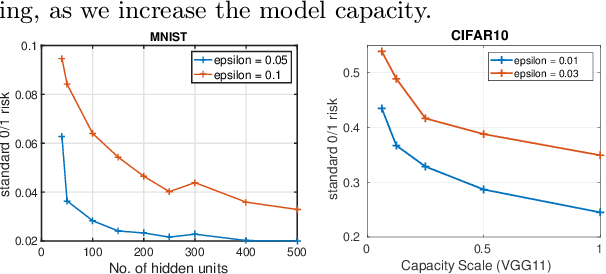
In this work we formally define the notions of adversarial perturbations, adversarial risk and adversarial training and analyze their properties. Our analysis provides several interesting insights into adversarial risk, adversarial training, and their relation to the classification risk, "traditional" training. We also show that adversarial training can result in models with better classification accuracy and can result in better explainable models than traditional training. Although adversarial training is computationally expensive, our results and insights suggest that one should prefer adversarial training over traditional risk minimization for learning complex models from data.

Robust Estimation via Robust Gradient Estimation

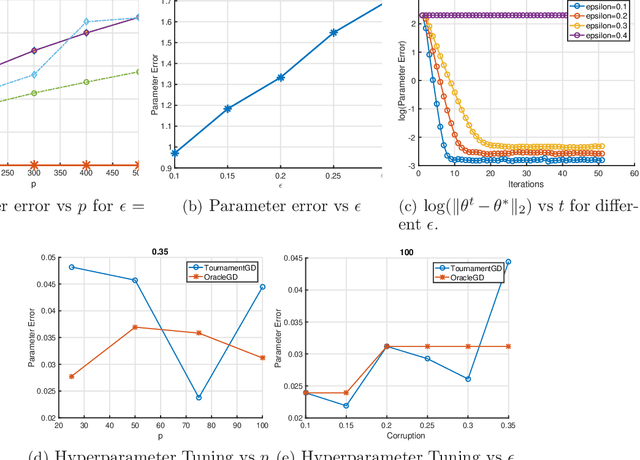
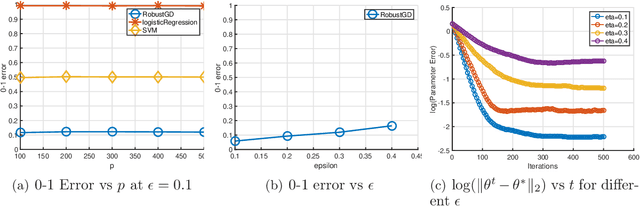
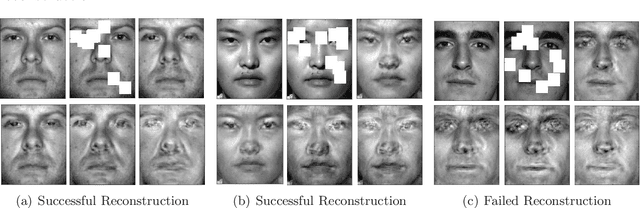
We provide a new computationally-efficient class of estimators for risk minimization. We show that these estimators are robust for general statistical models: in the classical Huber epsilon-contamination model and in heavy-tailed settings. Our workhorse is a novel robust variant of gradient descent, and we provide conditions under which our gradient descent variant provides accurate estimators in a general convex risk minimization problem. We provide specific consequences of our theory for linear regression, logistic regression and for estimation of the canonical parameters in an exponential family. These results provide some of the first computationally tractable and provably robust estimators for these canonical statistical models. Finally, we study the empirical performance of our proposed methods on synthetic and real datasets, and find that our methods convincingly outperform a variety of baselines.

Submodular meets Structured: Finding Diverse Subsets in Exponentially-Large Structured Item Sets

To cope with the high level of ambiguity faced in domains such as Computer Vision or Natural Language processing, robust prediction methods often search for a diverse set of high-quality candidate solutions or proposals. In structured prediction problems, this becomes a daunting task, as the solution space (image labelings, sentence parses, etc.) is exponentially large. We study greedy algorithms for finding a diverse subset of solutions in structured-output spaces by drawing new connections between submodular functions over combinatorial item sets and High-Order Potentials (HOPs) studied for graphical models. Specifically, we show via examples that when marginal gains of submodular diversity functions allow structured representations, this enables efficient (sub-linear time) approximate maximization by reducing the greedy augmentation step to inference in a factor graph with appropriately constructed HOPs. We discuss benefits, tradeoffs, and show that our constructions lead to significantly better proposals.