Robust Linear Regression: Optimal Rates in Polynomial Time
Paper and Code
Jul 16, 2020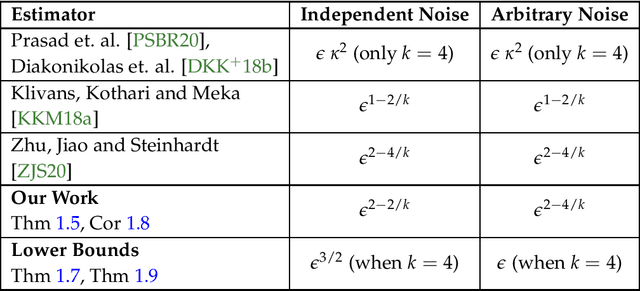
We obtain a robust and computationally efficient estimator for Linear Regression that achieves statistically optimal convergence rate under mild distributional assumptions. Concretely, we assume our data is drawn from a $k$-hypercontractive distribution and an $\epsilon$-fraction is adversarially corrupted. We then describe an estimator that converges to the optimal least-squares minimizer for the true distribution at a rate proportional to $\epsilon^{2-2/k}$, when the noise is independent of the covariates. We note that no such estimator was known prior to our work, even with access to unbounded computation. The rate we achieve is information-theoretically optimal and thus we resolve the main open question in Klivans, Kothari and Meka [COLT'18]. Our key insight is to identify an analytic condition relating the distribution over the noise and covariates that completely characterizes the rate of convergence, regardless of the noise model. In particular, we show that when the moments of the noise and covariates are negatively-correlated, we obtain the same rate as independent noise. Further, when the condition is not satisfied, we obtain a rate proportional to $\epsilon^{2-4/k}$, and again match the information-theoretic lower bound. Our central technical contribution is to algorithmically exploit independence of random variables in the "sum-of-squares" framework by formulating it as a polynomial identity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge