Robust Estimation via Robust Gradient Estimation
Paper and Code
Apr 20, 2018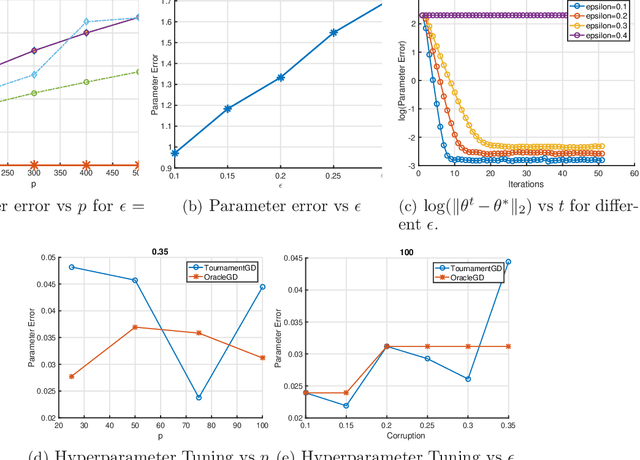

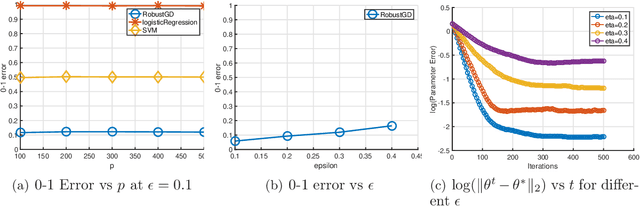
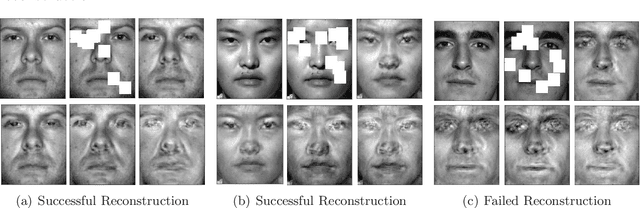
We provide a new computationally-efficient class of estimators for risk minimization. We show that these estimators are robust for general statistical models: in the classical Huber epsilon-contamination model and in heavy-tailed settings. Our workhorse is a novel robust variant of gradient descent, and we provide conditions under which our gradient descent variant provides accurate estimators in a general convex risk minimization problem. We provide specific consequences of our theory for linear regression, logistic regression and for estimation of the canonical parameters in an exponential family. These results provide some of the first computationally tractable and provably robust estimators for these canonical statistical models. Finally, we study the empirical performance of our proposed methods on synthetic and real datasets, and find that our methods convincingly outperform a variety of baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge