A Unified Approach to Robust Mean Estimation
Paper and Code
Jul 01, 2019
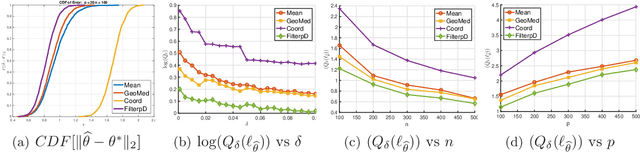
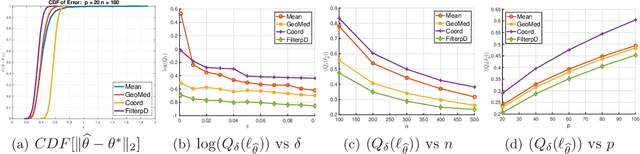
In this paper, we develop connections between two seemingly disparate, but central, models in robust statistics: Huber's epsilon-contamination model and the heavy-tailed noise model. We provide conditions under which this connection provides near-statistically-optimal estimators. Building on this connection, we provide a simple variant of recent computationally-efficient algorithms for mean estimation in Huber's model, which given our connection entails that the same efficient sample-pruning based estimators is simultaneously robust to heavy-tailed noise and Huber contamination. Furthermore, we complement our efficient algorithms with statistically-optimal albeit computationally intractable estimators, which are simultaneously optimally robust in both models. We study the empirical performance of our proposed estimators on synthetic datasets, and find that our methods convincingly outperform a variety of practical baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge