Zixiong Wang
HiMat: DiT-based Ultra-High Resolution SVBRDF Generation
Aug 12, 2025
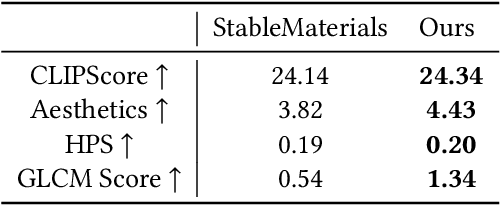

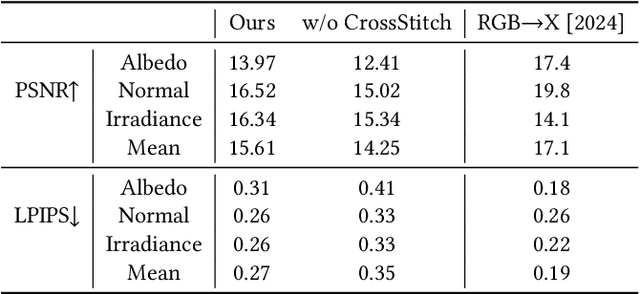
Abstract:Creating highly detailed SVBRDFs is essential for 3D content creation. The rise of high-resolution text-to-image generative models, based on diffusion transformers (DiT), suggests an opportunity to finetune them for this task. However, retargeting the models to produce multiple aligned SVBRDF maps instead of just RGB images, while achieving high efficiency and ensuring consistency across different maps, remains a challenge. In this paper, we introduce HiMat: a memory- and computation-efficient diffusion-based framework capable of generating native 4K-resolution SVBRDFs. A key challenge we address is maintaining consistency across different maps in a lightweight manner, without relying on training new VAEs or significantly altering the DiT backbone (which would damage its prior capabilities). To tackle this, we introduce the CrossStitch module, a lightweight convolutional module that captures inter-map dependencies through localized operations. Its weights are initialized such that the DiT backbone operation is unchanged before finetuning starts. HiMat enables generation with strong structural coherence and high-frequency details. Results with a large set of text prompts demonstrate the effectiveness of our approach for 4K SVBRDF generation. Further experiments suggest generalization to tasks such as intrinsic decomposition.
Membership Inference Attack against Long-Context Large Language Models
Nov 18, 2024Abstract:Recent advances in Large Language Models (LLMs) have enabled them to overcome their context window limitations, and demonstrate exceptional retrieval and reasoning capacities on longer context. Quesion-answering systems augmented with Long-Context Language Models (LCLMs) can automatically search massive external data and incorporate it into their contexts, enabling faithful predictions and reducing issues such as hallucinations and knowledge staleness. Existing studies targeting LCLMs mainly concentrate on addressing the so-called lost-in-the-middle problem or improving the inference effiencicy, leaving their privacy risks largely unexplored. In this paper, we aim to bridge this gap and argue that integrating all information into the long context makes it a repository of sensitive information, which often contains private data such as medical records or personal identities. We further investigate the membership privacy within LCLMs external context, with the aim of determining whether a given document or sequence is included in the LCLMs context. Our basic idea is that if a document lies in the context, it will exhibit a low generation loss or a high degree of semantic similarity to the contents generated by LCLMs. We for the first time propose six membership inference attack (MIA) strategies tailored for LCLMs and conduct extensive experiments on various popular models. Empirical results demonstrate that our attacks can accurately infer membership status in most cases, e.g., 90.66% attack F1-score on Multi-document QA datasets with LongChat-7b-v1.5-32k, highlighting significant risks of membership leakage within LCLMs input contexts. Furthermore, we examine the underlying reasons why LCLMs are susceptible to revealing such membership information.
Neural-Singular-Hessian: Implicit Neural Representation of Unoriented Point Clouds by Enforcing Singular Hessian
Sep 06, 2023Abstract:Neural implicit representation is a promising approach for reconstructing surfaces from point clouds. Existing methods combine various regularization terms, such as the Eikonal and Laplacian energy terms, to enforce the learned neural function to possess the properties of a Signed Distance Function (SDF). However, inferring the actual topology and geometry of the underlying surface from poor-quality unoriented point clouds remains challenging. In accordance with Differential Geometry, the Hessian of the SDF is singular for points within the differential thin-shell space surrounding the surface. Our approach enforces the Hessian of the neural implicit function to have a zero determinant for points near the surface. This technique aligns the gradients for a near-surface point and its on-surface projection point, producing a rough but faithful shape within just a few iterations. By annealing the weight of the singular-Hessian term, our approach ultimately produces a high-fidelity reconstruction result. Extensive experimental results demonstrate that our approach effectively suppresses ghost geometry and recovers details from unoriented point clouds with better expressiveness than existing fitting-based methods.
Mesh-MLP: An all-MLP Architecture for Mesh Classification and Semantic Segmentation
Jun 08, 2023



Abstract:With the rapid development of geometric deep learning techniques, many mesh-based convolutional operators have been proposed to bridge irregular mesh structures and popular backbone networks. In this paper, we show that while convolutions are helpful, a simple architecture based exclusively on multi-layer perceptrons (MLPs) is competent enough to deal with mesh classification and semantic segmentation. Our new network architecture, named Mesh-MLP, takes mesh vertices equipped with the heat kernel signature (HKS) and dihedral angles as the input, replaces the convolution module of a ResNet with Multi-layer Perceptron (MLP), and utilizes layer normalization (LN) to perform the normalization of the layers. The all-MLP architecture operates in an end-to-end fashion and does not include a pooling module. Extensive experimental results on the mesh classification/segmentation tasks validate the effectiveness of the all-MLP architecture.
Laplacian2Mesh: Laplacian-Based Mesh Understanding
Feb 01, 2022Abstract:Geometric deep learning has sparked a rising interest in computer graphics to perform shape understanding tasks, such as shape classification and semantic segmentation on three-dimensional (3D) geometric surfaces. Previous works explored the significant direction by defining the operations of convolution and pooling on triangle meshes, but most methods explicitly utilized the graph connection structure of the mesh. Motivated by the geometric spectral surface reconstruction theory, we introduce a novel and flexible convolutional neural network (CNN) model, called Laplacian2Mesh, for 3D triangle mesh, which maps the features of mesh in the Euclidean space to the multi-dimensional Laplacian-Beltrami space, which is similar to the multi-resolution input in 2D CNN. Mesh pooling is applied to expand the receptive field of the network by the multi-space transformation of Laplacian which retains the surface topology, and channel self-attention convolutions are applied in the new space. Since implicitly using the intrinsic geodesic connections of the mesh through the adjacency matrix, we do not consider the number of the neighbors of the vertices, thereby mesh data with different numbers of vertices can be input. Experiments on various learning tasks applied to 3D meshes demonstrate the effectiveness and efficiency of Laplacian2Mesh.
Neural-IMLS: Learning Implicit Moving Least-Squares for Surface Reconstruction from Unoriented Point clouds
Sep 09, 2021



Abstract:Surface reconstruction from noisy, non-uniformly, and unoriented point clouds is a fascinating yet difficult problem in computer vision and computer graphics. In this paper, we propose Neural-IMLS, a novel approach that learning noise-resistant signed distance function (SDF) for reconstruction. Instead of explicitly learning priors with the ground-truth signed distance values, our method learns the SDF from raw point clouds directly in a self-supervised fashion by minimizing the loss between the couple of SDFs, one obtained by the implicit moving least-square function (IMLS) and the other by our network. Finally, a watertight and smooth 2-manifold triangle mesh is yielded by running Marching Cubes. We conduct extensive experiments on various benchmarks to demonstrate the performance of Neural-IMLS, especially for point clouds with noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge