Zijin Wu
Dual-Camera All-in-Focus Neural Radiance Fields
Apr 23, 2025Abstract:We present the first framework capable of synthesizing the all-in-focus neural radiance field (NeRF) from inputs without manual refocusing. Without refocusing, the camera will automatically focus on the fixed object for all views, and current NeRF methods typically using one camera fail due to the consistent defocus blur and a lack of sharp reference. To restore the all-in-focus NeRF, we introduce the dual-camera from smartphones, where the ultra-wide camera has a wider depth-of-field (DoF) and the main camera possesses a higher resolution. The dual camera pair saves the high-fidelity details from the main camera and uses the ultra-wide camera's deep DoF as reference for all-in-focus restoration. To this end, we first implement spatial warping and color matching to align the dual camera, followed by a defocus-aware fusion module with learnable defocus parameters to predict a defocus map and fuse the aligned camera pair. We also build a multi-view dataset that includes image pairs of the main and ultra-wide cameras in a smartphone. Extensive experiments on this dataset verify that our solution, termed DC-NeRF, can produce high-quality all-in-focus novel views and compares favorably against strong baselines quantitatively and qualitatively. We further show DoF applications of DC-NeRF with adjustable blur intensity and focal plane, including refocusing and split diopter.
Defocus to focus: Photo-realistic bokeh rendering by fusing defocus and radiance priors
Jun 07, 2023



Abstract:We consider the problem of realistic bokeh rendering from a single all-in-focus image. Bokeh rendering mimics aesthetic shallow depth-of-field (DoF) in professional photography, but these visual effects generated by existing methods suffer from simple flat background blur and blurred in-focus regions, giving rise to unrealistic rendered results. In this work, we argue that realistic bokeh rendering should (i) model depth relations and distinguish in-focus regions, (ii) sustain sharp in-focus regions, and (iii) render physically accurate Circle of Confusion (CoC). To this end, we present a Defocus to Focus (D2F) framework to learn realistic bokeh rendering by fusing defocus priors with the all-in-focus image and by implementing radiance priors in layered fusion. Since no depth map is provided, we introduce defocus hallucination to integrate depth by learning to focus. The predicted defocus map implies the blur amount of bokeh and is used to guide weighted layered rendering. In layered rendering, we fuse images blurred by different kernels based on the defocus map. To increase the reality of the bokeh, we adopt radiance virtualization to simulate scene radiance. The scene radiance used in weighted layered rendering reassigns weights in the soft disk kernel to produce the CoC. To ensure the sharpness of in-focus regions, we propose to fuse upsampled bokeh images and original images. We predict the initial fusion mask from our defocus map and refine the mask with a deep network. We evaluate our model on a large-scale bokeh dataset. Extensive experiments show that our approach is capable of rendering visually pleasing bokeh effects in complex scenes. In particular, our solution receives the runner-up award in the AIM 2020 Rendering Realistic Bokeh Challenge.
* Published at Information Fusion 2023 https://www.sciencedirect.com/science/article/pii/S1566253522001221
DoF-NeRF: Depth-of-Field Meets Neural Radiance Fields
Aug 01, 2022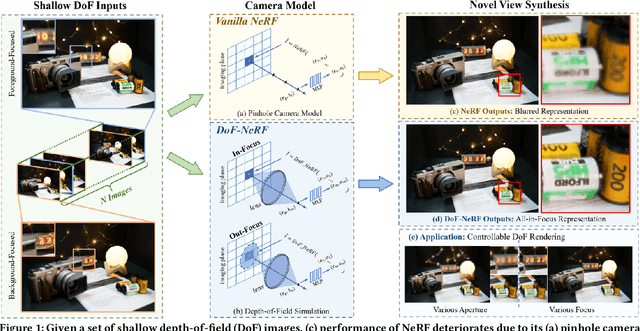
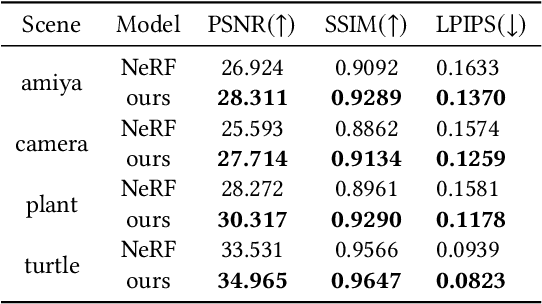
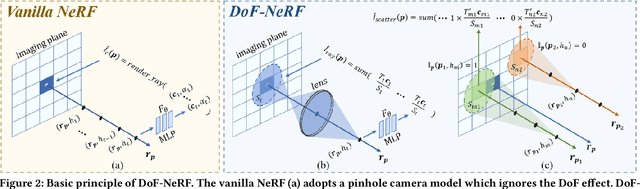
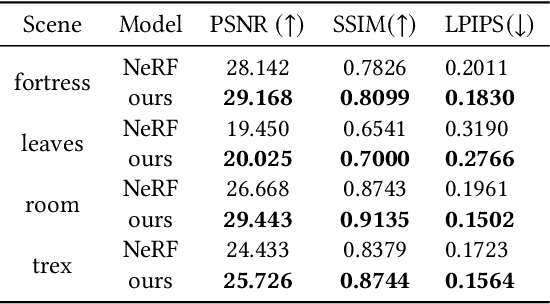
Abstract:Neural Radiance Field (NeRF) and its variants have exhibited great success on representing 3D scenes and synthesizing photo-realistic novel views. However, they are generally based on the pinhole camera model and assume all-in-focus inputs. This limits their applicability as images captured from the real world often have finite depth-of-field (DoF). To mitigate this issue, we introduce DoF-NeRF, a novel neural rendering approach that can deal with shallow DoF inputs and can simulate DoF effect. In particular, it extends NeRF to simulate the aperture of lens following the principles of geometric optics. Such a physical guarantee allows DoF-NeRF to operate views with different focus configurations. Benefiting from explicit aperture modeling, DoF-NeRF also enables direct manipulation of DoF effect by adjusting virtual aperture and focus parameters. It is plug-and-play and can be inserted into NeRF-based frameworks. Experiments on synthetic and real-world datasets show that, DoF-NeRF not only performs comparably with NeRF in the all-in-focus setting, but also can synthesize all-in-focus novel views conditioned on shallow DoF inputs. An interesting application of DoF-NeRF to DoF rendering is also demonstrated. The source code will be made available at https://github.com/zijinwuzijin/DoF-NeRF.
AIM 2020 Challenge on Rendering Realistic Bokeh
Nov 10, 2020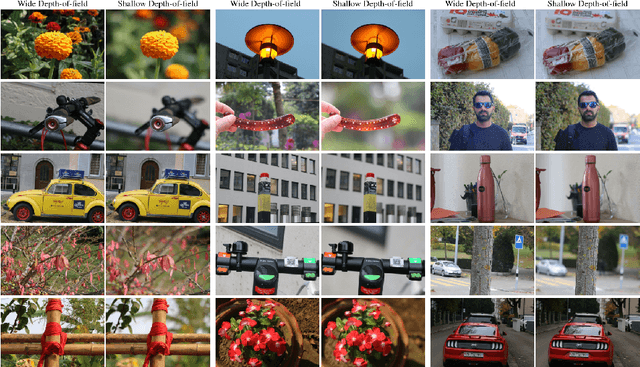


Abstract:This paper reviews the second AIM realistic bokeh effect rendering challenge and provides the description of the proposed solutions and results. The participating teams were solving a real-world bokeh simulation problem, where the goal was to learn a realistic shallow focus technique using a large-scale EBB! bokeh dataset consisting of 5K shallow / wide depth-of-field image pairs captured using the Canon 7D DSLR camera. The participants had to render bokeh effect based on only one single frame without any additional data from other cameras or sensors. The target metric used in this challenge combined the runtime and the perceptual quality of the solutions measured in the user study. To ensure the efficiency of the submitted models, we measured their runtime on standard desktop CPUs as well as were running the models on smartphone GPUs. The proposed solutions significantly improved the baseline results, defining the state-of-the-art for practical bokeh effect rendering problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge