SheafAlign: A Sheaf-theoretic Framework for Decentralized Multimodal Alignment

Conventional multimodal alignment methods assume mutual redundancy across all modalities, an assumption that fails in real-world distributed scenarios. We propose SheafAlign, a sheaf-theoretic framework for decentralized multimodal alignment that replaces single-space alignment with multiple comparison spaces. This approach models pairwise modality relations through sheaf structures and leverages decentralized contrastive learning-based objectives for training. SheafAlign overcomes the limitations of prior methods by not requiring mutual redundancy among all modalities, preserving both shared and unique information. Experiments on multimodal sensing datasets show superior zero-shot generalization, cross-modal alignment, and robustness to missing modalities, with 50\% lower communication cost than state-of-the-art baselines.

Active Inference Framework for Closed-Loop Sensing, Communication, and Control in UAV Systems

Integrated sensing and communication (ISAC) is a core technology for 6G, and its application to closed-loop sensing, communication, and control (SCC) enables various services. Existing SCC solutions often treat sensing and control separately, leading to suboptimal performance and resource usage. In this work, we introduce the active inference framework (AIF) into SCC-enabled unmanned aerial vehicle (UAV) systems for joint state estimation, control, and sensing resource allocation. By formulating a unified generative model, the problem reduces to minimizing variational free energy for inference and expected free energy for action planning. Simulation results show that both control cost and sensing cost are reduced relative to baselines.

Distributed Learning over Networks with Graph-Attention-Based Personalization

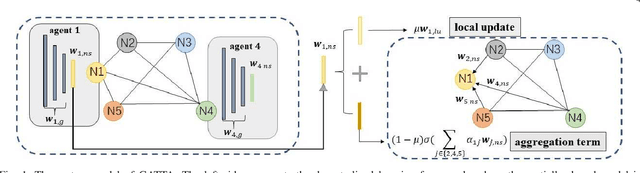
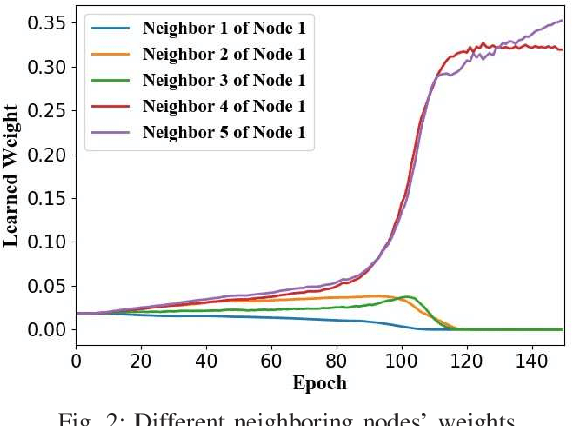
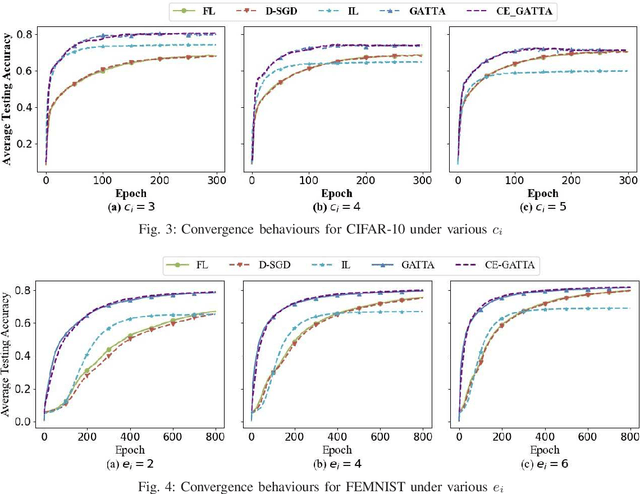
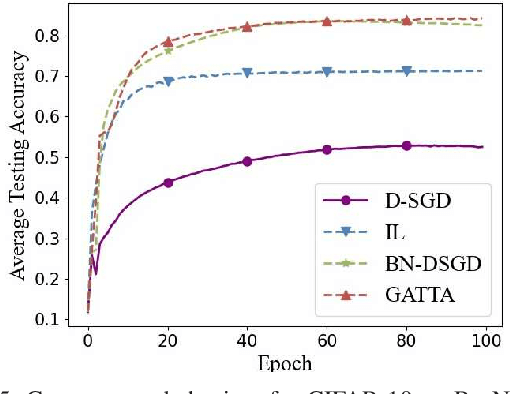
In conventional distributed learning over a network, multiple agents collaboratively build a common machine learning model. However, due to the underlying non-i.i.d. data distribution among agents, the unified learning model becomes inefficient for each agent to process its locally accessible data. To address this problem, we propose a graph-attention-based personalized training algorithm (GATTA) for distributed deep learning. The GATTA enables each agent to train its local personalized model while exploiting its correlation with neighboring nodes and utilizing their useful information for aggregation. In particular, the personalized model in each agent is composed of a global part and a node-specific part. By treating each agent as one node in a graph and the node-specific parameters as its features, the benefits of the graph attention mechanism can be inherited. Namely, instead of aggregation based on averaging, it learns the specific weights for different neighboring nodes without requiring prior knowledge about the graph structure or the neighboring nodes' data distribution. Furthermore, relying on the weight-learning procedure, we develop a communication-efficient GATTA by skipping the transmission of information with small aggregation weights. Additionally, we theoretically analyze the convergence properties of GATTA for non-convex loss functions. Numerical results validate the excellent performances of the proposed algorithms in terms of convergence and communication cost.

Distributed ADMM with Synergetic Communication and Computation

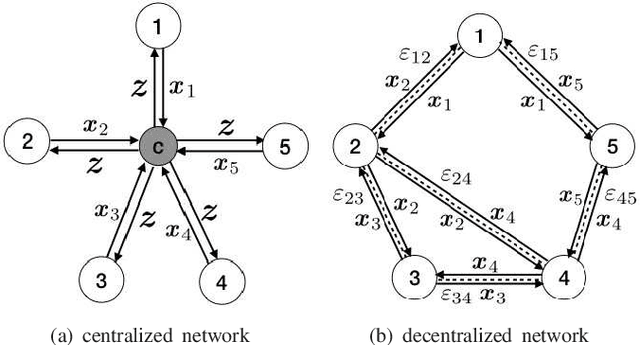
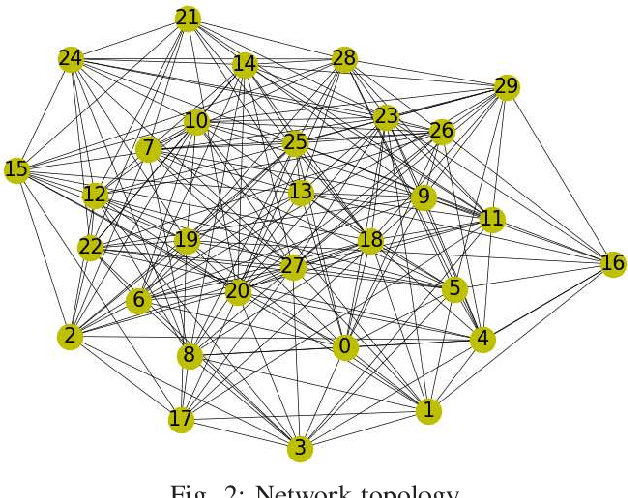
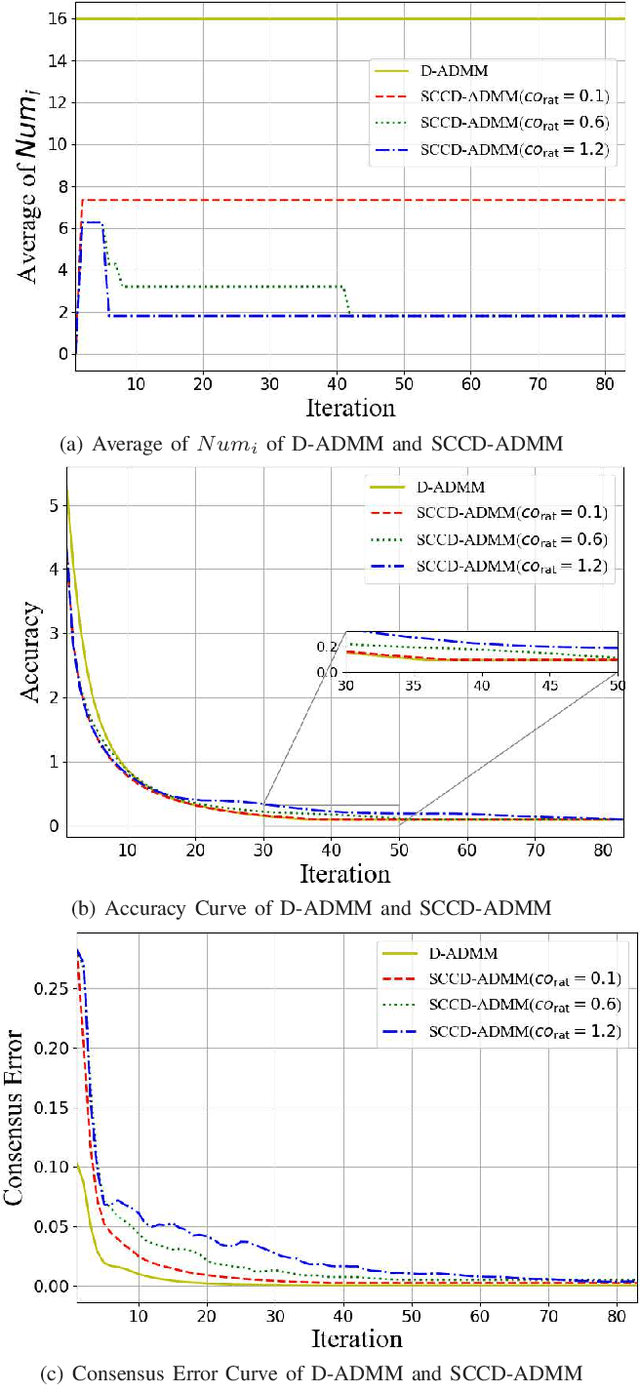
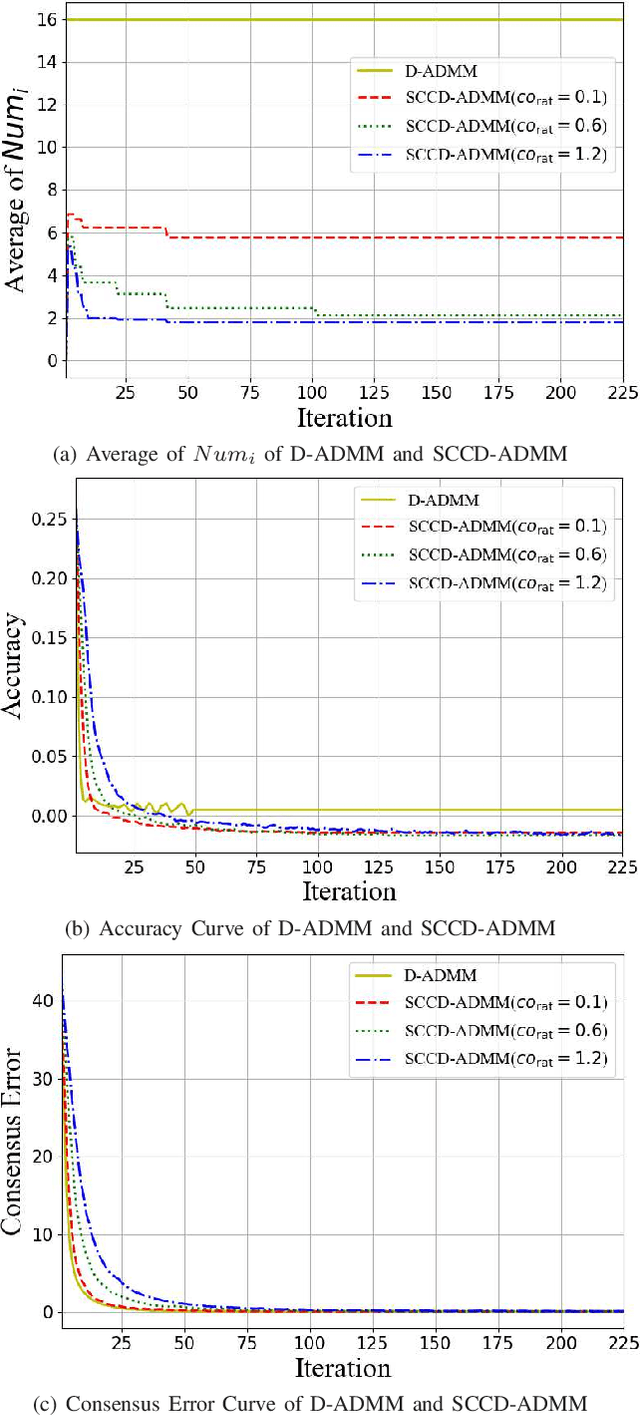
In this paper, we propose a novel distributed alternating direction method of multipliers (ADMM) algorithm with synergetic communication and computation, called SCCD-ADMM, to reduce the total communication and computation cost of the system. Explicitly, in the proposed algorithm, each node interacts with only part of its neighboring nodes, the number of which is progressively determined according to a heuristic searching procedure, which takes into account both the predicted convergence rate and the communication and computation costs at each iteration, resulting in a trade-off between communication and computation. Then the node chooses its neighboring nodes according to an importance sampling distribution derived theoretically to minimize the variance with the latest information it locally stores. Finally, the node updates its local information with a new update rule which adapts to the number of communication nodes. We prove the convergence of the proposed algorithm and provide an upper bound of the convergence variance brought by randomness. Extensive simulations validate the excellent performances of the proposed algorithm in terms of convergence rate and variance, the overall communication and computation cost, the impact of network topology as well as the time for evaluation, in comparison with the traditional counterparts.