Distributed ADMM with Synergetic Communication and Computation
Paper and Code
Sep 29, 2020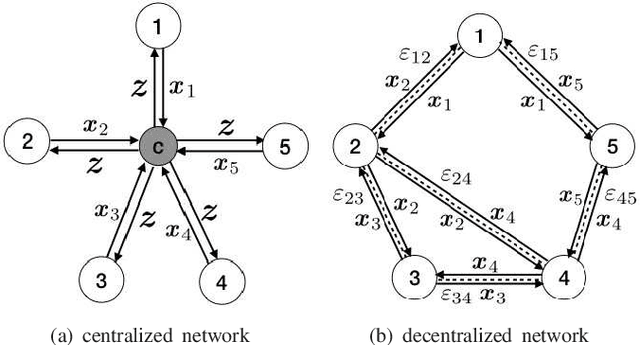
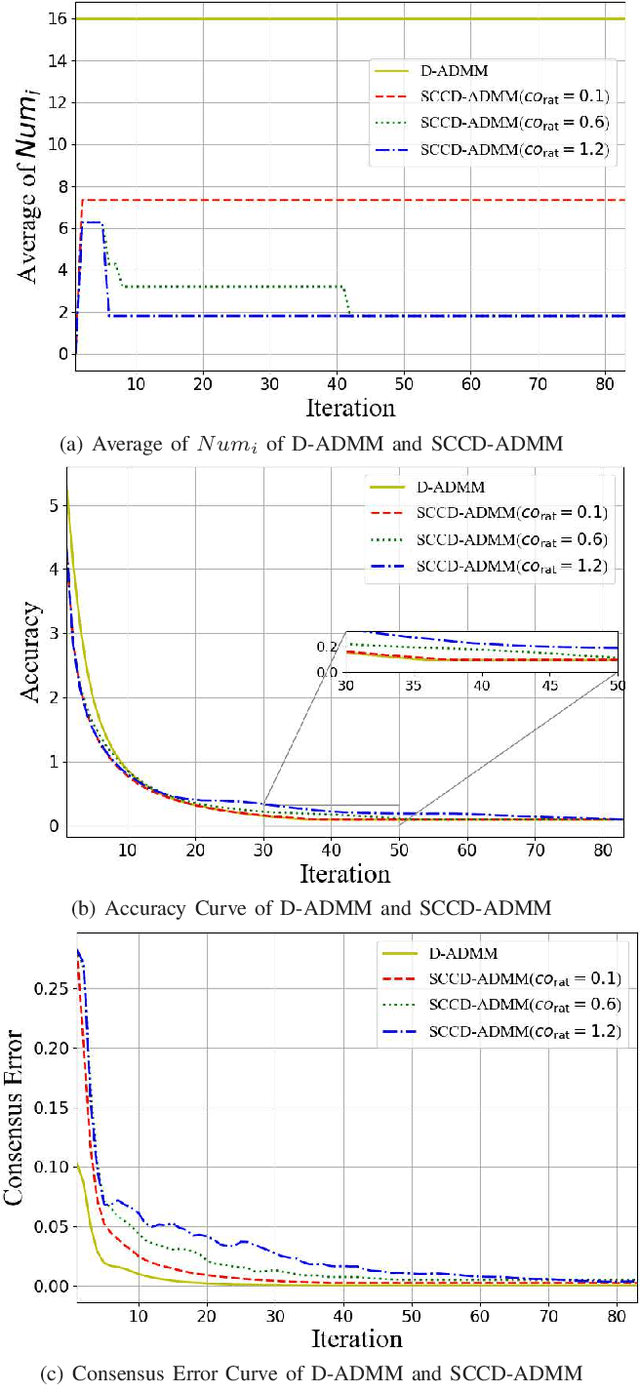
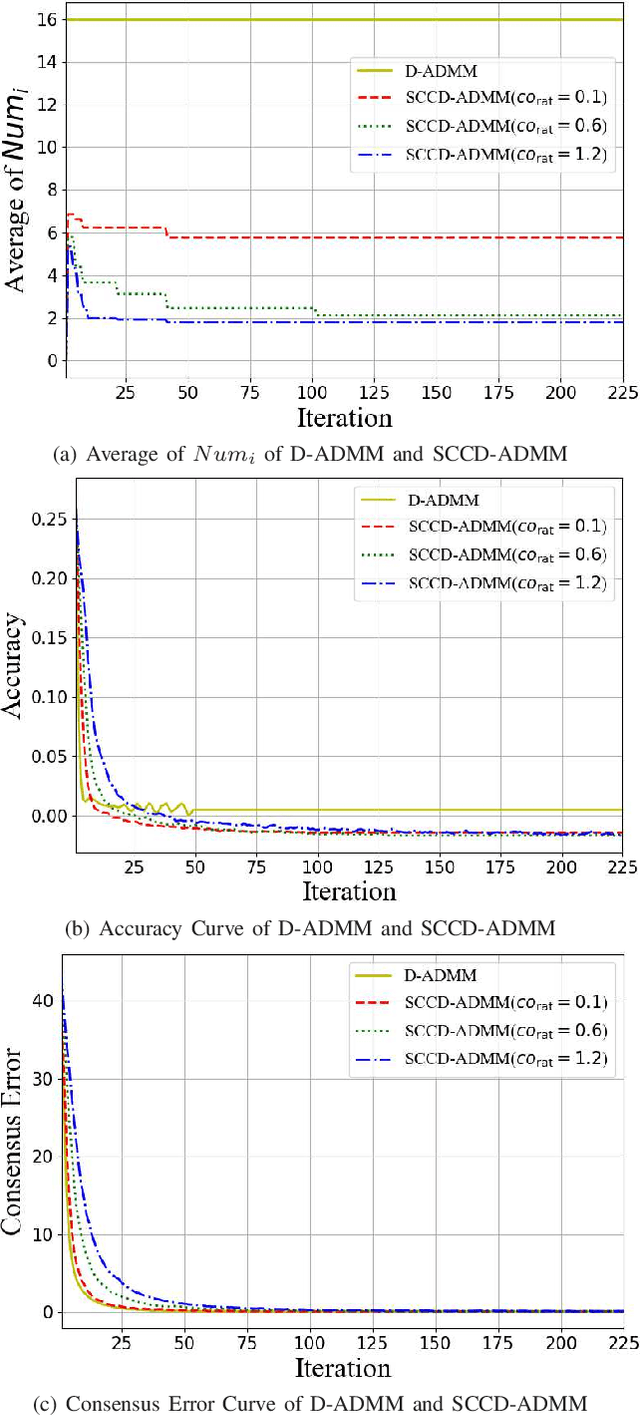
In this paper, we propose a novel distributed alternating direction method of multipliers (ADMM) algorithm with synergetic communication and computation, called SCCD-ADMM, to reduce the total communication and computation cost of the system. Explicitly, in the proposed algorithm, each node interacts with only part of its neighboring nodes, the number of which is progressively determined according to a heuristic searching procedure, which takes into account both the predicted convergence rate and the communication and computation costs at each iteration, resulting in a trade-off between communication and computation. Then the node chooses its neighboring nodes according to an importance sampling distribution derived theoretically to minimize the variance with the latest information it locally stores. Finally, the node updates its local information with a new update rule which adapts to the number of communication nodes. We prove the convergence of the proposed algorithm and provide an upper bound of the convergence variance brought by randomness. Extensive simulations validate the excellent performances of the proposed algorithm in terms of convergence rate and variance, the overall communication and computation cost, the impact of network topology as well as the time for evaluation, in comparison with the traditional counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge