S^2MVTC: a Simple yet Efficient Scalable Multi-View Tensor Clustering

Anchor-based large-scale multi-view clustering has attracted considerable attention for its effectiveness in handling massive datasets. However, current methods mainly seek the consensus embedding feature for clustering by exploring global correlations between anchor graphs or projection matrices.In this paper, we propose a simple yet efficient scalable multi-view tensor clustering (S^2MVTC) approach, where our focus is on learning correlations of embedding features within and across views. Specifically, we first construct the embedding feature tensor by stacking the embedding features of different views into a tensor and rotating it. Additionally, we build a novel tensor low-frequency approximation (TLFA) operator, which incorporates graph similarity into embedding feature learning, efficiently achieving smooth representation of embedding features within different views. Furthermore, consensus constraints are applied to embedding features to ensure inter-view semantic consistency. Experimental results on six large-scale multi-view datasets demonstrate that S^2MVTC significantly outperforms state-of-the-art algorithms in terms of clustering performance and CPU execution time, especially when handling massive data. The code of S^2MVTC is publicly available at https://github.com/longzhen520/S2MVTC.

Deep unfolding Network for Hyperspectral Image Super-Resolution with Automatic Exposure Correction

In recent years, the fusion of high spatial resolution multispectral image (HR-MSI) and low spatial resolution hyperspectral image (LR-HSI) has been recognized as an effective method for HSI super-resolution (HSI-SR). However, both HSI and MSI may be acquired under extreme conditions such as night or poorly illuminating scenarios, which may cause different exposure levels, thereby seriously downgrading the yielded HSISR. In contrast to most existing methods based on respective low-light enhancements (LLIE) of MSI and HSI followed by their fusion, a deep Unfolding HSI Super-Resolution with Automatic Exposure Correction (UHSR-AEC) is proposed, that can effectively generate a high-quality fused HSI-SR (in texture and features) even under very imbalanced exposures, thanks to the correlation between LLIE and HSI-SR taken into account. Extensive experiments are provided to demonstrate the state-of-the-art overall performance of the proposed UHSR-AEC, including comparison with some benchmark peer methods.

Tensor Regression

Regression analysis is a key area of interest in the field of data analysis and machine learning which is devoted to exploring the dependencies between variables, often using vectors. The emergence of high dimensional data in technologies such as neuroimaging, computer vision, climatology and social networks, has brought challenges to traditional data representation methods. Tensors, as high dimensional extensions of vectors, are considered as natural representations of high dimensional data. In this book, the authors provide a systematic study and analysis of tensor-based regression models and their applications in recent years. It groups and illustrates the existing tensor-based regression methods and covers the basics, core ideas, and theoretical characteristics of most tensor-based regression methods. In addition, readers can learn how to use existing tensor-based regression methods to solve specific regression tasks with multiway data, what datasets can be selected, and what software packages are available to start related work as soon as possible. Tensor Regression is the first thorough overview of the fundamentals, motivations, popular algorithms, strategies for efficient implementation, related applications, available datasets, and software resources for tensor-based regression analysis. It is essential reading for all students, researchers and practitioners of working on high dimensional data.

Multi-view MERA Subspace Clustering

Tensor-based multi-view subspace clustering (MSC) can capture high-order correlation in the self-representation tensor. Current tensor decompositions for MSC suffer from highly unbalanced unfolding matrices or rotation sensitivity, failing to fully explore inter/intra-view information. Using the advanced tensor network, namely, multi-scale entanglement renormalization ansatz (MERA), we propose a low-rank MERA based MSC (MERA-MSC) algorithm, where MERA factorizes a tensor into contractions of one top core factor and the rest orthogonal/semi-orthogonal factors. Benefiting from multiple interactions among orthogonal/semi-orthogonal (low-rank) factors, the low-rank MERA has a strong representation power to capture the complex inter/intra-view information in the self-representation tensor. The alternating direction method of multipliers is adopted to solve the optimization model. Experimental results on five multi-view datasets demonstrate MERA-MSC has superiority against the compared algorithms on six evaluation metrics. Furthermore, we extend MERA-MSC by incorporating anchor learning to develop a scalable low-rank MERA based multi-view clustering method (sMREA-MVC). The effectiveness and efficiency of sMERA-MVC have been validated on three large-scale multi-view datasets. To our knowledge, this is the first work to introduce MERA to the multi-view clustering topic. The codes of MERA-MSC and sMERA-MVC are publicly available at https://github.com/longzhen520/MERA-MSC.

Adaptively Topological Tensor Network for Multi-view Subspace Clustering

Multi-view subspace clustering methods have employed learned self-representation tensors from different tensor decompositions to exploit low rank information. However, the data structures embedded with self-representation tensors may vary in different multi-view datasets. Therefore, a pre-defined tensor decomposition may not fully exploit low rank information for a certain dataset, resulting in sub-optimal multi-view clustering performance. To alleviate the aforementioned limitations, we propose the adaptively topological tensor network (ATTN) by determining the edge ranks from the structural information of the self-representation tensor, and it can give a better tensor representation with the data-driven strategy. Specifically, in multi-view tensor clustering, we analyze the higher-order correlations among different modes of a self-representation tensor, and prune the links of the weakly correlated ones from a fully connected tensor network. Therefore, the newly obtained tensor networks can efficiently explore the essential clustering information with self-representation with different tensor structures for various datasets. A greedy adaptive rank-increasing strategy is further applied to improve the capture capacity of low rank structure. We apply ATTN on multi-view subspace clustering and utilize the alternating direction method of multipliers to solve it. Experimental results show that multi-view subspace clustering based on ATTN outperforms the counterparts on six multi-view datasets.

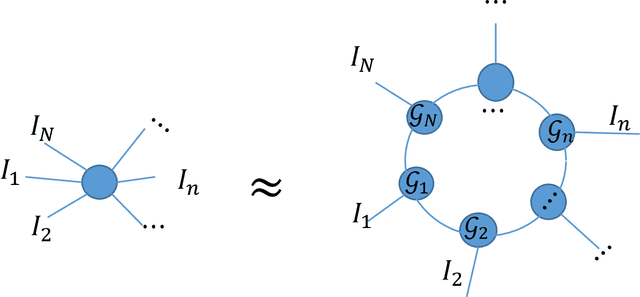
Tucker-O-Minus Decomposition for Multi-view Tensor Subspace Clustering

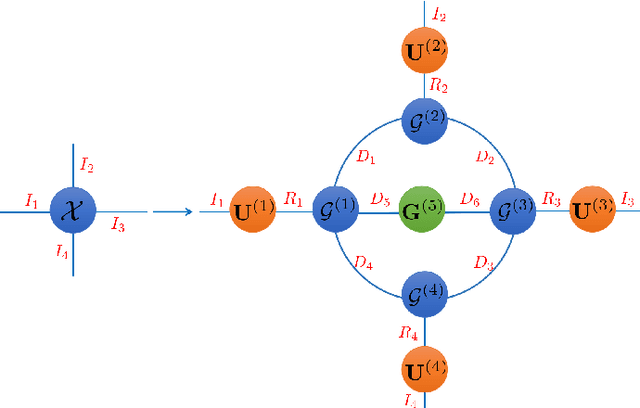
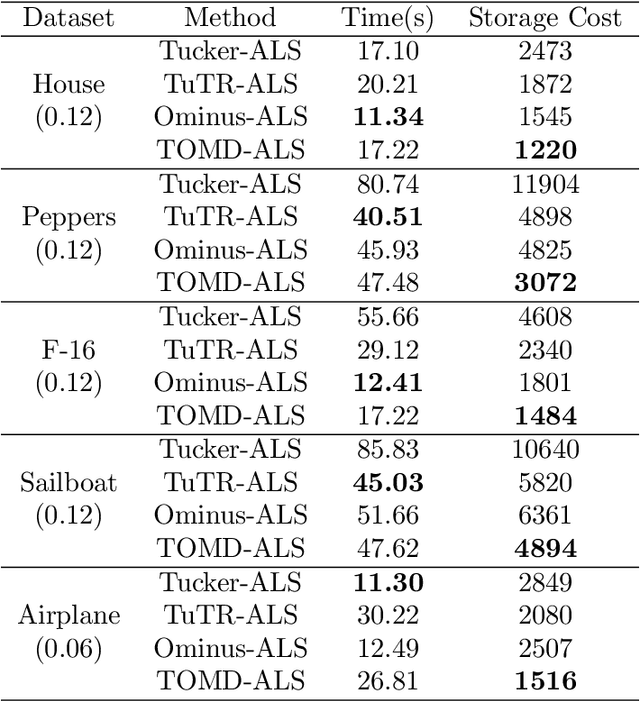
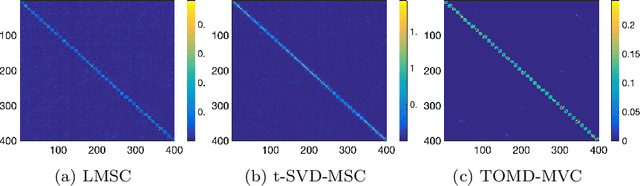
With powerful ability to exploit latent structure of self-representation information, different tensor decompositions have been employed into low rank multi-view clustering (LRMVC) models for achieving significant performance. However, current approaches suffer from a series of problems related to those tensor decomposition, such as the unbalanced matricization scheme, rotation sensitivity, deficient correlations capture and so forth. All these will lead to LRMVC having insufficient access to global information, which is contrary to the target of multi-view clustering. To alleviate these problems, we propose a new tensor decomposition called Tucker-O-Minus Decomposition (TOMD) for multi-view clustering. Specifically, based on the Tucker format, we additionally employ the O-minus structure, which consists of a circle with an efficient bridge linking two weekly correlated factors. In this way, the core tensor in Tucker format is replaced by the O-minus architecture with a more balanced structure, and the enhanced capacity of capturing the global low rank information will be achieved. The proposed TOMD also provides more compact and powerful representation abilities for the self-representation tensor, simultaneously. The alternating direction method of multipliers is used to solve the proposed model TOMD-MVC. Numerical experiments on six benchmark data sets demonstrate the superiority of our proposed method in terms of F-score, precision, recall, normalized mutual information, adjusted rand index, and accuracy.

URIR: Recommendation algorithm of user RNN encoder and item encoder based on knowledge graph

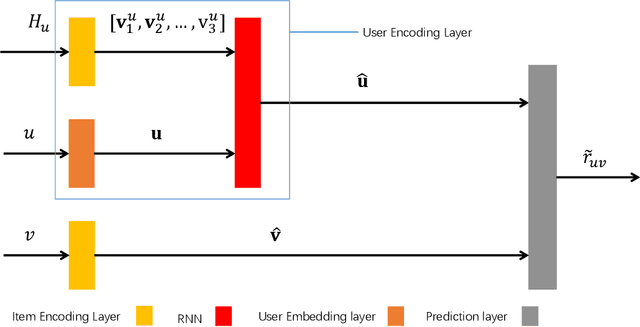
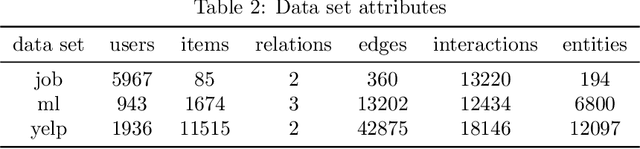
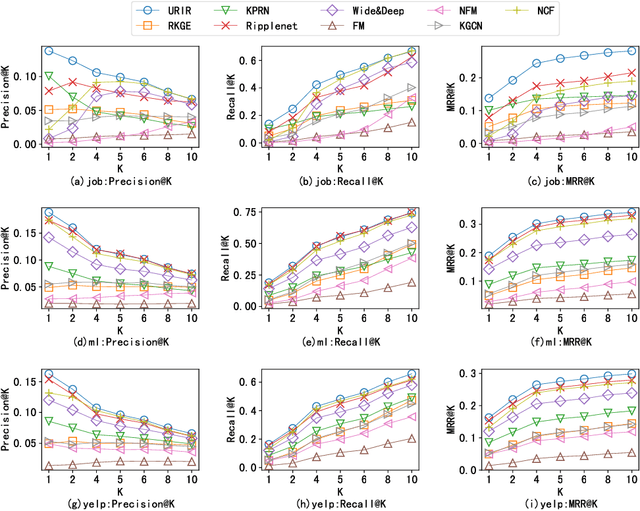
Due to a large amount of information, it is difficult for users to find what they are interested in among the many choices. In order to improve users' experience, recommendation systems have been widely used in music recommendations, movie recommendations, online shopping, and other scenarios. Recently, Knowledge Graph (KG) has been proven to be an effective tool to improve the performance of recommendation systems. However, a huge challenge in applying knowledge graphs for recommendation is how to use knowledge graphs to obtain better user codes and item codes. In response to this problem, this research proposes a user Recurrent Neural Network (RNN) encoder and item encoder recommendation algorithm based on Knowledge Graph (URIR). This study encodes items by capturing high-level neighbor information to generate items' representation vectors and applies an RNN and items' representation vectors to encode users to generate users' representation vectors, and then perform inner product operation on users' representation vectors and items' representation vectors to get probabilities of users interaction with items. Numerical experiments on three real-world datasets demonstrate that URIR is superior performance to state-of-the-art algorithms in indicators such as AUC, Precision, Recall, and MRR. This implies that URIR can effectively use knowledge graph to obtain better user codes and item codes, thereby obtaining better recommendation results.

Bayesian Low Rank Tensor Ring Model for Image Completion

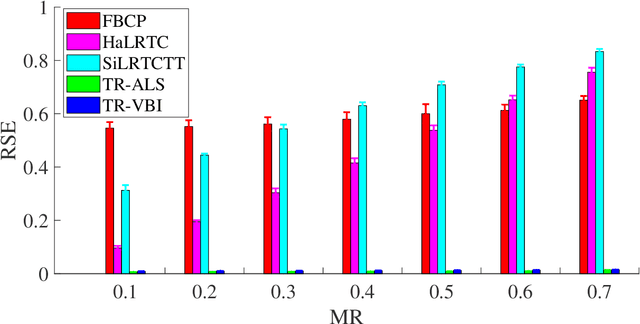
Low rank tensor ring model is powerful for image completion which recovers missing entries in data acquisition and transformation. The recently proposed tensor ring (TR) based completion algorithms generally solve the low rank optimization problem by alternating least squares method with predefined ranks, which may easily lead to overfitting when the unknown ranks are set too large and only a few measurements are available. In this paper, we present a Bayesian low rank tensor ring model for image completion by automatically learning the low rank structure of data. A multiplicative interaction model is developed for the low-rank tensor ring decomposition, where core factors are enforced to be sparse by assuming their entries obey Student-T distribution. Compared with most of the existing methods, the proposed one is free of parameter-tuning, and the TR ranks can be obtained by Bayesian inference. Numerical Experiments, including synthetic data, color images with different sizes and YaleFace dataset B with respect to one pose, show that the proposed approach outperforms state-of-the-art ones, especially in terms of recovery accuracy.

Hyperspectral Image Denoising with Partially Orthogonal Matrix Vector Tensor Factorization

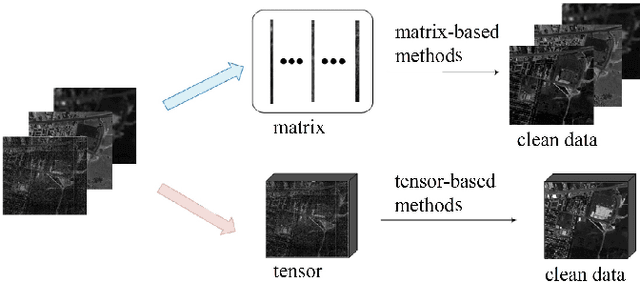
Hyperspectral image (HSI) has some advantages over natural image for various applications due to the extra spectral information. During the acquisition, it is often contaminated by severe noises including Gaussian noise, impulse noise, deadlines, and stripes. The image quality degeneration would badly effect some applications. In this paper, we present a HSI restoration method named smooth and robust low rank tensor recovery. Specifically, we propose a structural tensor decomposition in accordance with the linear spectral mixture model of HSI. It decomposes a tensor into sums of outer matrix vector products, where the vectors are orthogonal due to the independence of endmember spectrums. Based on it, the global low rank tensor structure can be well exposited for HSI denoising. In addition, the 3D anisotropic total variation is used for spatial spectral piecewise smoothness of HSI. Meanwhile, the sparse noise including impulse noise, deadlines and stripes, is detected by the l1 norm regularization. The Frobenius norm is used for the heavy Gaussian noise in some real world scenarios. The alternating direction method of multipliers is adopted to solve the proposed optimization model, which simultaneously exploits the global low rank property and the spatial spectral smoothness of the HSI. Numerical experiments on both simulated and real data illustrate the superiority of the proposed method in comparison with the existing ones.