Yingcong Lu
Adaptively Topological Tensor Network for Multi-view Subspace Clustering
May 01, 2023Abstract:Multi-view subspace clustering methods have employed learned self-representation tensors from different tensor decompositions to exploit low rank information. However, the data structures embedded with self-representation tensors may vary in different multi-view datasets. Therefore, a pre-defined tensor decomposition may not fully exploit low rank information for a certain dataset, resulting in sub-optimal multi-view clustering performance. To alleviate the aforementioned limitations, we propose the adaptively topological tensor network (ATTN) by determining the edge ranks from the structural information of the self-representation tensor, and it can give a better tensor representation with the data-driven strategy. Specifically, in multi-view tensor clustering, we analyze the higher-order correlations among different modes of a self-representation tensor, and prune the links of the weakly correlated ones from a fully connected tensor network. Therefore, the newly obtained tensor networks can efficiently explore the essential clustering information with self-representation with different tensor structures for various datasets. A greedy adaptive rank-increasing strategy is further applied to improve the capture capacity of low rank structure. We apply ATTN on multi-view subspace clustering and utilize the alternating direction method of multipliers to solve it. Experimental results show that multi-view subspace clustering based on ATTN outperforms the counterparts on six multi-view datasets.
Tucker-O-Minus Decomposition for Multi-view Tensor Subspace Clustering
Oct 23, 2022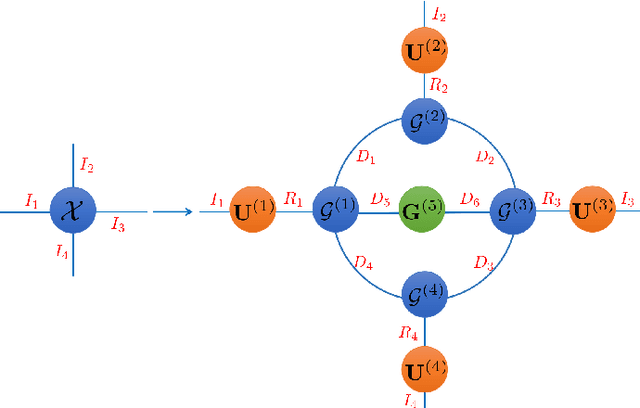

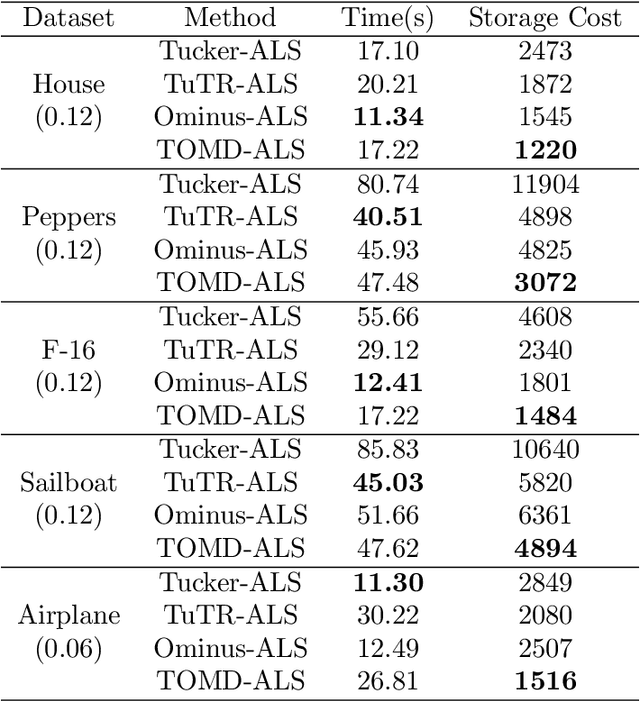
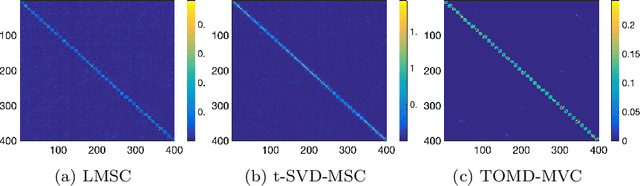
Abstract:With powerful ability to exploit latent structure of self-representation information, different tensor decompositions have been employed into low rank multi-view clustering (LRMVC) models for achieving significant performance. However, current approaches suffer from a series of problems related to those tensor decomposition, such as the unbalanced matricization scheme, rotation sensitivity, deficient correlations capture and so forth. All these will lead to LRMVC having insufficient access to global information, which is contrary to the target of multi-view clustering. To alleviate these problems, we propose a new tensor decomposition called Tucker-O-Minus Decomposition (TOMD) for multi-view clustering. Specifically, based on the Tucker format, we additionally employ the O-minus structure, which consists of a circle with an efficient bridge linking two weekly correlated factors. In this way, the core tensor in Tucker format is replaced by the O-minus architecture with a more balanced structure, and the enhanced capacity of capturing the global low rank information will be achieved. The proposed TOMD also provides more compact and powerful representation abilities for the self-representation tensor, simultaneously. The alternating direction method of multipliers is used to solve the proposed model TOMD-MVC. Numerical experiments on six benchmark data sets demonstrate the superiority of our proposed method in terms of F-score, precision, recall, normalized mutual information, adjusted rand index, and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge