Gemma 2: Improving Open Language Models at a Practical Size

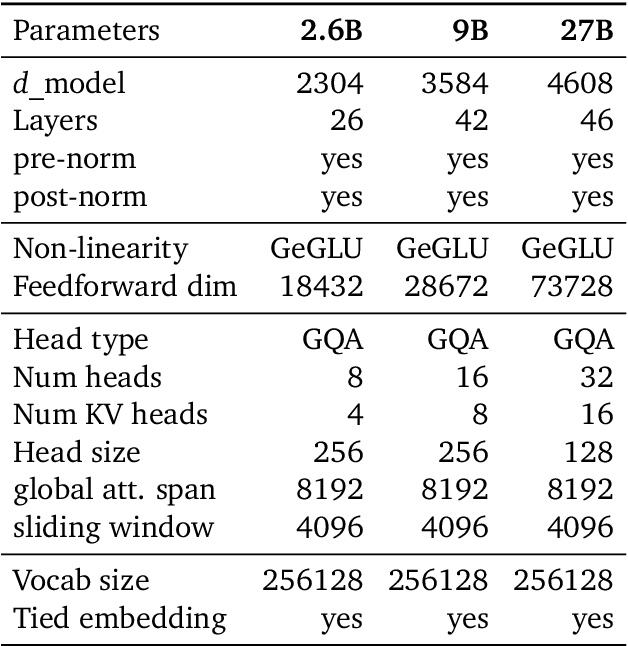
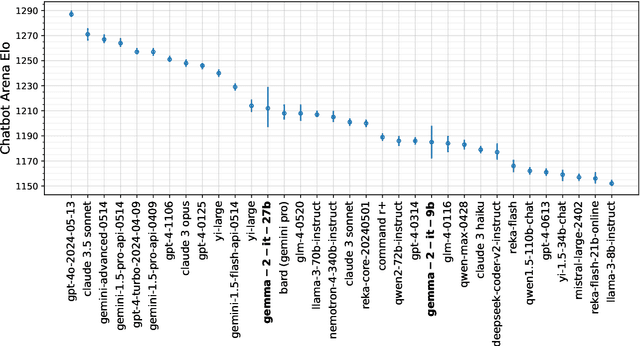
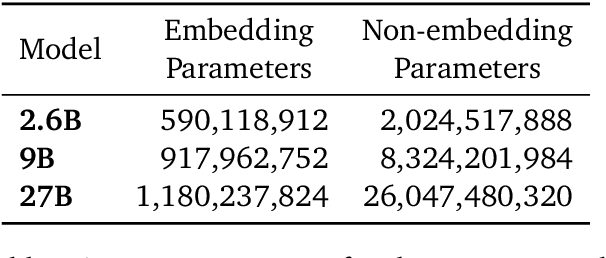
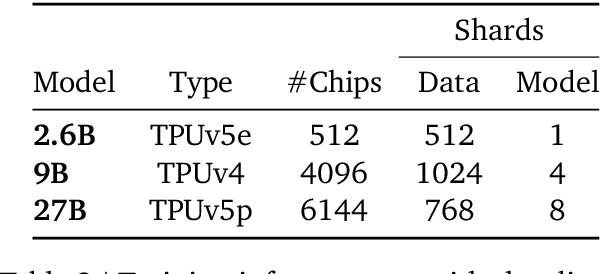
In this work, we introduce Gemma 2, a new addition to the Gemma family of lightweight, state-of-the-art open models, ranging in scale from 2 billion to 27 billion parameters. In this new version, we apply several known technical modifications to the Transformer architecture, such as interleaving local-global attentions (Beltagy et al., 2020a) and group-query attention (Ainslie et al., 2023). We also train the 2B and 9B models with knowledge distillation (Hinton et al., 2015) instead of next token prediction. The resulting models deliver the best performance for their size, and even offer competitive alternatives to models that are 2-3 times bigger. We release all our models to the community.

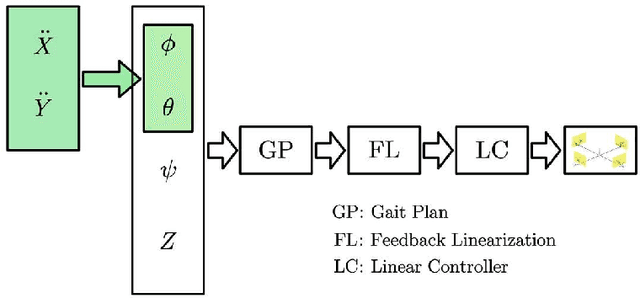
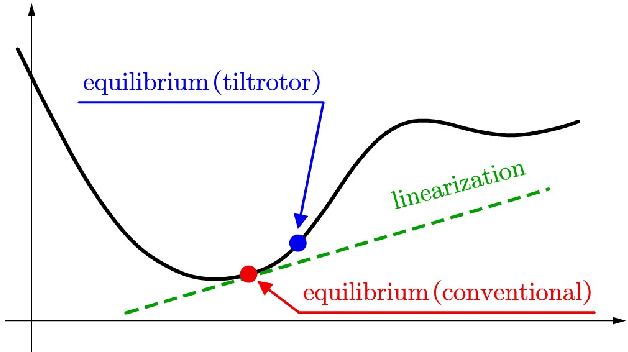
Advanced Feedback Linearization Control for Tiltrotor UAVs: Gait Plan, Controller Design, and Stability Analysis

Three challenges, however, can hinder the application of Feedback Linearization: over-intensive control signals, singular decoupling matrix, and saturation. Activating any of these three issues can challenge the stability proof. To solve these three challenges, first, this research proposed the drone gait plan. The gait plan was initially used to figure out the control problems in quadruped (four-legged) robots; applying this approach, accompanied by Feedback Linearization, the quality of the control signals was enhanced. Then, we proposed the concept of unacceptable attitude curves, which are not allowed for the tiltrotor to travel to. The Two Color Map Theorem was subsequently established to enlarge the supported attitude for the tiltrotor. These theories were employed in the tiltrotor tracking problem with different references. Notable improvements in the control signals were witnessed in the tiltrotor simulator. Finally, we explored the control theory, the stability proof of the novel mobile robot (tilt vehicle) stabilized by Feedback Linearization with saturation. Instead of adopting the tiltrotor model, which is over-complicated, we designed a conceptual mobile robot (tilt-car) to analyze the stability proof. The stability proof (stable in the sense of Lyapunov) was found for a mobile robot (tilt vehicle) controlled by Feedback Linearization with saturation for the first time. The success tracking result with the promising control signals in the tiltrotor simulator demonstrates the advances of our control method. Also, the Lyapunov candidate and the tracking result in the mobile robot (tilt-car) simulator confirm our deductions of the stability proof. These results reveal that these three challenges in Feedback Linearization are solved, to some extents.

Generalized Two Color Map Theorem -- Complete Theorem of Robust Gait Plan for a Tilt-rotor

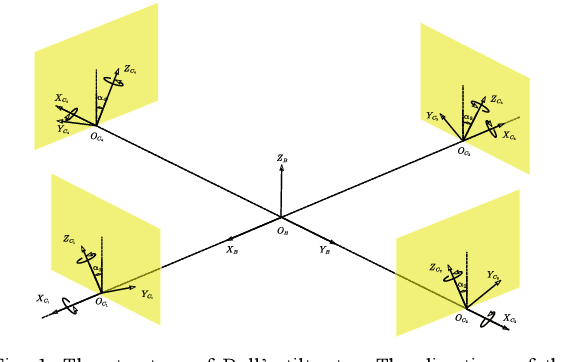
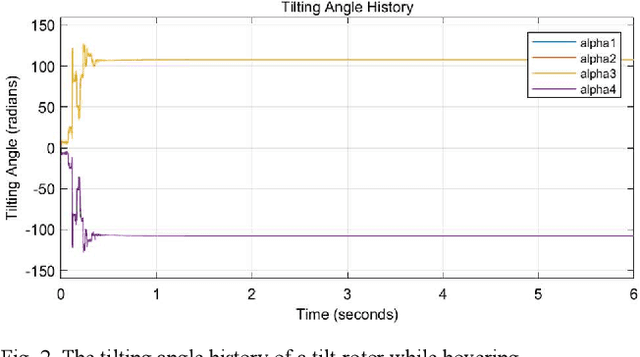
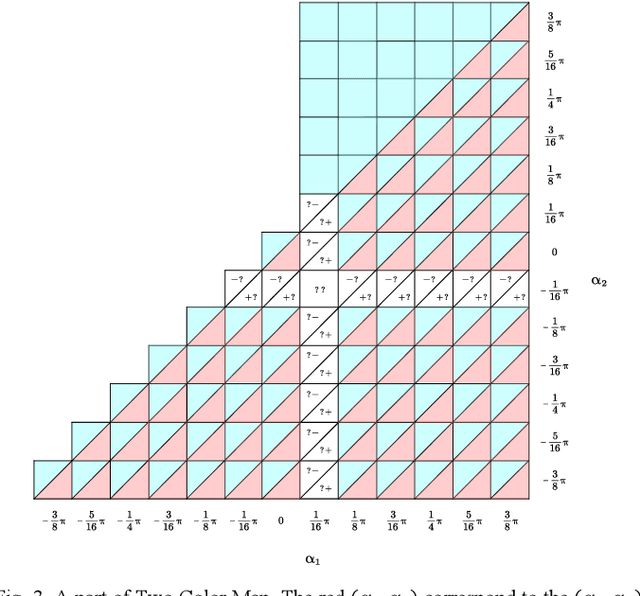
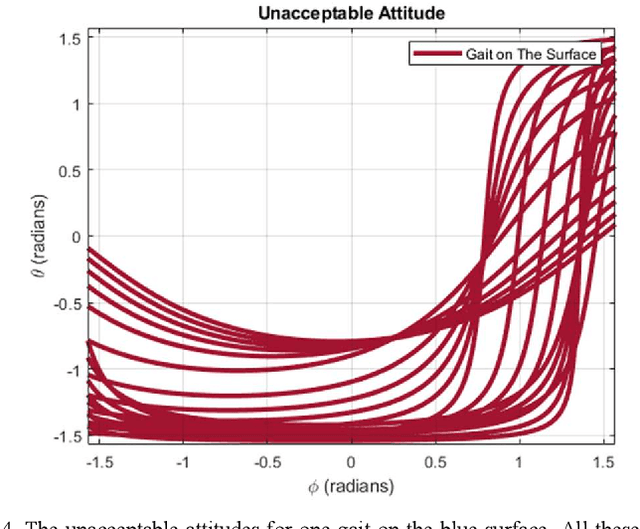
Gait plan is a procedure that is typically applied on the ground robots, e.g., quadrupedal robots; the tilt-rotor, a novel type of quadrotor with eight inputs, is not one of them. While controlling the tilt-rotor relying on feedback linearization, the tilting angles (inputs) are expected to change over-intensively, which may not be expected in the application. To help suppress the intensive change in the tilting angles, a gait plan procedure is introduced to the tilt-rotor before feedback linearization. The tilting angles are specified with time in advance by users rather than given by the control rule. However, based on this scenario, the decoupling matrix in feedback linearization can be singular for some attitudes, combinations of roll angle and pitch angle. It hinders the further application of the feedback linearization. With this concern, Two Color Map Theorem is established to maximize the acceptable attitude region, where the combinations of roll and pitch will give an invertible decoupling matrix. That theorem, however, over-restricts the choice of the tilting angles, which can rule out some feasible robust gaits. This paper gives the generalized Two Color Map Theorem; all the robust gaits can be found based on this generalized theorem. The robustness of three gaits that satisfy this generalized Two Color Map Theorem (while violating Two Color Map Theorem) are analyzed. The results show that Generalized Two Color Map Theorem completes the search for the robust gaits for a tilt-rotor.

The Robust Gait of a Tilt-rotor and Its Application to Tracking Control -- Application of Two Color Map Theorem

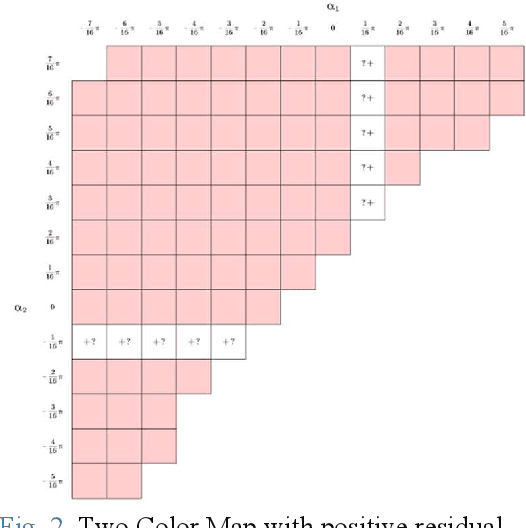
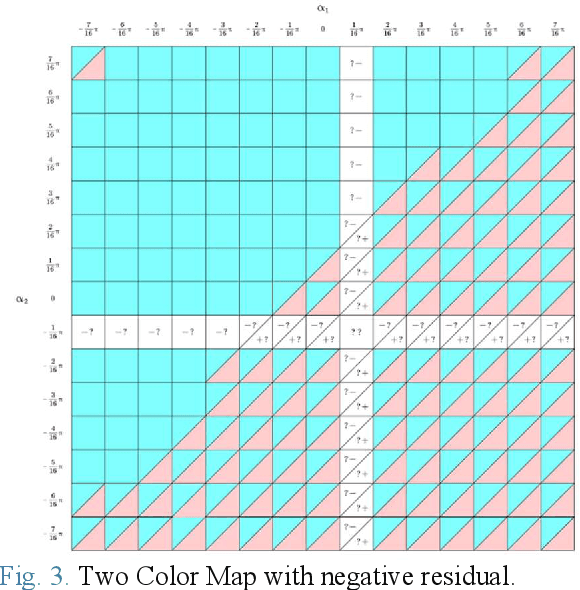
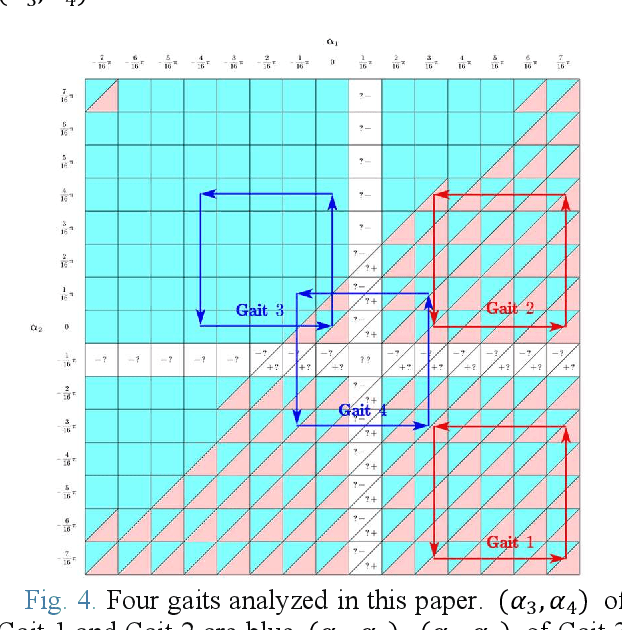
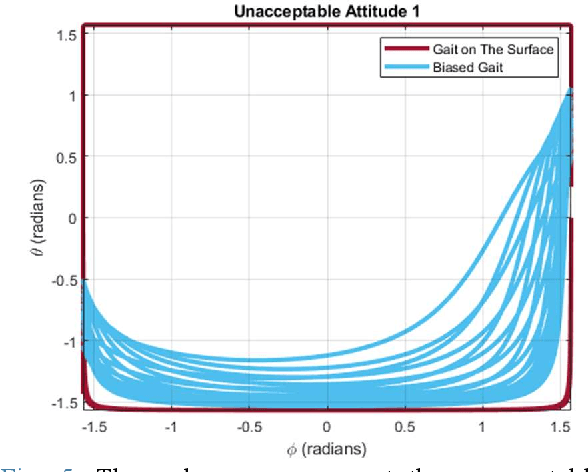
Rylls tilt-rotor is a UAV with eight inputs; the four magnitudes of the thrusts as well as four tilting angles of the thrusts can be specified in need, e.g., based on a control rule. Despite of the success in simulation, conventional feedback linearization witnesses the over-intensive change in the inputs while applying to stabilize Rylls tilt-rotor. Our previous research thus put the extra procedure named gait plan forward to suppress the unexpected changes in the tilting angles. Accompanying the Two Color Map Theorem, the tilting-angles are planned robustly and continuously. The designed gaits are robust to the change of the attitude. However, this is not a complete theory before further applying to the tracking simulation test. This paper further discusses some gaits following the Two Color Map Theorem and simulates a tracking problem for a tilt-rotor. A uniform circular moving reference is designed to be tracked by the tilt-rotor equipped with the designed robust gait and the feedback linearization controller. The gaits satisfying Two Color Map Theorem show the robustness. The results from the simulation show the success in tracking of the tilt-rotor.

Four-dimensional Gait Surfaces for A Tilt-rotor -- Two Color Map Theorem

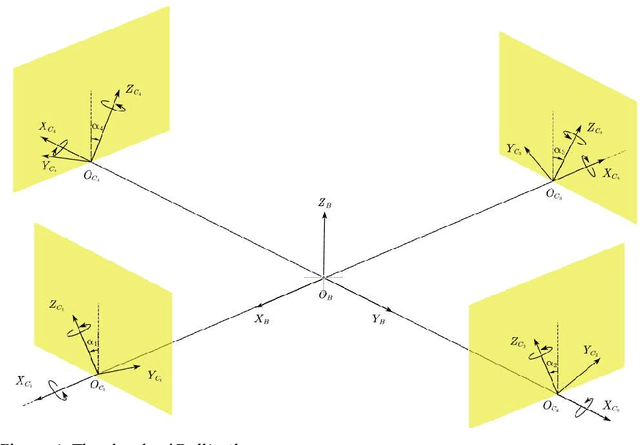
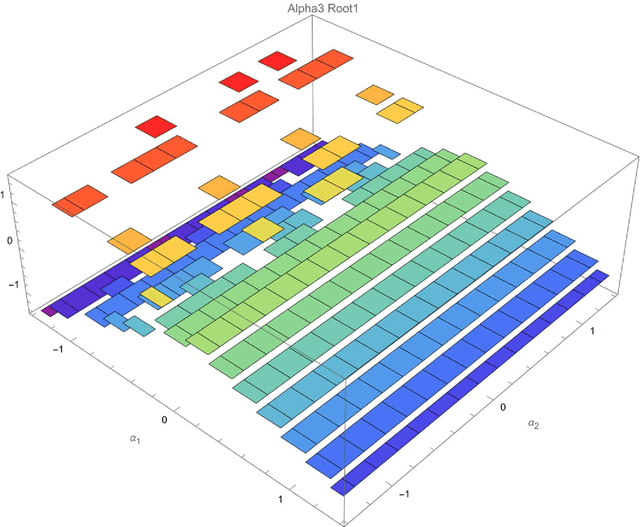
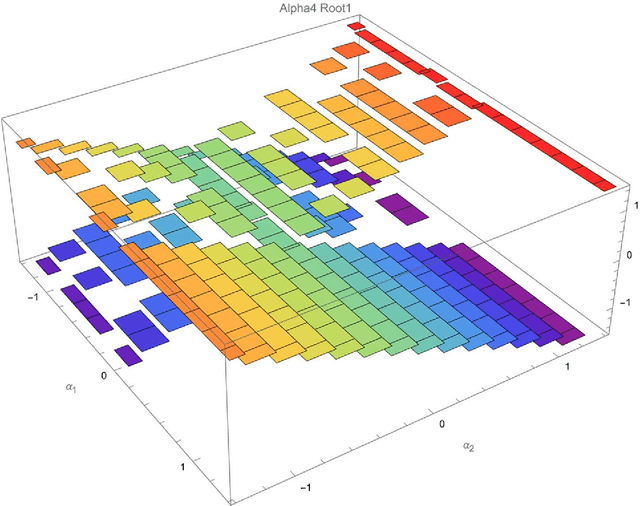
This article presents the four-dimensional surfaces which instruct the gait plan for a tilt-rotor. The previous gaits analyzed in the tilt-rotor research are inspired by animals; no theoretical base backs the robustness of these gaits. This research deduces the gaits by diminishing the effect of the attitude of the tilt-rotor for the first time. Four-dimensional gait surfaces are subsequently found, on which the gaits are expected to be robust to the attitude. These surfaces provide the region where the gait is suggested to be planned. However, a discontinuous region may hinder the gait plan process while utilizing the proposal gait surfaces. A Two Color Map Theorem is then established to guarantee the continuity of each gait designed. The robustness of the typical gaits obeying the Two Color Map Theorem and on the gait surface is demonstrated by comparing the singular curve in attitude with the gaits not on the gait surface. The result shows that the acceptable attitudes enlarge for the gaits on the gait surface.

Cat-inspired Gaits for A Tilt-rotor -- from Symmetrical to Asymmetrical

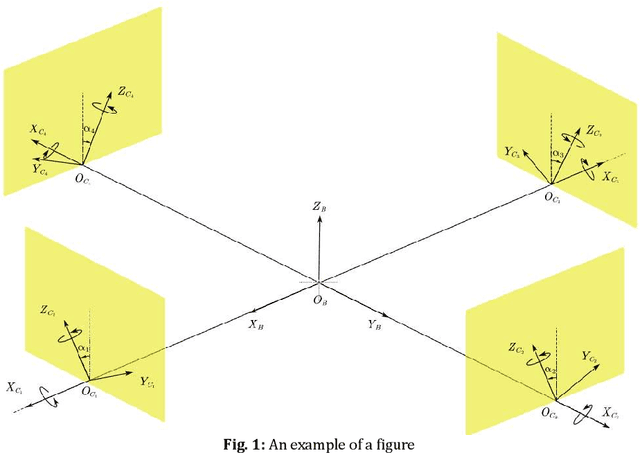
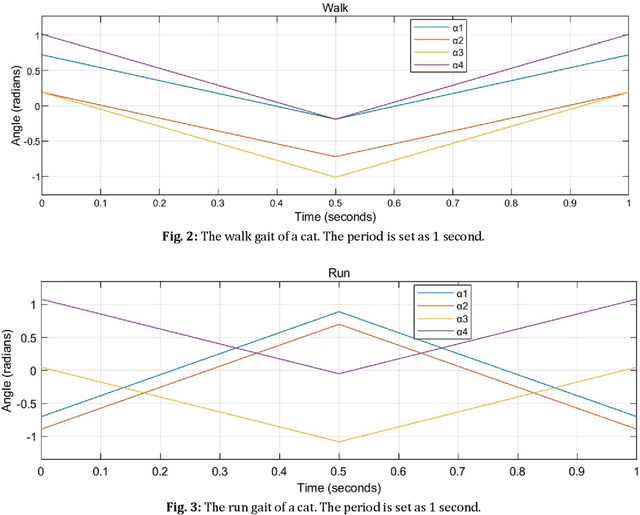
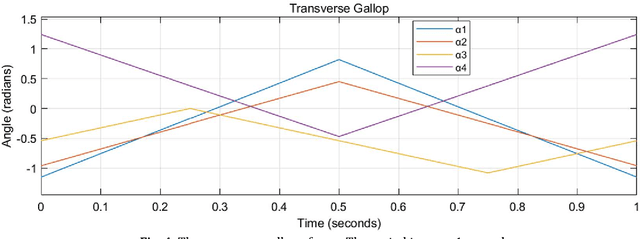
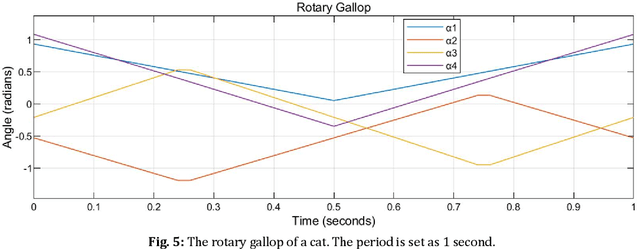
Among the tilt-rotors (quadrotors) developed in the last decades, Rylls model with eight inputs (four magnitudes of the thrusts and four tilting angles) attracted great attention. Typical feedback linearization maneuvers all the eight inputs with a united control rule to stabilize this tilt-rotor. Instead of assigning the tilting angles by the control rule, the recent research predetermined the tilting angles and left the magnitudes of the thrusts the only control signals. These tilting angles are designed to mimic the cat-trot gait, avoiding the singular decoupling matrix feedback linearization. To complete the discussions of the cat-gaits inspired tilt-rotor gaits, this research addresses the analyses on the rest of the common cat gaits, walk, run, transverse gallop, and rotary gallop. It is found that the singular decoupling matrix exist in walk gait and rotary gallop. Further modifications are conducted to these two gaits to accommodate the application of feedback linearization. The modified gaits with different periods are then applied to the tilt-rotor in tracking experiments, in which the references are uniform rectilinear motion and uniform circular motion. All the experiments are simulated in Simulink, MATLAB. The result shows that.

Feedback Linearization Based Tracking Control of A Tilt-rotor with Cat-trot Gait Plan

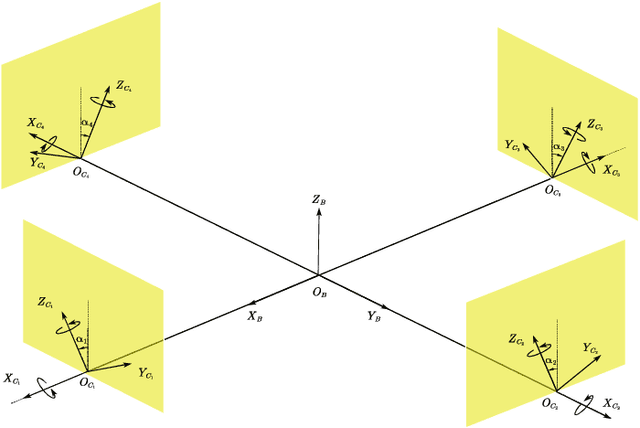
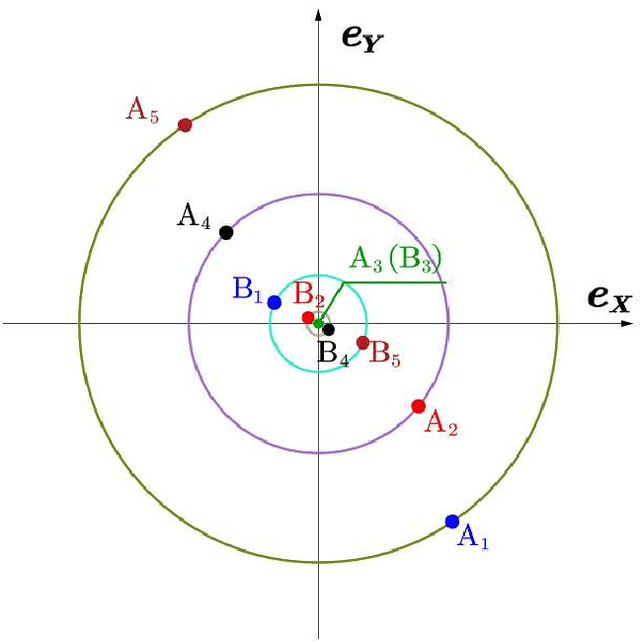
With the introduction of the laterally bounded forces, the tilt-rotor gains more flexibility in the controller design. Typical Feedback Linearization methods of controlling this vehicle utilize all the inputs; the magnitudes as well as the directions of the thrusts are maneuvered simultaneously based on a unified control rule. Although several promising results indicate that these controllers may track the desired complicated trajectories, the tilting angles are required to change relatively fast or in large scale during the flight. This problem challenges the applicability of these control algorithms. The recent idea in sacrifice the number of input and deem the tilt-rotor an under-actuated system may solve this problem; the tilting angles are fixed or vary in a predetermined pattern without being maneuvered by the control algorithm. By careful avoidance of the singular decoupling matrix, several attitudes can be tracked without changing the tilting angles unexpectedly. While the position was not directly regulated by the Feedback Linearization methods in that research, which left the position-tracking still an open question. In this research, we elucidate the coupling relationship between the position and the attitude. Based on this, we design the position-tracking controller adopting Feedback Linearization. We also plan the gait for the tilt-rotor based on the cat-trot gait. The controller is verified in Simulink, MATLAB. Three types of references are designed for our tracking experiments: setpoint, uniform rectilinear motion, and uniform circular motion. The significant improvement with less steady state error is witnessed after equipping with our modified position-attitude decoupler. This steady state error is also influenced by the frequency of the cat-trot gait.

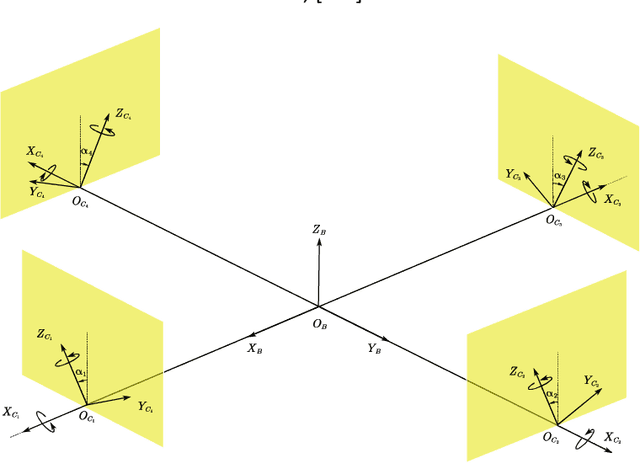
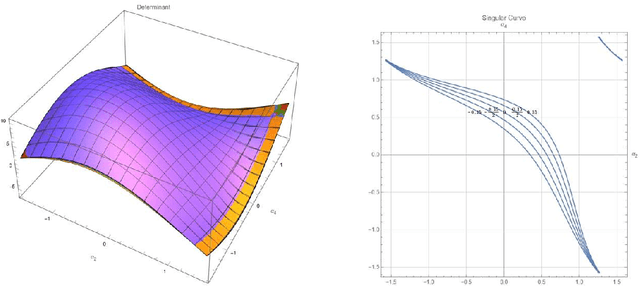
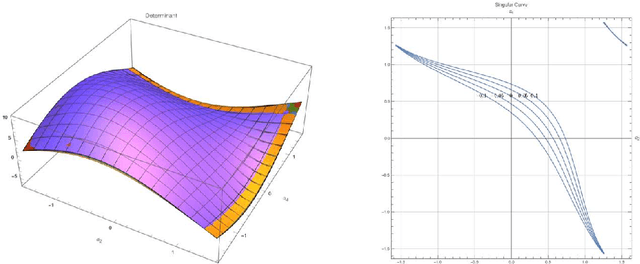
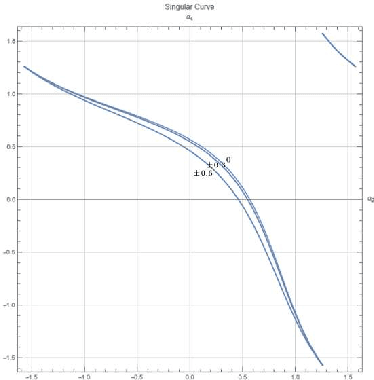
Gait Analysis for A Tilt-rotor: The Dynamic Invertible Gait

Feedback linearization is a popular control method for controlling the tilt-rotor. Despite the fact that this method brings the opportunities to utilize the over-actuated property of the system, typical results indicate the large change in tilting angles, which is not expected in practical. To solve this problem, we introduce the novel concept UAV gait to restrict the tilting angles. Gait plan problem was initially to solve the control problems for quadruped (four-legged) robots. While transplanting this approach, accompanying with the Feedback Linearization method, to the tilt-rotor may cause the well-known non-invertible problem in the decoupling matrix. In this research, we explore the invertible gait for the tilt-rotor and apply the feedback linearization to stabilize the attitude and the altitude. The result is verified in Simulink, MATLAB.

Quad-cone-rotor: A Novel Tilt Quadrotor with Severe-fault-tolerant Ability

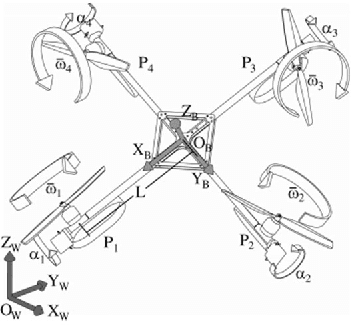
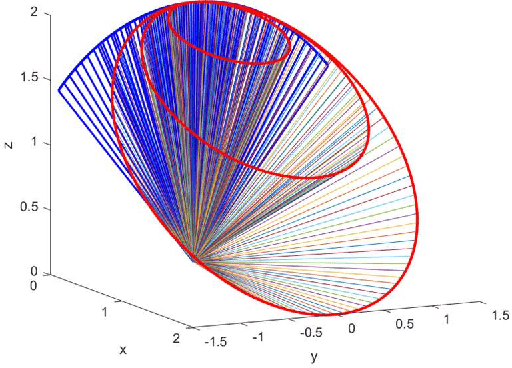
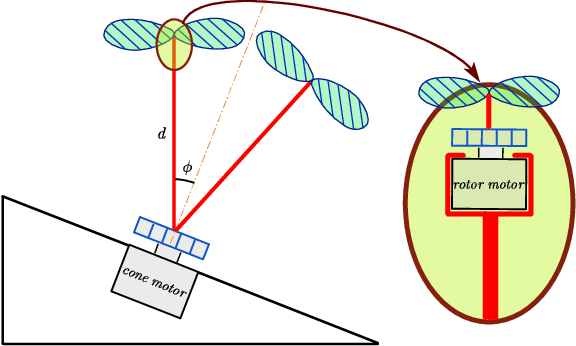
Conventional quadrotors received great attention in trajectory design and fault-tolerant control in these years. The direction of each thrust is perpendicular to the body because of the geometrics in mechanical design. Comparing with the conventional quadrotor, a novel quadrotor named quad-tilt-rotor brings better freedom in manipulating the thrust vector. Quad-tilt-rotor augments the additional degrees of freedom in the thrust, providing the possibility of violating the normal direction of the thrust in the conventional quadrotor. This provides the ability of greater agility in control. This paper presents a novel design of a quad-tilt-rotor (quad-cone-rotor) whose thrust can be assigned along the edge of a cone shape. Besides the inheriting merits in agile from quad-tilt-rotor, the quad-cone-rotor is expected to take fault-tolerant control in severe dynamic failure (total loss in all thrusts). We simulate the control result in a UAV simulator in SIMULINK, MATLAB.

Identification of splicing edges in tampered image based on Dichromatic Reflection Model

Imaging is a sophisticated process combining a plenty of photovoltaic conversions, which lead to some spectral signatures beyond visual perception in the final images. Any manipulation against an original image will destroy these signatures and inevitably leave some traces in the final forgery. Therefore we present a novel optic-physical method to discriminate splicing edges from natural edges in a tampered image. First, we transform the forensic image from RGB into color space of S and o1o2. Then on the assumption of Dichromatic Reflection Model, edges in the image are discovered by composite gradient and classified into different types based on their different photometric properties. Finally, splicing edges are reserved against natural ones by a simple logical algorithm. Experiment results show the efficacy of the proposed method.