Generalized Two Color Map Theorem -- Complete Theorem of Robust Gait Plan for a Tilt-rotor
Paper and Code
Jun 27, 2022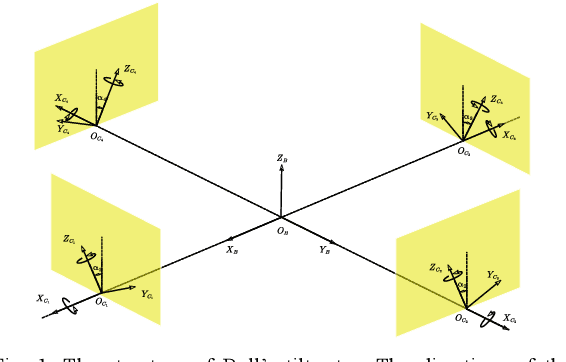
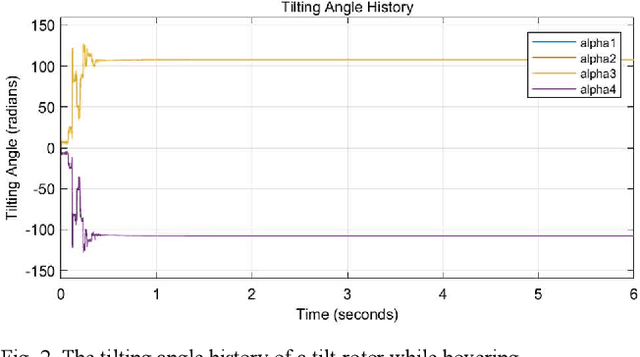
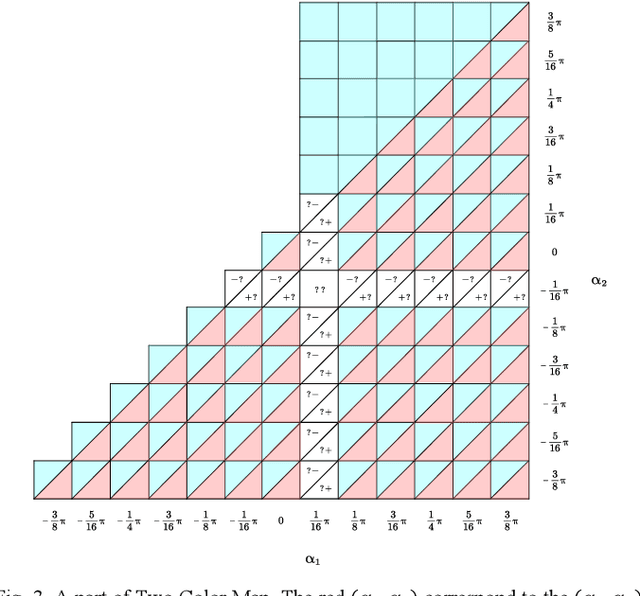
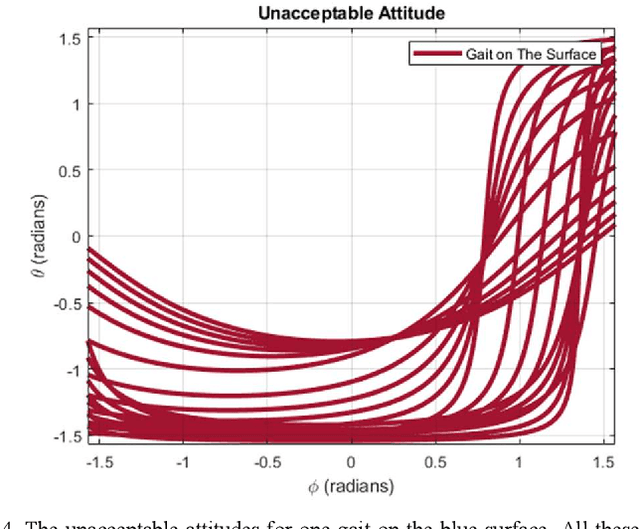
Gait plan is a procedure that is typically applied on the ground robots, e.g., quadrupedal robots; the tilt-rotor, a novel type of quadrotor with eight inputs, is not one of them. While controlling the tilt-rotor relying on feedback linearization, the tilting angles (inputs) are expected to change over-intensively, which may not be expected in the application. To help suppress the intensive change in the tilting angles, a gait plan procedure is introduced to the tilt-rotor before feedback linearization. The tilting angles are specified with time in advance by users rather than given by the control rule. However, based on this scenario, the decoupling matrix in feedback linearization can be singular for some attitudes, combinations of roll angle and pitch angle. It hinders the further application of the feedback linearization. With this concern, Two Color Map Theorem is established to maximize the acceptable attitude region, where the combinations of roll and pitch will give an invertible decoupling matrix. That theorem, however, over-restricts the choice of the tilting angles, which can rule out some feasible robust gaits. This paper gives the generalized Two Color Map Theorem; all the robust gaits can be found based on this generalized theorem. The robustness of three gaits that satisfy this generalized Two Color Map Theorem (while violating Two Color Map Theorem) are analyzed. The results show that Generalized Two Color Map Theorem completes the search for the robust gaits for a tilt-rotor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge