Review of PID Controller Applications for UAVs

Unmanned Aerial Vehicles (UAVs) have gained widespread recognition for their diverse applications, ranging from surveillance to delivery services. Among the various control algorithms employed to stabilize and navigate UAVs, the Proportional-Integral-Derivative (PID) controller stands out as a classical yet robust solution. This review provides a comprehensive examination of PID controller applications in the context of UAVs, addressing their fundamental principles, dynamics modeling, stability control, navigation tasks, parameter tuning methods, challenges, and future directions.

Geometric and Feedback Linearization on UAV: Review

The pervasive integration of Unmanned Aerial Vehicles (UAVs) across multifarious domains necessitates a nuanced understanding of control methodologies to ensure their optimal functionality. This exhaustive review meticulously examines two pivotal control paradigms in the UAV landscape, Geometric Control and Feedback Linearization. Delving into the intricate theoretical underpinnings, practical applications, strengths, and challenges of these methodologies, the paper endeavors to provide a comprehensive overview. Geometric Control, grounded in the principles of differential geometry, offers an elegant and intuitive approach to trajectory tracking and mission execution. In contrast, Feedback Linearization employs nonlinear control techniques to linearize UAV dynamics, paving the way for enhanced controllability. This review not only dissects the theoretical foundations but also scrutinizes real-world applications, integration challenges, and the ongoing research trajectory of Geometric Control and Feedback Linearization in the realm of UAVs.

Generalized Two Color Map Theorem -- Complete Theorem of Robust Gait Plan for a Tilt-rotor

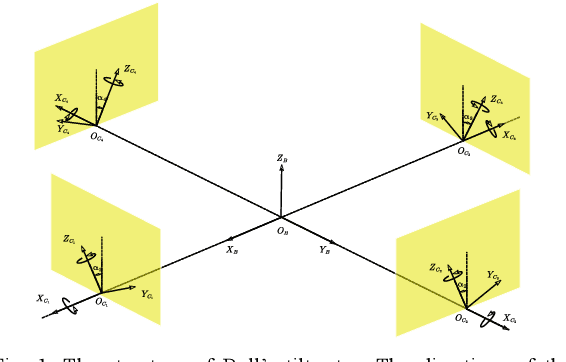
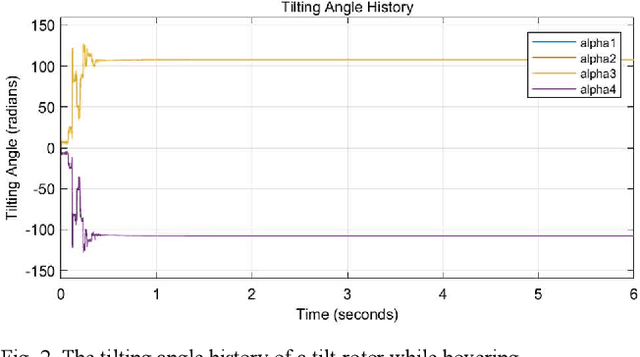
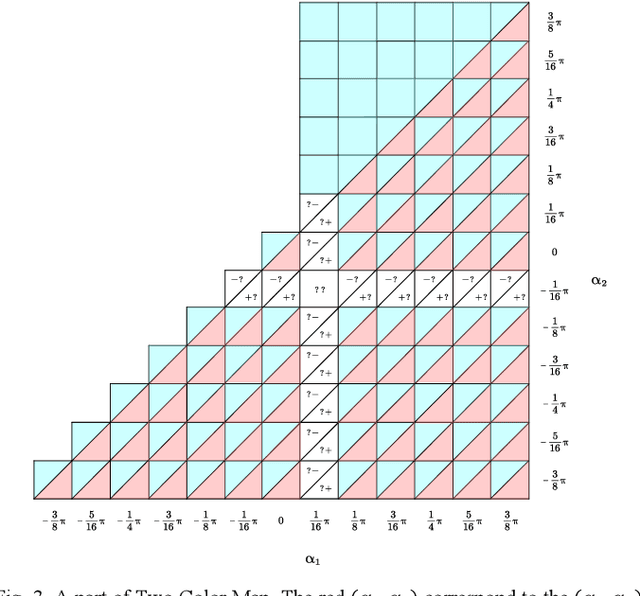
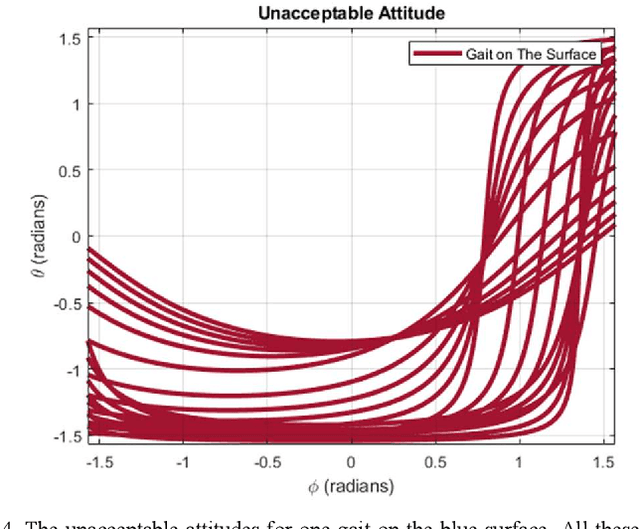
Gait plan is a procedure that is typically applied on the ground robots, e.g., quadrupedal robots; the tilt-rotor, a novel type of quadrotor with eight inputs, is not one of them. While controlling the tilt-rotor relying on feedback linearization, the tilting angles (inputs) are expected to change over-intensively, which may not be expected in the application. To help suppress the intensive change in the tilting angles, a gait plan procedure is introduced to the tilt-rotor before feedback linearization. The tilting angles are specified with time in advance by users rather than given by the control rule. However, based on this scenario, the decoupling matrix in feedback linearization can be singular for some attitudes, combinations of roll angle and pitch angle. It hinders the further application of the feedback linearization. With this concern, Two Color Map Theorem is established to maximize the acceptable attitude region, where the combinations of roll and pitch will give an invertible decoupling matrix. That theorem, however, over-restricts the choice of the tilting angles, which can rule out some feasible robust gaits. This paper gives the generalized Two Color Map Theorem; all the robust gaits can be found based on this generalized theorem. The robustness of three gaits that satisfy this generalized Two Color Map Theorem (while violating Two Color Map Theorem) are analyzed. The results show that Generalized Two Color Map Theorem completes the search for the robust gaits for a tilt-rotor.

Four-dimensional Gait Surfaces for A Tilt-rotor -- Two Color Map Theorem

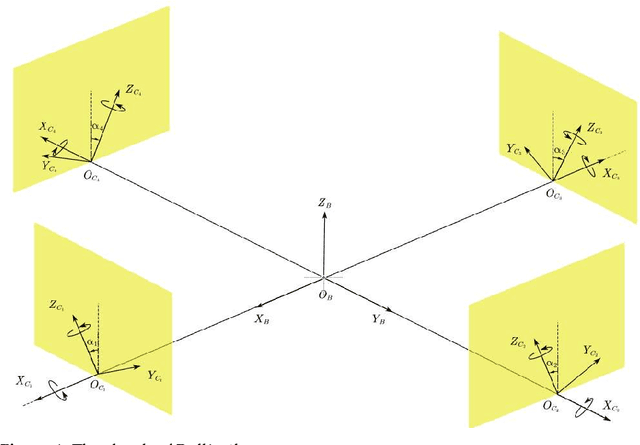
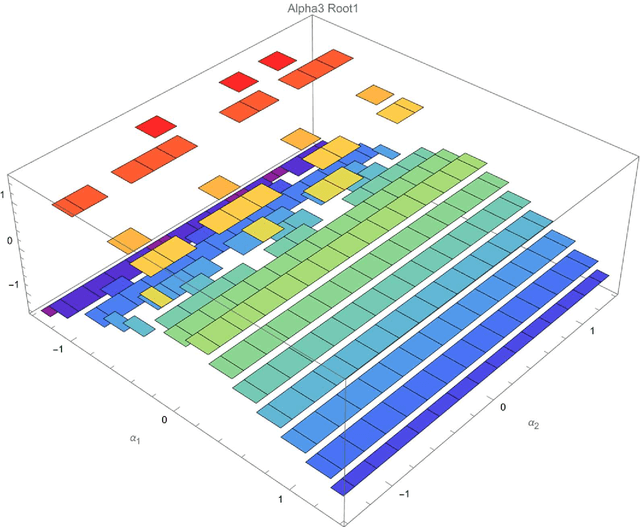
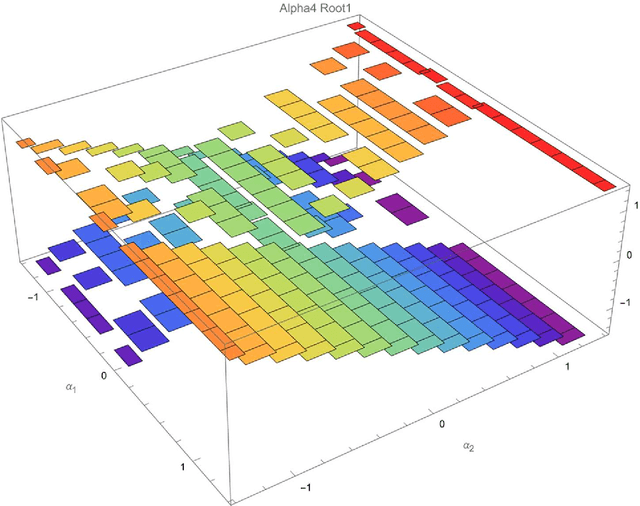
This article presents the four-dimensional surfaces which instruct the gait plan for a tilt-rotor. The previous gaits analyzed in the tilt-rotor research are inspired by animals; no theoretical base backs the robustness of these gaits. This research deduces the gaits by diminishing the effect of the attitude of the tilt-rotor for the first time. Four-dimensional gait surfaces are subsequently found, on which the gaits are expected to be robust to the attitude. These surfaces provide the region where the gait is suggested to be planned. However, a discontinuous region may hinder the gait plan process while utilizing the proposal gait surfaces. A Two Color Map Theorem is then established to guarantee the continuity of each gait designed. The robustness of the typical gaits obeying the Two Color Map Theorem and on the gait surface is demonstrated by comparing the singular curve in attitude with the gaits not on the gait surface. The result shows that the acceptable attitudes enlarge for the gaits on the gait surface.

Feedback Linearization Based Tracking Control of A Tilt-rotor with Cat-trot Gait Plan

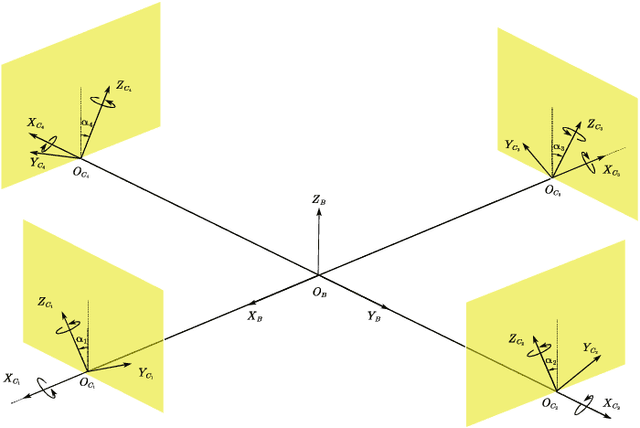
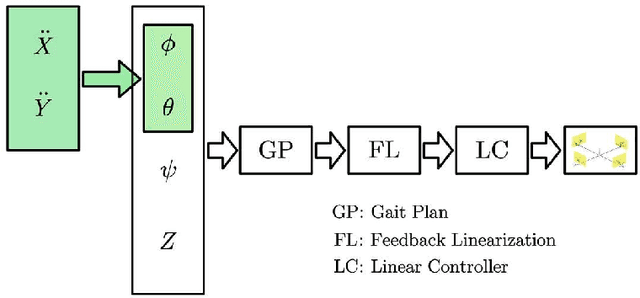
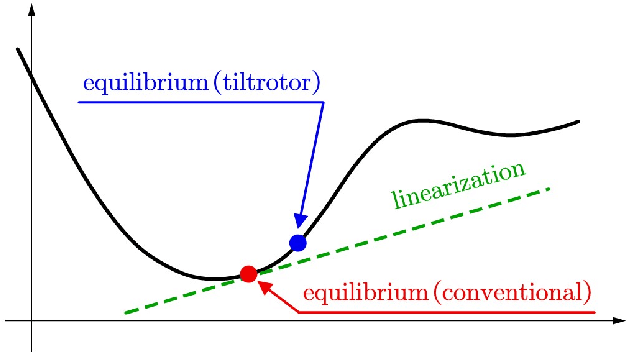
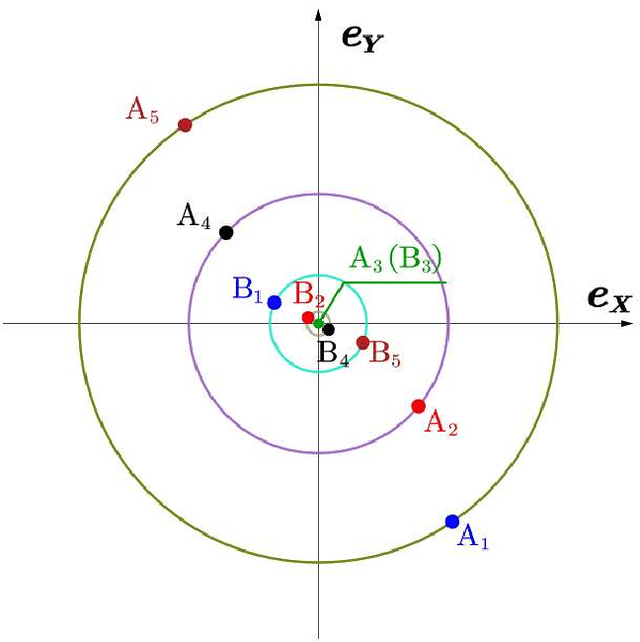
With the introduction of the laterally bounded forces, the tilt-rotor gains more flexibility in the controller design. Typical Feedback Linearization methods of controlling this vehicle utilize all the inputs; the magnitudes as well as the directions of the thrusts are maneuvered simultaneously based on a unified control rule. Although several promising results indicate that these controllers may track the desired complicated trajectories, the tilting angles are required to change relatively fast or in large scale during the flight. This problem challenges the applicability of these control algorithms. The recent idea in sacrifice the number of input and deem the tilt-rotor an under-actuated system may solve this problem; the tilting angles are fixed or vary in a predetermined pattern without being maneuvered by the control algorithm. By careful avoidance of the singular decoupling matrix, several attitudes can be tracked without changing the tilting angles unexpectedly. While the position was not directly regulated by the Feedback Linearization methods in that research, which left the position-tracking still an open question. In this research, we elucidate the coupling relationship between the position and the attitude. Based on this, we design the position-tracking controller adopting Feedback Linearization. We also plan the gait for the tilt-rotor based on the cat-trot gait. The controller is verified in Simulink, MATLAB. Three types of references are designed for our tracking experiments: setpoint, uniform rectilinear motion, and uniform circular motion. The significant improvement with less steady state error is witnessed after equipping with our modified position-attitude decoupler. This steady state error is also influenced by the frequency of the cat-trot gait.

Quad-cone-rotor: A Novel Tilt Quadrotor with Severe-fault-tolerant Ability

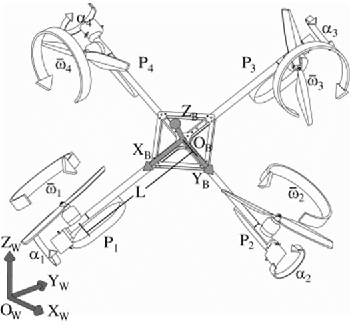
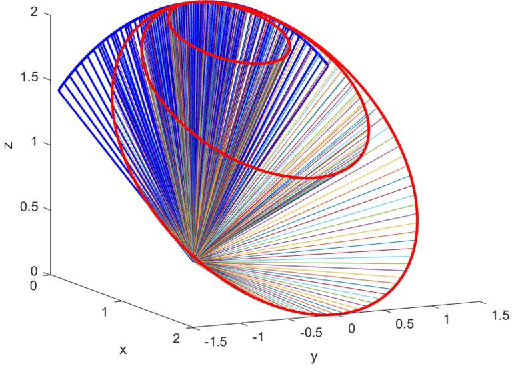
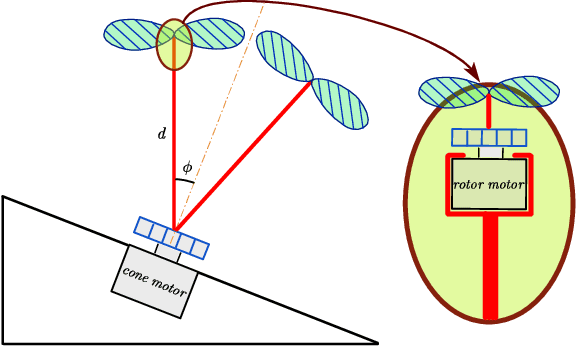
Conventional quadrotors received great attention in trajectory design and fault-tolerant control in these years. The direction of each thrust is perpendicular to the body because of the geometrics in mechanical design. Comparing with the conventional quadrotor, a novel quadrotor named quad-tilt-rotor brings better freedom in manipulating the thrust vector. Quad-tilt-rotor augments the additional degrees of freedom in the thrust, providing the possibility of violating the normal direction of the thrust in the conventional quadrotor. This provides the ability of greater agility in control. This paper presents a novel design of a quad-tilt-rotor (quad-cone-rotor) whose thrust can be assigned along the edge of a cone shape. Besides the inheriting merits in agile from quad-tilt-rotor, the quad-cone-rotor is expected to take fault-tolerant control in severe dynamic failure (total loss in all thrusts). We simulate the control result in a UAV simulator in SIMULINK, MATLAB.